[Deep Learning] Chapter12 Transformers1

• Chapter 10에서는 convolution operation 을 사용하여 각 이미지의 패치를 shared parameters로 processing 하는 방법을 공부하였다.

• 본 챕터에서는 Transformer 를 소개함. 원래는 NLP tasks 를 위한 모델임. Language datasets은 사실 이미지 datasets의 특성과 맞물리는 부분이 있다. 예를 들어, 입력 variable의 dimension 이 크고, 각 포지션마다 확률적 특성이 비슷하다. 또한 각 포지션에서 “dog” 란 단어를 새로 학습할 필요가 없다. (positional invariance)

12.1. Processing Text Data

• Transformer를 이해하기 위해 다음과 같은 예시를 보자

위 예제를 보면 크게 세가지를 알 수 있음.

1. 입력이 너무 커서 FC layer를 쓰기 어렵다.
   • 위 예시에는 37개의 단어로 이루어져있다. 각 단어를 임베딩으로 추출하면 각각 1024의 dimension을 갖는 vector가 되고, $37\times 1024 = 37888$ 이므로 단어 하나가 늘 때마다 입력의 크기가 빠르게 증가함을 알 수 있다.
     보통 입력은 수 백, 수 천 단어의 입력을 가지므로 FC layer를 사용하는 것이 어려울 수 있음. (e.g. 메모리 부족, 긴 연산 시간)
     

2. 입력의 길이가 다를 수 있어서 FC layer 를 쓰기 어렵다.
   • FC layer 를 사용하기 위해서는 정해진 입력, 출력의 크기를 알아야 한다. 하지만 입력의 길이는 매번 달라질 수 있으므로 FC 를 쓰기 어려움

   → 때문에 CNN과 같이 parameters를 share 해야함을 시사한다.

3. text는 모호하다. (e.g. it 이 restaurant 을 의미하는지 vegetarian 을 의미하는지 문맥에 따라 다름.)
   • 사람은 it 이라는 단어가 어떤 단어에 attention 해야하는지 안다.

   → 이는 language model 도 각 단어 사이에 모종의 connection 을 학습해야함을 알 수 있다.

12.2. Dot-Product Self-Attention

앞선 섹션에서 text를 processing 하는 모델은 다음과 같은 특징을 가져야 한다고 하였다.

1. parameter sharing

2. 각 단어 사이의 connections 를 나타낼 수 있어야함.

Transformer 는 앞선 두 가지의 특성을 dot-product self-attention 을 사용함으로 두 마리의 토끼를 잡았다.

self-attention 함수, $\bold{sa}[\bullet]$ 은 $N$개의 embeddings, $\bold{x_1, ..., x_N}$ 을 입력으로 받아 같은 갯수의 vector 들을 출력해야한다. 먼저 values 를 계산해야함. 이는 아래와 같음.

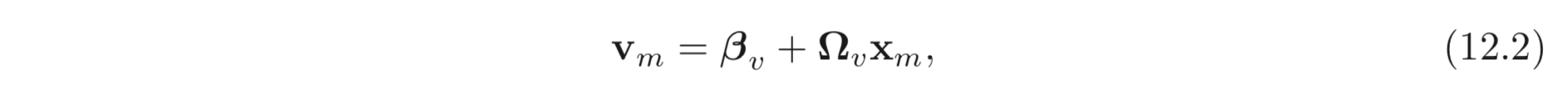
self-attention 의 결과의 $n$번째 row는 다음과 같이 계산된다.

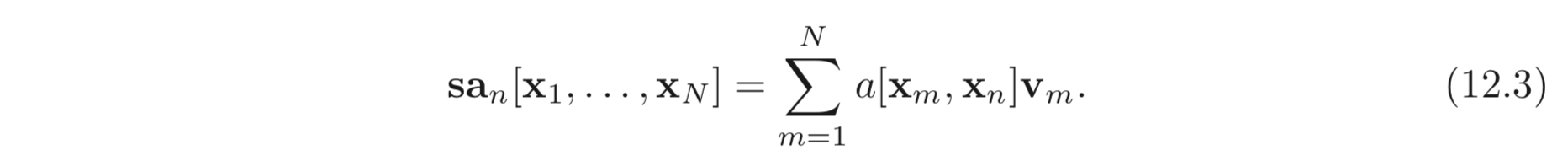
scalar 값, $a[\bold{x}_m, \bold{x}_n]$ 을 attention 이라고 부른다. 이는 n번째 입력 값이 m번째 입력 값에 얼마나 집중하는지를 나타낸다.

12.2.1. Computing and Weighting Values

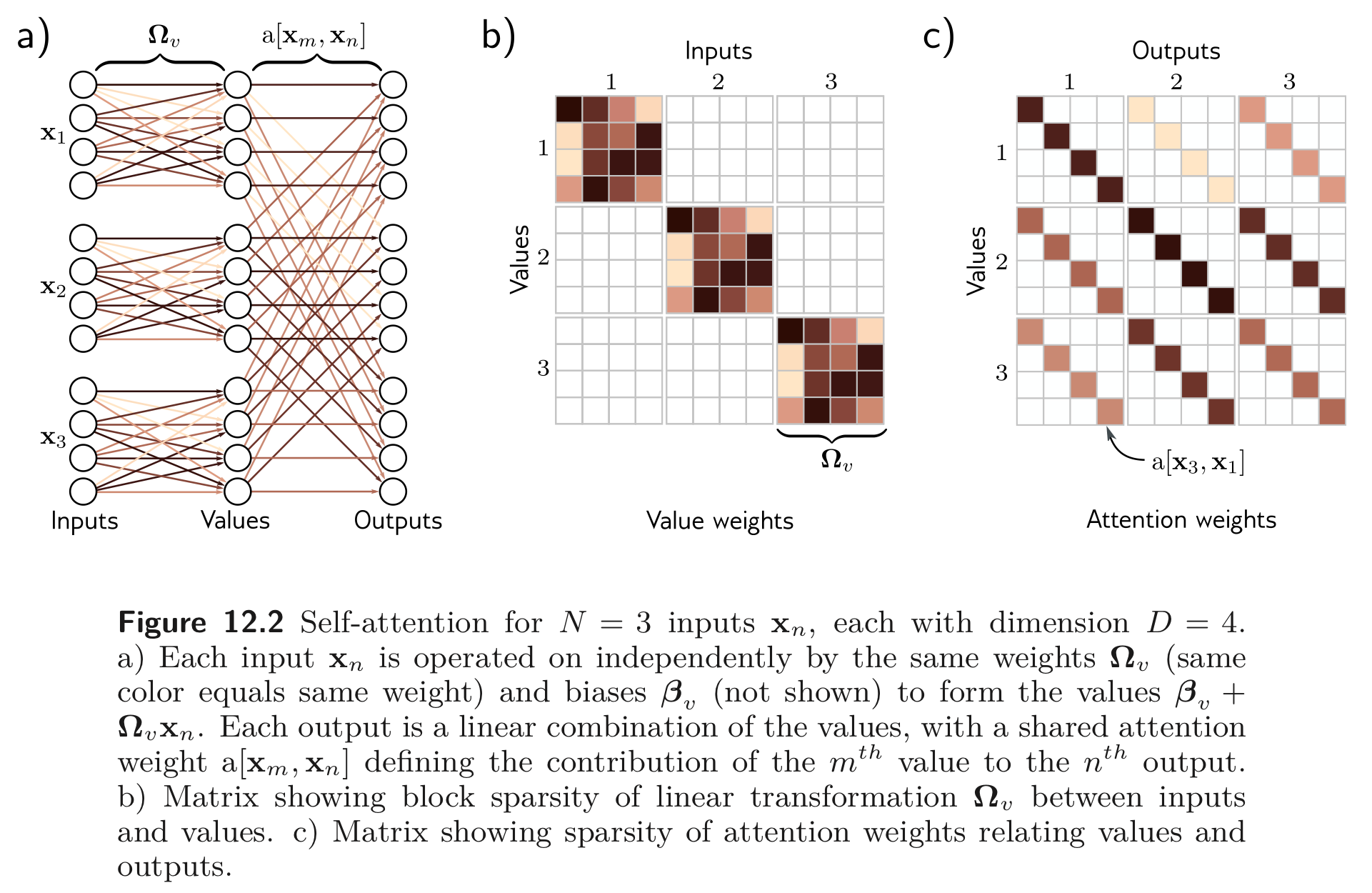
Eq. 12.2 를 보면 하나의 weight, $\bold{\Omega}_v \in \R^{D\times D}$ 와 bias, $\beta$ 를 사용하여 $N$개의 입력 embeddings에 대하여 동일한 연산을 한다. 이는 $DN$ 크기의 matrix를 $DN$ 크기의 출력 matrix 로 mapping 하는 FC layer 보다 더 연산이 적다. self-attention의 values 를 구하는 연산은 shared parameters 를 사용한 sparse matrix operation 으로 볼 수 있다.

12.2.2. Computing Attention Weights

이후 attention weight, $a[\bold{x}_m, \bold{x}_n]$ 들은 $N$ 개의 값에 대하여 각각 곱해진다. 이는 아래와 같이 sparse matrix의 곱으로 표현될 수 있다.

attention 을 계산하기 위해 입력 값에 대하여 두 개의 추가적인 linear transformation 이 필요로하다.

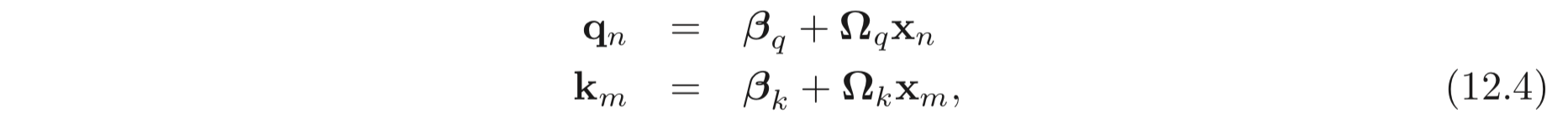
각각의 값들을 queries 와 keys 라고 부른다. 그리고 queries 와 keys 에 대하여 dot-product 을 계산하고 각 값들의 합이 1이 되도록 이를 softmax 함수에 입력으로 준다.

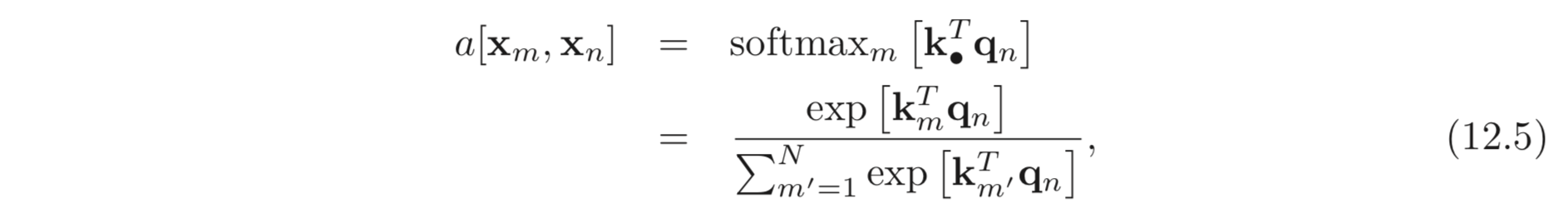
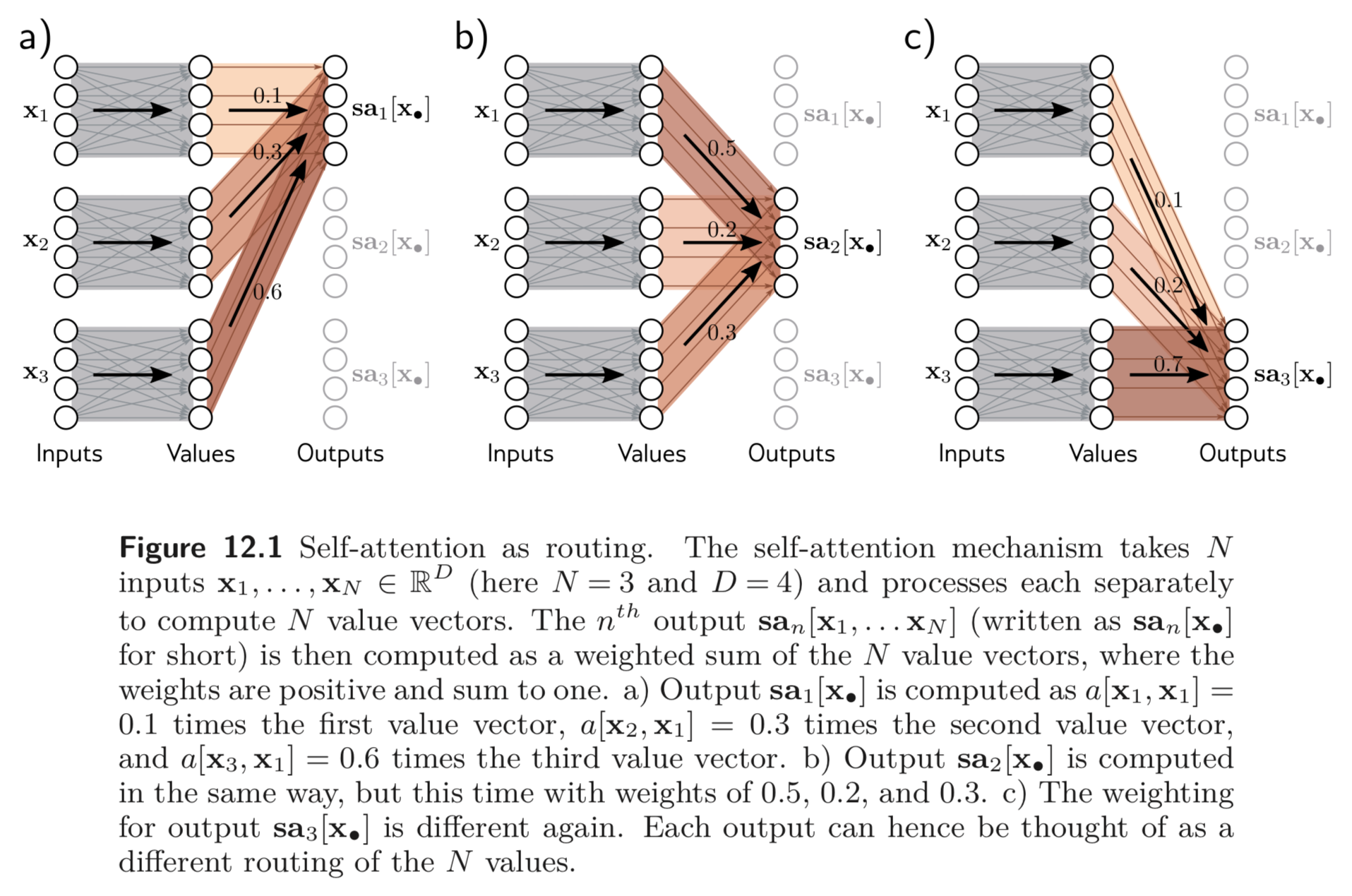
위와 같은 self-attention 방법을 dot-product self-attention 이라고 한다. 이를 하나의 그림으로 나타내면 아래와 같다.

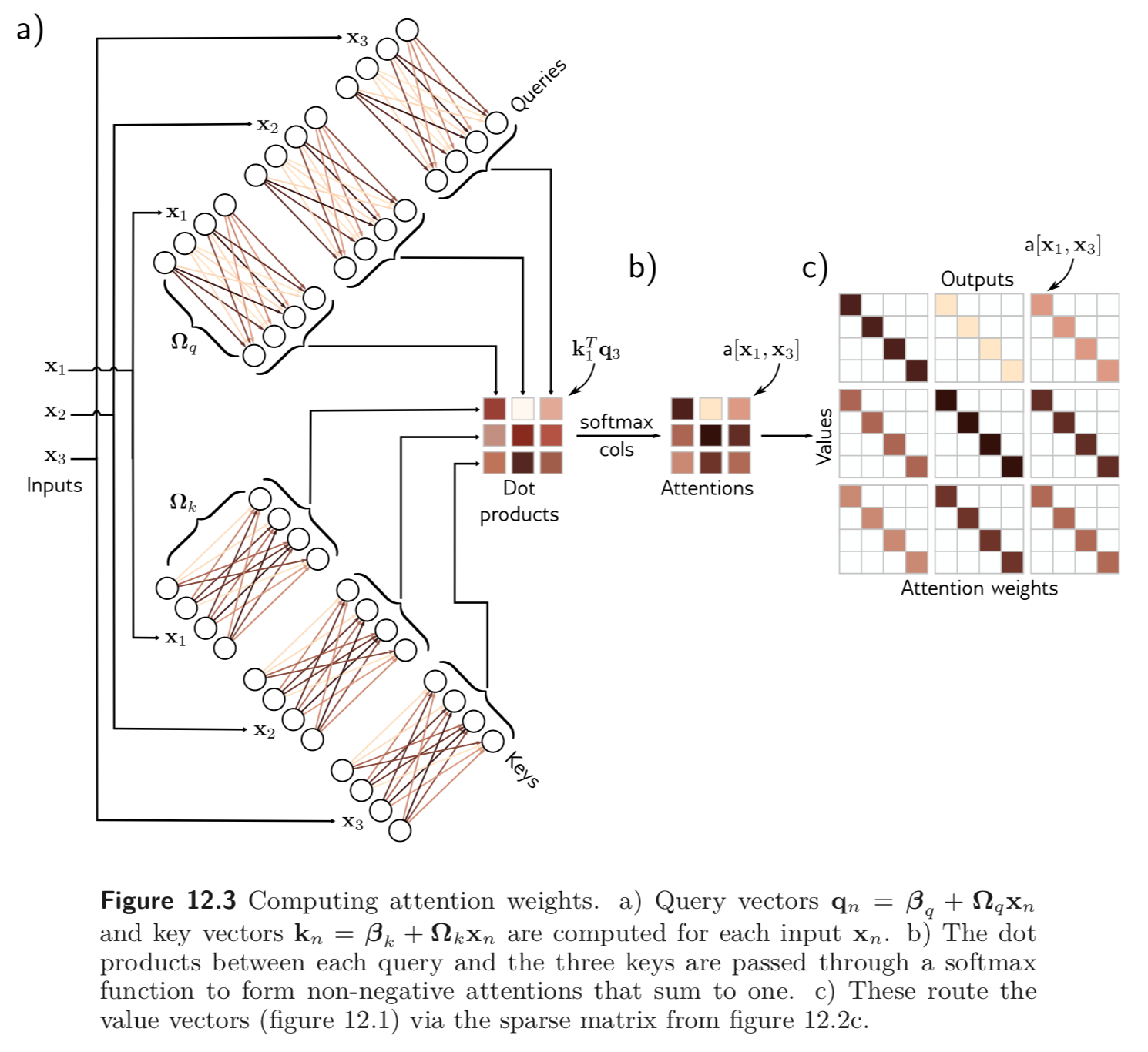
values 와 keys, queries 간의 dimension 의 크기가 서로 달라도 괜찮지만 representation 이 달라지지 않도록 보통 values, keys, queries 모두 같은 dimension 을 갖도록 한다.

12.2.3. Self-attention Summary

self-attention 의 $n^{th}$ output 은 동일한 linear transformation, $\bold{v}_{\bullet} = \beta_v + \bold{\Omega}_v\bold{x}_{\bullet}$ 이 적용된 모든 입력에 모든 값이 양수이고 더하여 1인 weight, attention 값들을 곱한 weighted sum 이다.

$n^{th}$ attention 은 모든 입력 값과 $\bold{x}_n$ 사이의 similarity 값이다. self-attention 연산에는 activation function 이 없지만 dot-product 와 softmax 함수 등의 non-linear 함수가 있어 non-linearity 를 보장할 수 있다.

self-attention 연산을 위해서는 파라미터, $\phi = \{ \beta_v, \bold{\Omega}_v, \beta_q, \bold{\Omega}_q, \beta_k, \bold{\Omega}_k \}$ 를 초기화 해야한다. 이는 $N$개의 입력에 대하여 independent 하여 길이가 다른 입력에 대하여 계산을 수행할 수 있다.

12.2.4. Matrix Form

위와 같은 self-attention 연산을 matrix form 으로 compact 하게 나타낼 수 있다.

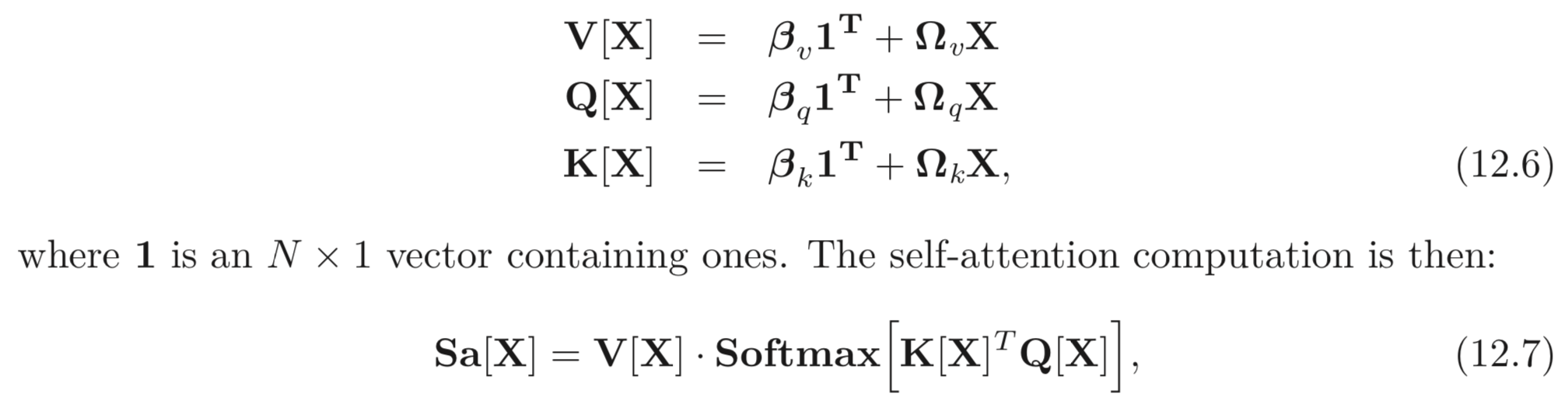
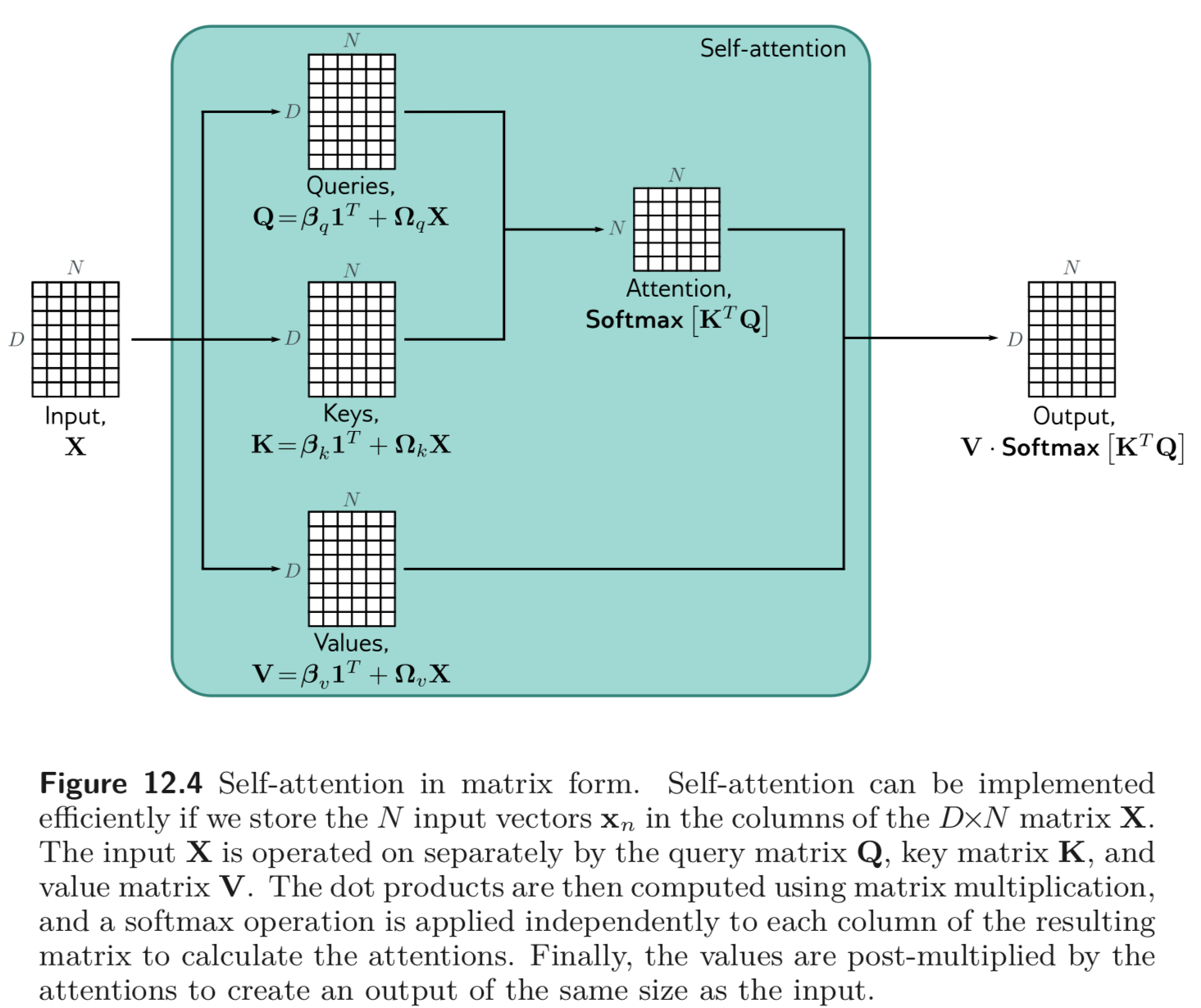
softmax 함수, $\bold{Softmax}[\bullet]$ 함수는 각 columns 에 대하여 적용한다.

12.3. Extentions to Dot-product Self-attention

위 섹션에서 self-attention을 공부함. 본 섹션에서는 실제로 거의 항상 사용되는 3가지 extenstions 에 대해서 공부함.

12.3.1. Positional Encoding

관찰력이 좋은 독자들은 self-attention 메커니즘이 중요한 정보를 빼먹었다는 것을 알아차릴 것임. 바로, 입력, $\bold{x}_n$ 의 “순서”에 상관 없이 모두 같은 연산을 적용 한다는 점이다. 구체적으로는 input permutations에 대하여 invariant 하다고 볼 수 있다.

하지만 “순서”는 중요하다. “The woman ate the raccoon” 과 “The raccoon ate the woman” 은 천지 차이로 다른 의미를 갖는다. 이러한 positional information 을 통합하는 방법에는 크게 두 가지가 있다.

• Absolute positional encodings

  positional information 을 인코딩한 matrix, $\Pi$ 를 input, $\bold{X}$ 에 더하는 것이다. $\bold{\Pi}$ 의 각 colum 은 unique 하다. 따라서 input sequence 의 absolute position 에 대한 정보를 담는다고 할 수 있다.

  $\bold{\Pi}$ 는 입력에만 더해질 수도, 혹은 각 layer 에서 마다 더해질 수도 있다. key 나 query 에도 더해지는 경우가 종종 있으나 values 에는 더하지 않는다.

• Relative positional encodings

  self-attention 의 입력은 여러 문장이 될 수도, 하나의 문장이거나 혹은 문장의 일부 일 수 있다. 따라서 어떤 “word”의 absolute position은 relative position 보다 중요하지 않을 수 있다.

  (예를 들어, 셰익스피어 소설의 10번째 문장의 “Tom” 과 “Amy” 간의 관계와 1번째 문장의 “Tom” 과 “Amy” 간의 관계가 서로 다를까?)

  물론 시스템이 absolute position을 알고 있다면 relative position을 구하는 것도 어렵지 않지만 relative positional encoding은 이를 “직접”한다.

  attention matrix의 각 값들은 query potision, $a$ 와 key position, $b$에 대응된다. Relative positional encodings 는 이러한 값, $\Pi_{a,b}$ 를 학습하여 입력에 더하거나 곱하는 등의 연산을 수행한다.

12.3.2. Scaled dot product self-attention

attention 메커니즘에서 dot products의 결과로 출력 값이 아주 큰 값을 가질 수 있다. 그리고 이 출력값을 가장 큰 값 만이 dominant한 (softmax 는 one-hot encoding의 smooth version) softmax 연산에 입력으로 들어간다. 결과적으로 입력 값에서의 작은 변화는 출력 값에 영향을 거의 주지 못하게 (e.g. gradient 가 아주 작게 계산됨.) 되어 학습에 지장을 준다.

이를 방지하기 위해 dot products의 출력 값에 $\sqrt{D_{key\space or\space query}}$ 를 나누어준다. ($D_{key\space or\space query}$ 는 key 혹은 query 에 입력으로 들어가는 vector의 dimension이다.) 이는 아래와 같이 계산된다.

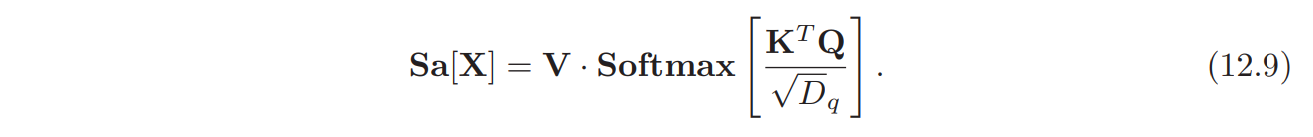
이를 scaled dot product self-attention 이라고 한다.

12.3.3. Multiple Heads

Multiple self-attention 메커니즘은 주로 parallel 하게 적용되는데, 이를 multi-head self-attention 이라고 한다. $H$ 개의 서로 다른 values, keys and queries의 set이 존재하고 아래와 같이 연산된다.

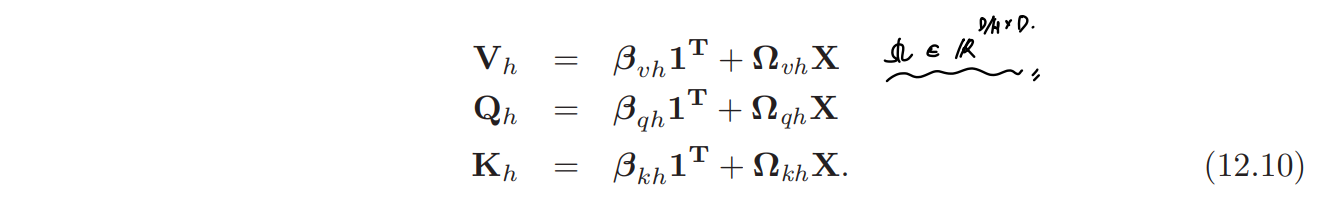
$h^{th}$ self-attention 혹은 $head$ 는 아래와 같이 계산될 수 있다.

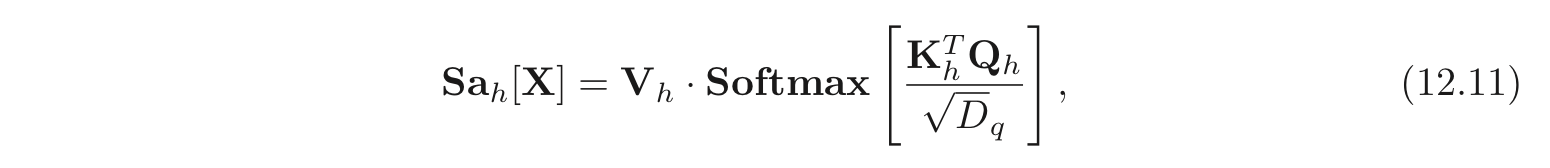
각각의 $head$는 각각의 $V, Q, K$ 를 계산하는 파라미터를 가진다. 보통 $m$번째 input, $\bold{x}_m$ 의 dimension 이 $D$ 이고, $H$개의 head가 있다면, 효율적인 연산의 구현을 위해 $V, Q, K$를 계산하는 각각의 파라미터들의 row의 크기를 $\frac{D}{H}$ 로 통일시킨다.

각 head의 output은 vertically concatenated 되고 다른 linear transform, $\bold{\Omega}_c$ 를 곱하여 각 output 들을 combine 한다. (See Fig. 12.6)

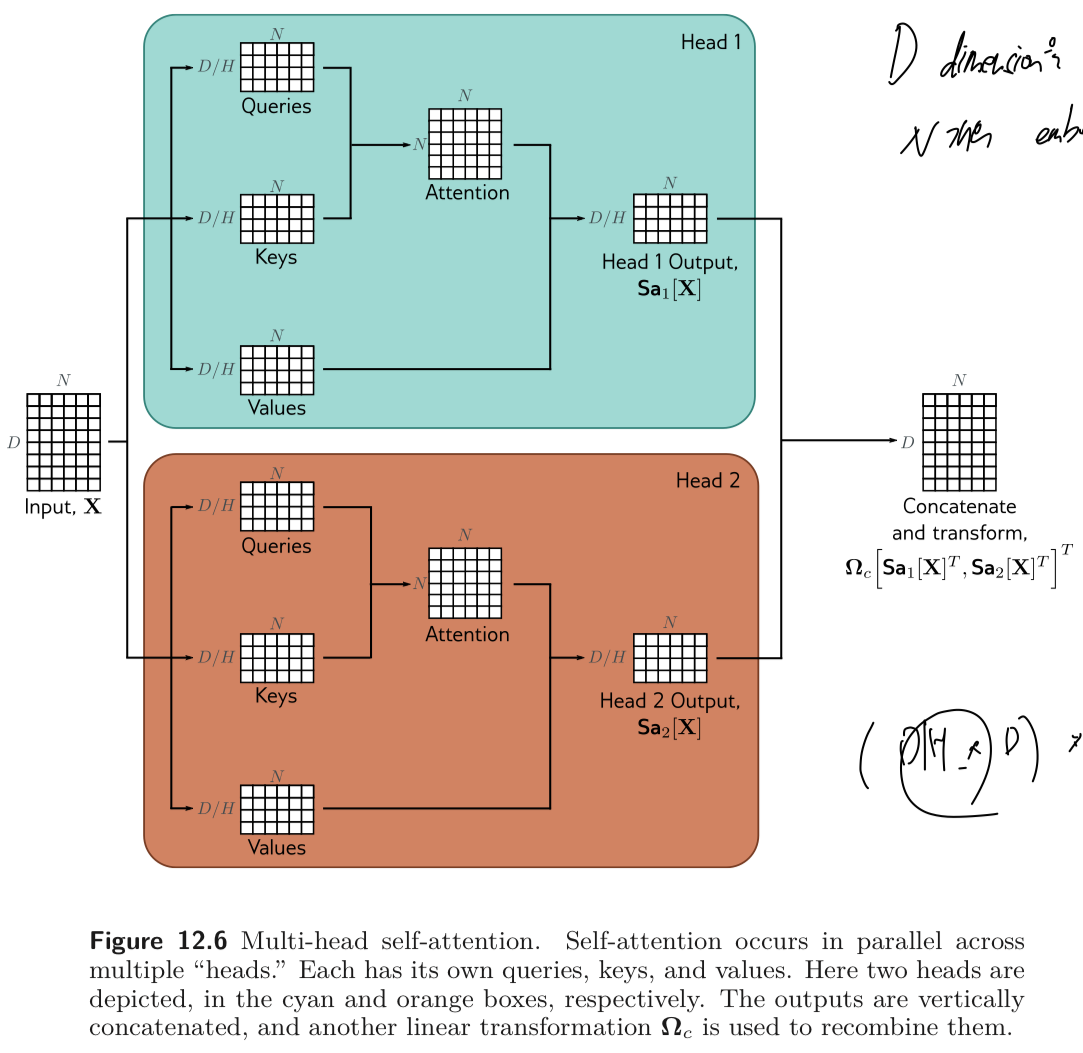
multi-head self-attention 을 수식으로 나타내면 아래와 같다.

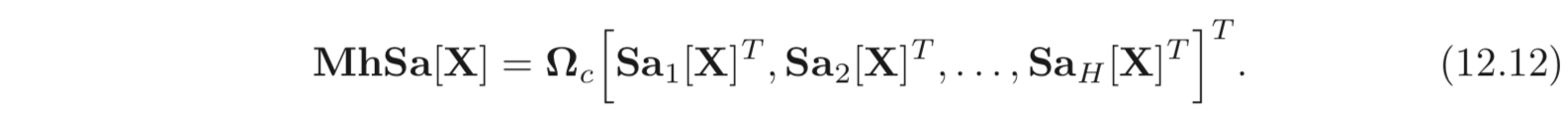
multi-head attention 은 transformer가 잘 동작하기 위해 필요하다고 보임. 이는 self-attention network 를 bad initialization 에 대해서 더 robust 하게 만들어준다고 여겨진다.

(Attention matrix 를 하나만 구하는 것이 아니라 여러 개를 구하기 때문에 앙상블의 효과도 있을 것이라고 생각됨.)

12.4. Transformers

Self-attention 은 큰 transformer 구조의 일 부분이다. Transformer 는 multi head self-attention unit (words의 서로 간의 관계를 계산.) 뒤에 FC layer unit (각 words 에 대하여 어떤 transform 을 연산함.) 이 따라 붙는 구조를 갖는다.

두 units 는 residual network 이고 보통 각 unit 뒤에 LayerNorm 연산이 따라 붙는다. LayerNorm 은 BatchNorm 과 비슷하지만 각 tokens 들에 대하여 statistics를 사용한다는 점이 다르다. 이는 Eq. 12.13 과 같은 수식, Fig. 12.7 과 같이 표현할 수 있다.

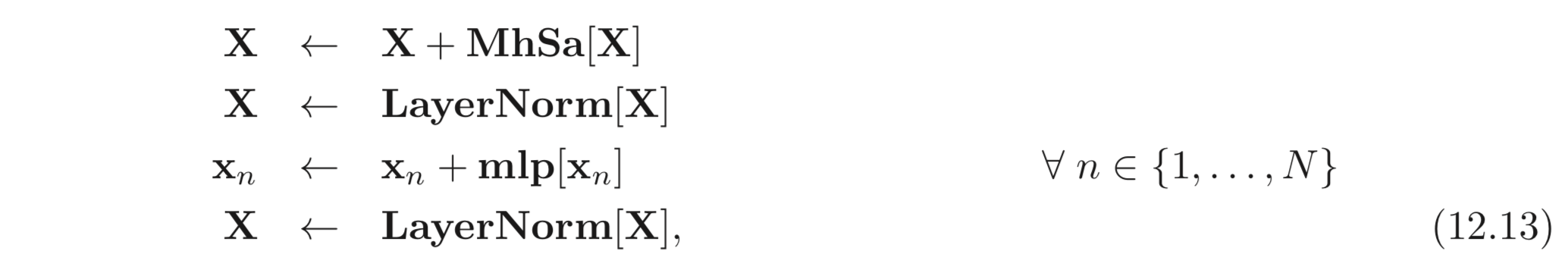
$\bold{x}_n$ 은 전체 input, $\bold{X}$ 에서 뽑아낸 하나의 vector 이다. ($\bold{x}_n \in \bold{X}$). 실제 네트워크는 이러한 연산을 여러번 반복한다.

Uploaded by N2T