[Deep Learning] Chapter11 Residual Networks

• Chapter 10에서는 CNN에 대하여 공부하고 그 중에서도 AlexNet, VGGNet과 같은 traditional CNN을 살펴보았다. 여기서 AlexNet은 8개의 layers를 가졌고, VGGNet은 18개의 layers를 가졌는데 VGGNet이 더 좋은 성능을 보여 Deeper networks가 더 나은 성능을 기대할 수 있다고 보았다.
  
  하지만, 더 많은 훨씬 더 많은 layer를 추가하자 오히려 다시 성능이 감소하는 현상을 관측하였다.

• 본 챕터에서는 network를 더욱 deeper하게 설계할 수 있는 기술인 residual connection (skip connection) 과 batch normalization 에 대하여 공부한다.

• Residual connection과 batch normalization을 같이 사용하여 모델을 더욱 깊게 설계할 수 있음을 보인다. 또한 이를 활용한 U-Net, Hourglass structure 도 예시로 살펴본다.

11.1 Sequential Processing

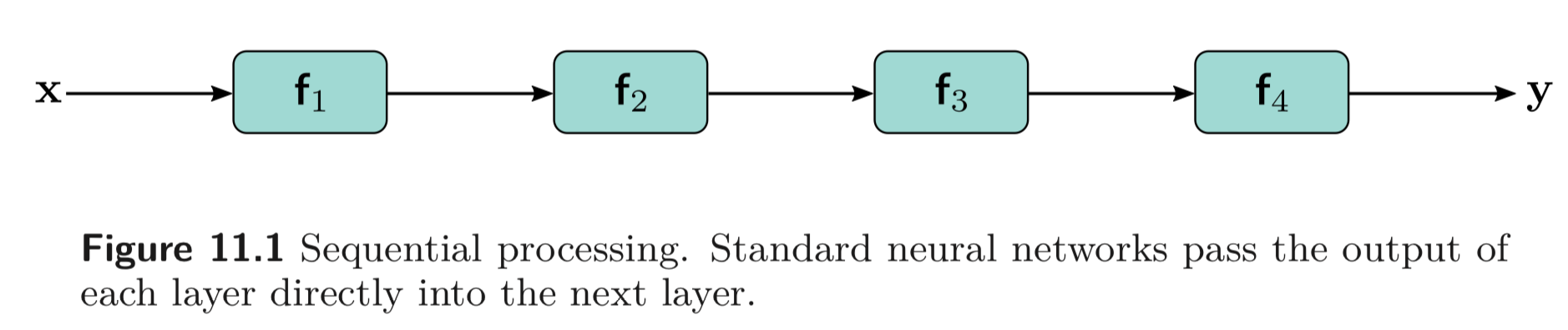
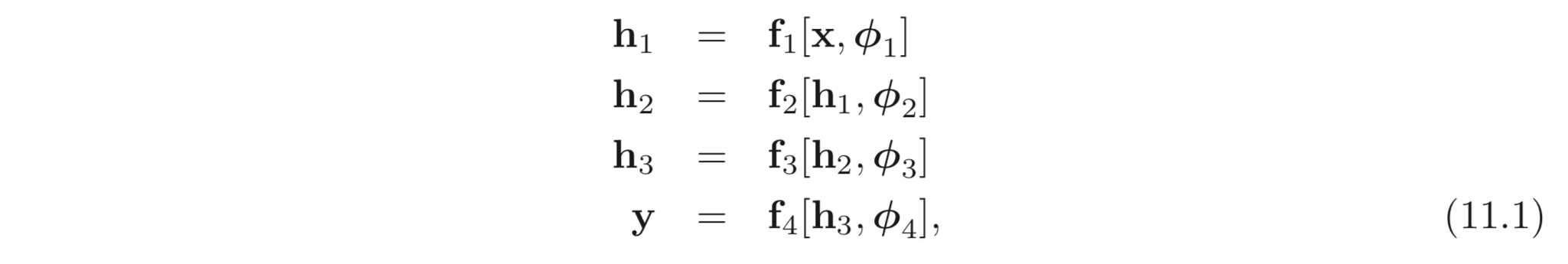
지금까지 봐왔던 networks들은 모두 Fig. 11와 Eq. 11.1 와 같이 sequential 하게 연산하였다.

11.1.1 Limitation of Sequential Processing

우리는 원한다면 얼마든지 layer를 많이 쌓아 정말 deep한 모델을 설계할 수 있다. 과 VGGNet (18 layers) 이 AlexNet (8 layers) 보다 좋은 성능을 낸 것처럼, deeper한 모델은 또한 더 좋은 성능을 낼 것이라고 기대할 수 있다.

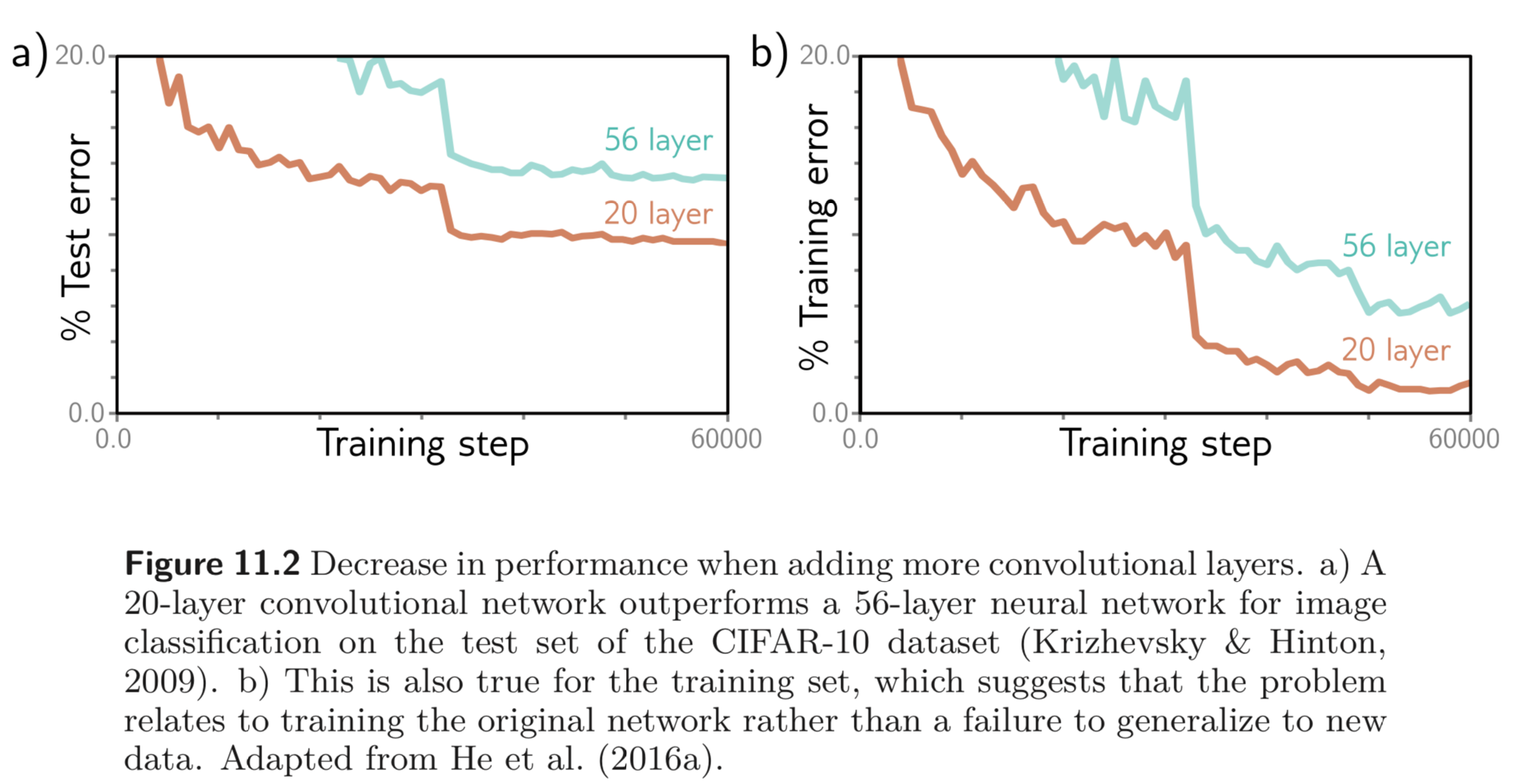
하지만 Fig. 11.2에서 보이는 실험은 오히려 layer를 깊게 쌓았을 때 (56 layers) 얕게 쌓은 모델 (20 layers) 보다 training, test 모두 에서 더 안좋은 성능을 보임을 볼 수 있다.

이러한 현상의 원인은 아직 명확히 밝혀지지 않았다. 한가지 추측은 initialization 단계에서, 모델의 early layers의 parameters를 update 할 때 loss gradients 가 예측 불가하게 변하기 때문이라고 볼 수 있다. 앞서 He initialization 과 같은 방법으로 parameters를 적절히 initialize 하면 하지 않았을 때보다 gradient 의 변화가 그렇게 심하지 않다.

하지만, Gradient descent와 같은 finite 한 step의 크기를 갖는 optimization algorithm과 달리, 실제 gradient는 parameters의 infinitesimal 한 구간 ($\Delta x \rightarrow 0$) 에서의 기울기를 구한 것이다. 아무리 step size 를 잘 선택하더라도 loss surface가 step size 보다 작은 공간에서 변동성이 크다면, update 된 parameters 는 전혀 엉뚱한 곳에 도달할 수도 있다.

early layers에서의 gradient 가 예측 불가능하게 변해서 모델이 깊어질 수 없다는 가정은 하나의 레이어를 갖는 모델을 가지고 이를 뒷받침 할 수 있다.

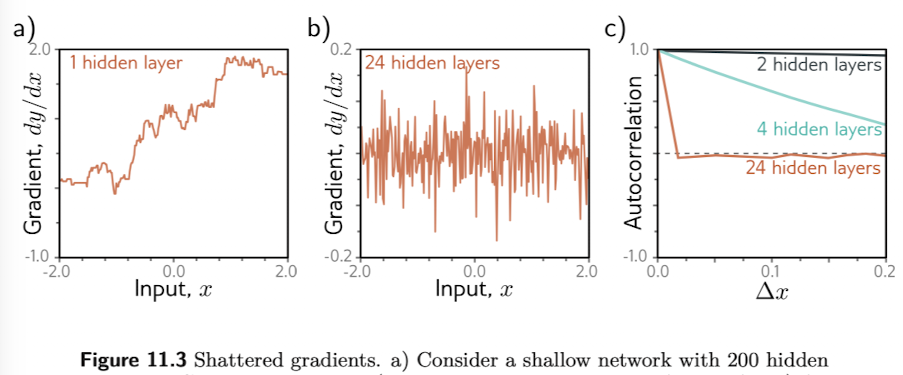
Fig. 11.3a) 은 하나의 레이어를 갖는 모델의 각 x값에 대한 gradient 이다. $x$의 값에 따라 gradient 의 변동성이 크지 않다. (각 $x$ 에서의 기울기를 보면됨.). 반면, Fig. 11.3b)에서는 24개의 레이어를 갖는 상대적으로 깊은 네트워크는 $x$가 변함에 따라 gradient가 예측 불가하게 변하는 것을 볼 수 있다. ($x$의 작은 변화에도 gradient 가 큰 폭으로 변하기 때문에 parameter의 update도 불규칙적으로 될 가능성이 높다고 볼 수 있을 것 같다.)

이러한 gradient들의 변화의 autocorrelation 을 구하면 Fig. 11.3c) 와 같이 구해볼 수 있다. layer가 깊어질 수록 $\Delta x$ 가 아주 작을 때만 autocorrelation 값이 큰 것을 볼 수 있다. 이러한 현상을 shattered gradients phenomenon 이라고 한다.

Shattered gradient 는 모델이 깊어질 수롣 early layers의 변화가 output을 굉장히 복잡한 방법으로 계산하기 때문에 발생한다고 볼 수 있다.

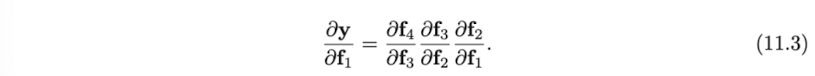
Eq. 11.3 에서는 $\bold{f_1}$ 의 gradient 를 계산하기 위해서는 $\bold{f_2, f_3, f_4}$ 의 gradient 를 chain rule 에 따라 순차적으로 곱해야한다는 것을 볼 수 있다. 따라서 $\bold{f_1}$ 에 영향을 주는 parameter 를 update 하면 $\bold{f_2, f_3, f_4}$ 에도 영향을 줄 수 밖에 없다. 결과적으로 매 training example 에 대하여 구한 gradient 가 굉장히 messy 할 수 밖에 없을 것이다.

11.2 Residual connections and Residual blocks

Residual 혹은 Skip connection 은 input이 각 네트워크 레이어, $\bold{f[\bullet]}$ 의 output 에 다시 더해지는 계산 경로에서의 branches 를 말한다. (See Fig. 11.4a))

Figure 11.4a) Residual connections

수식적으로는 아래와 같이 나타낼 수 있다.

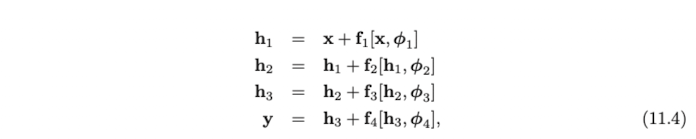
우항의 식들은 벡터들의 합을 의미하므로 입력과 결과의 shape이 같아야함을 알 수 있다. 이와 같은 input과 output의 덧셈으로 이루어진 block을 residual block 혹은 residual layer 라고 한다.

위 식에서 마지막 식 ($\bold{y} = \bold{h_3} + \bold{f_4}[\bold{h_3}, \phi_4]$) 을 하나하나 풀어서 쓴다면 이를 아래와 같이 나타낼 수 있다. ($\phi$들은 생략.)

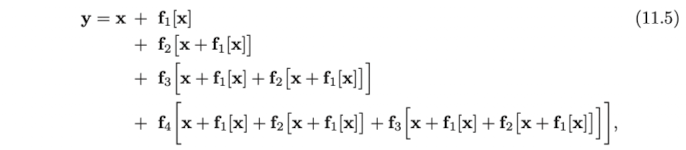
결국 최종 식은 input과 각 layers, $\bold{f_1, f_2, f_3, f_4}$ 의 output의 합으로 풀어해쳐졌다고 볼 수 있다. (See Fig.11.4b). 따라서 residual network는 하나의 network를 작은 networks 들로 나누어 이들의 합이 최종 결과가 되게 하는 하나의 ensemble 모델로도 볼 수 있다.

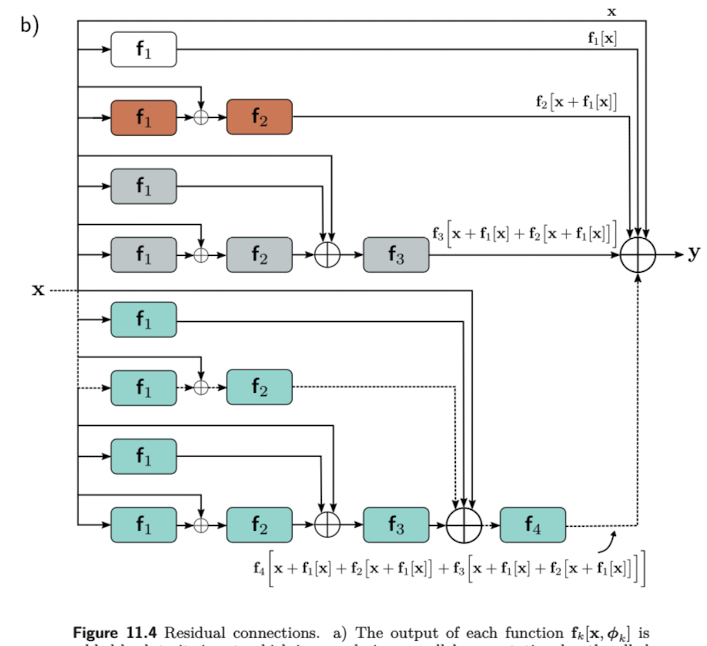
추가적으로 residual connection 은 아래와 같이 input에서 output으로 연결되는 추가적인 connection을 만든다. (본 예제에서는 총 16개의 path가 생김.) 앞서 early layer 들의 변화가 이후에 따라오는 layer들의 영향을 주기 때문에 gradient가 예측하기 어렵게 변동성이 크다는 추측을 하였다. 따라서 layer가 얕을 수록 “좋은” gradient 가 계산된다고 볼 수 있다.

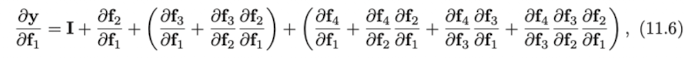
Coming soon..

Uploaded by N2T