[Deep Learning] Chapter7 Gradients and Initialization

Take Home

Priliminaries

Abstract

7.1 Problem Definitions

7.2 Computing Derivatives

7.3 Toy Example

7.4 Backpropagation Algorithm

7.4.1. Backpropagation Algorithm Summary

7.4.2. Algorithmic Differentiation

7.5. Parameter Initialization

7.5.1. He Initialization (ReLU 를 쓴다면 이 initialization 을 쓰세요)

7.5.3. Initialization for both forward and backward pass

Take Home

1. Backpropagation Algorithm이 어떻게 동작하는지에 대한 이해
   • Forward Pass 에서 결과값을 계산하고 저장함.
   • Backward Pass 에서는 저장된 결과값을 chain rule 에 따라 아래와 같이 계산.

     

     ( ) 괄호 쳐진 부분은 Backward pass 에서 앞서 계산된 값들임. 따라서 괄호 밖에 있는 값들만 계산한다.

2. Parameter Initialization 은 학습이 안정적으로 되기 위해서 각 파라미터들이의 결과들이 비슷한 분포를 갖도록 초기화하는 방법임.

   

   Fig 7.7. Weight Initialization. 모든 레이어의 D_h 가 100인 경우에 a) 는 forward pass 의 각 layer 별 activations의 크기를, b) 는 backward pass 의 gradients 의 크기를 시각적으로 표현한 것이다. 각 레이어의 weights의 분포가 2/D_h = 0.02 일 때 forward pass, backward pass에서의 activations, gradients 가 안정적으로 유지 되는 것을 볼 수 있다.
   0.02 보다 작으면 vanishing gradient, 0.02 보다 크면 exploding gradient 문제가 발생할 수 있다.
   

   • 학습이 불안정: → vanishing (or exploding) gradients problem
   • 본 교재에서 제안한 방법: He Initialization

     

Priliminaries

• chain rule

• calaulation derivatives of vector and matrix

Abstract

이전에 Chatper 6 에서 iterative optimization algorithms 들을 공부하였다. 이들은 어떤 function의 최소값을 찾는 범용적인 접근법들이다. Neutral network의 관점에서는 input이 주어졌을 때 정확한 output을 예측하도록 loss를 최소화하는 파라미터를 찾는 것으로 볼 수 있다. 가장 기본적인 방법은 초기 파라미터를 랜덤하게 설정하고 loss를 최소화 하는 loss의 현재 파라미터에 대한 미분값, 즉 gradient를 계산한다.

본 챕터에서는 크게 두 가지 이슈를 중점적으로 다룬다.

1. Gradient를 그러면 어떻게 “효율적”으로 계산할 수 있는지?

2. Parameters를 어떻게 initialize 하면 좋을지?

7.1 Problem Definitions

다음과 같은 뉴럴넷, $\bold{f[x, \phi]}$, input, $\bold{x}$, 파라미터, $\phi$와 3개의 hidden layers,$\bold{h_1, h_2, h_3}$ 를 생각해보자.

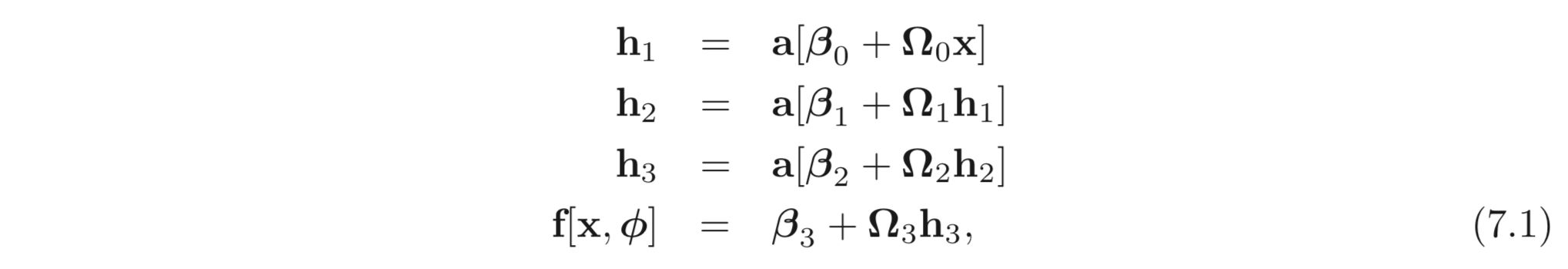
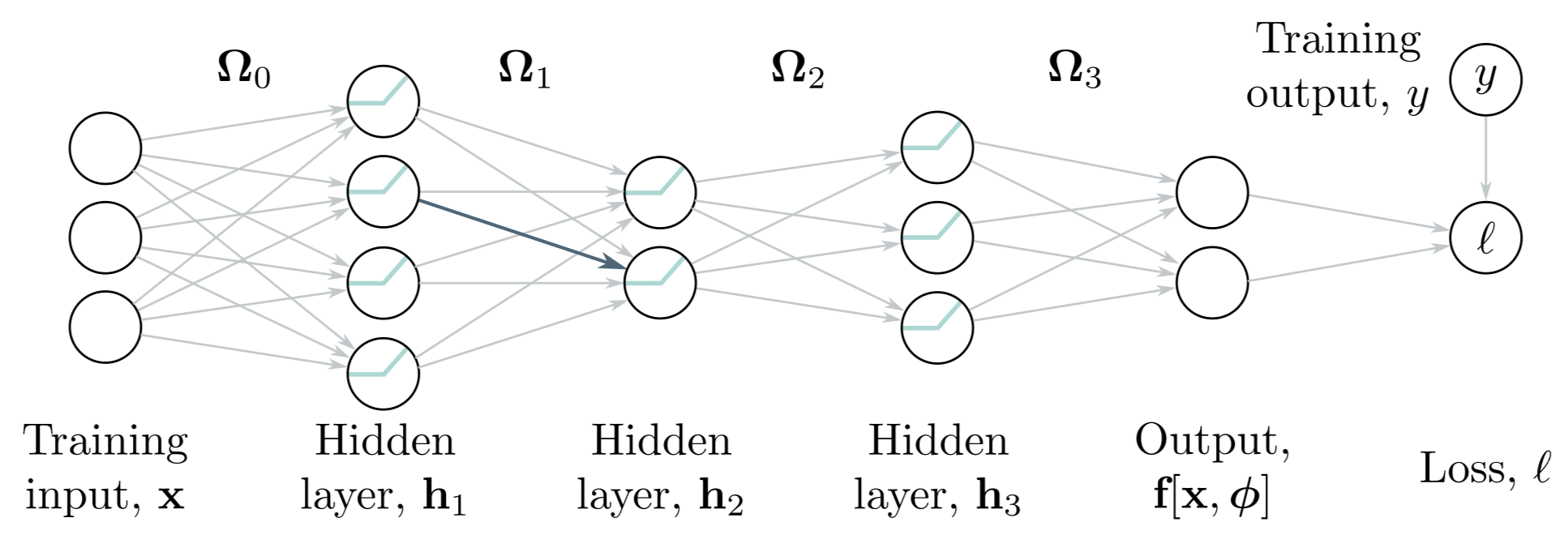
activation function, $\bold{a}[\bullet]$은 element-wisely 연산된다. $\phi = \{\bold{\beta_i, \Omega_i}\}_{i=1}^3$ 으로 정의된다. $\beta$는 vector bias, $\bold{\Omega}$ 는 weight matrix이다. 위 모델을 그림으로 표현하면 아래 Fig 7.1 와 같다.

Fig 7.1 Backpropagation forward pass.

label, $y_i$, prediction, $\bold{f[x_i, \phi]}$ 와의 distance인 $l_i = (f[\bold{x_i, \phi}] - y_i)^2$ 와 같이 $i$번째 데이터에 대한 loss, $l_i$ 를 계산할 수 있을 때 total loss는 아래와 같이 계산된다.

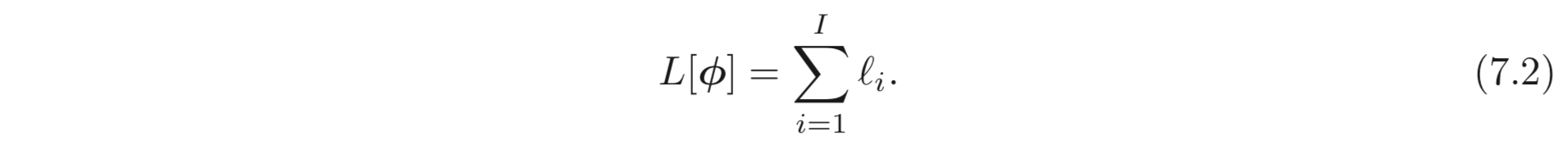
본 챕터에서는 optimization algorithm으로 Stochastic Gradient Descent (SGD)를 사용한다.

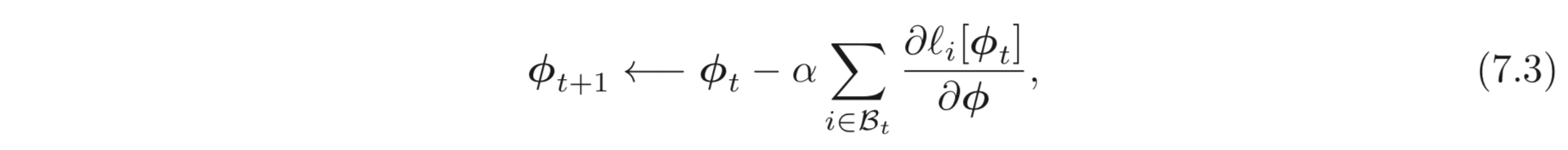
$k$번째 layers의 bias와 weights를 업데이트 하기 위한 gradient는 아래와 같이 계산된다.

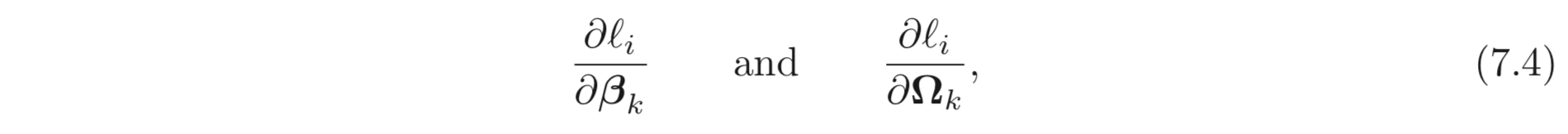
이러한 gradient를 효율적으로 계산하는 방법인 backpropagation algorithm을 먼저 공부한다. 그리고 학습이 안정적으로 이루어질 수 있도록 bias와 weights를 initialize하는 방법에 대해 공부한다.

7.2 Computing Derivatives

derivatives는 파라미터에 변화를 주었을 때 loss가 어떻게 변하는지에 대하여 알려준다. optimization algorithm은 loss가 계속 작아지도록 이러한 정보를 사용하여 파라미터를 업데이트한다. backpropagation algorithm은 이러한 derivatives를 계산하는 알고리즘이다. 수학적인 디테일이 필요하므로 아래와 같은 두 가지 사실을 먼저 보고 간다.

1. Observation 1: input에 매 layers를 지나며 파라미터들의 값이 곱해지고 더해진다. 따라서 아주 작은 파라미터 값의 변화라도 layer를 거치며 그 결과가 증폭되거나 사라질 수 있다, 즉 큰 영향을 미친다. 따라서 이렇게 한 번 계산한 값들을 버리지 않고 backward를 위해 저장해준다. 이러한 과정을 forward pass 라고 한다. (Fig 7.1을 보라)

2. Observation 2: bias나 weight의 작은 변화도 그 다음 네트워크에 도미노 처럼 효과를 줄 수도 있다. 이러한 변화는 다음 레이어에 영향을 주고 또 그 다음 레이어에도 영향을 준다. 결국 여러 레이어를 모두 거쳐 loss에 까지 영향을 준다. 따라서 어떤 파라미터 하나의 변화가 loss에 어떤 영향을 미쳤는지를 알기 위해서는 해당 파라미터와 관련 있는 모든 파라미터들의 영향도 고려해야한다. (Fig 7.2)

Fig 7.2 Backpropagation backward pass

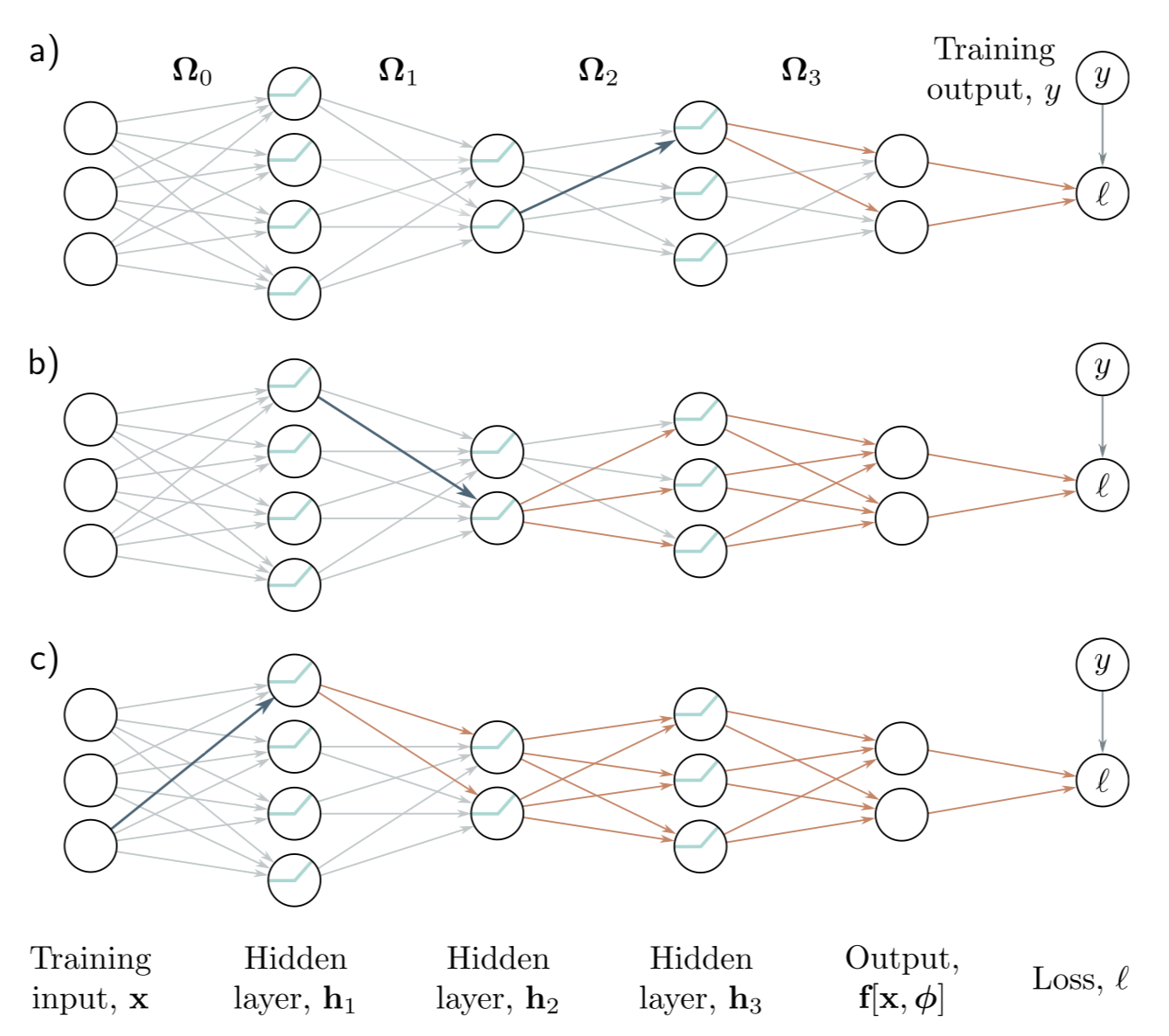
앞서 계산된 activations들의 값을 한 번 계산하고 저장해두면 이후 이와 연관된 다른 파라미터의 gradient를 계산할 때 효율적인 계산에 도움이 될 수 있다.

이와 같이 network의 뒤로 갈 수록 대부분의 파라미터에서 계산될 값들이 앞선 step인 forward pass에서 계산이 되었다. 따라서 backward pass에서는 이들의 값을 다시 계산할 필요가 없다. 이러한 방법으로 derivatives를 계산하는 것을 backward pass라고 한다.

이제는 수학적으로 파보자.

7.3 Toy Example

8개의 파라미터, $\phi=\{\beta_0, \omega_0, \beta_1, \omega_1, \beta_2, \omega_2, \beta_3, \omega_3\}$를 갖는 model, $f[x, \phi]$를 다음과 같이 정의한다.

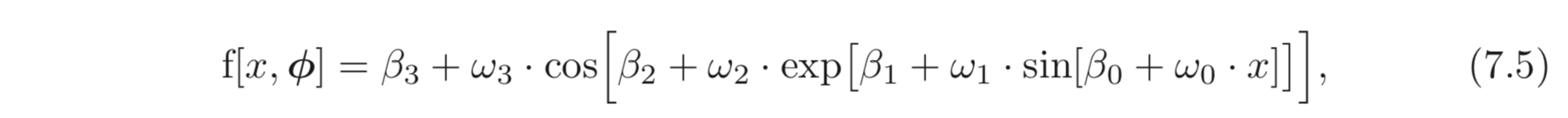
loss는 MES Loss로 한다. $i$번째 데이터 pair, $\{x_i, y_i\}$ 에 대한 loss는 $l_i = (f[x_i, \phi]-y_i)^2$ 으로 정의한다. 따라서 우리는 아래 식과 같이 $l_i$에 대한 각 파라미터들의 derivatives를 구하는 것이 목표이다.

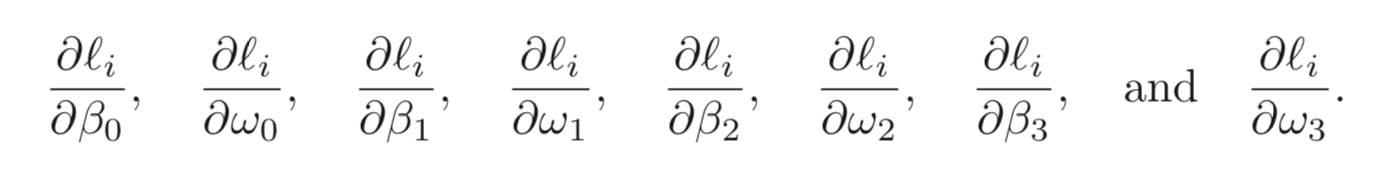
물론 주어진 간단한 식의 경우 각 파라미터에 대한 graident를 직접 손으로 구해볼 수도 있으나 파라미터가 수백억개도 넘어가는 현대의 딥러닝 모델에는 적용하기 어려울 것이다. 아래는 $\omega_0$ 에 대한 $l_i$의 derivative를 직접 구한 예시이다.

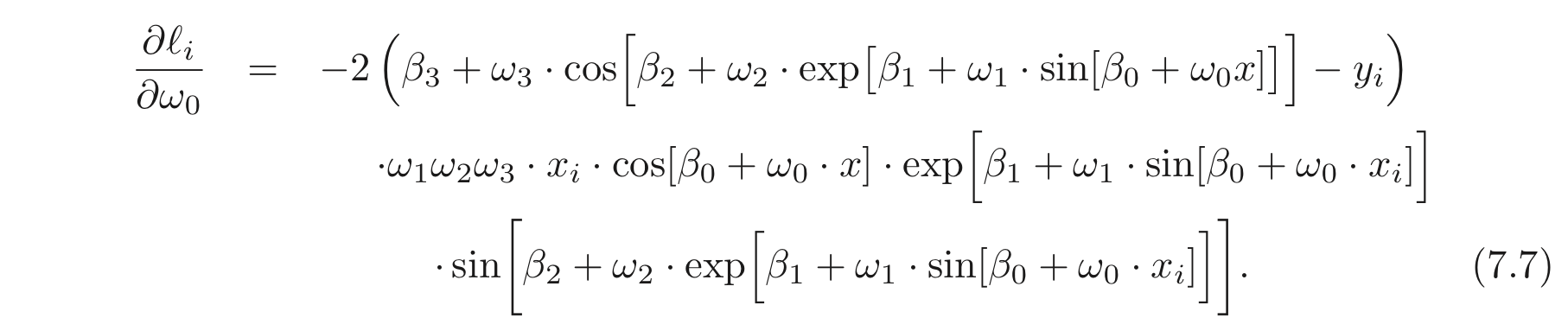
이는 계산하기도 난해할 뿐더러 코딩하기도 만만치 않다.

반면, backpropagation algorithm은 앞서 구하고자하는 모든 derivatives를 한번에 계산하기 위한 알고리즘이다. 이는 다음과 같은 두 가지를 포함한다. (1) forward pass: 일련의 networks의 output과 intermediate을 계산하고 저장한다. (2) backward pass: 각 파라미터의 derivatives를 계산하며 network의 “끝” (loss) 에서 시작하여 “앞” (input) 으로 가는데 이때 forward pass에서 계산한 값들을 재사용한다.

Forward pass: loss를 계산함을 연속된 계산들로 여긴다.

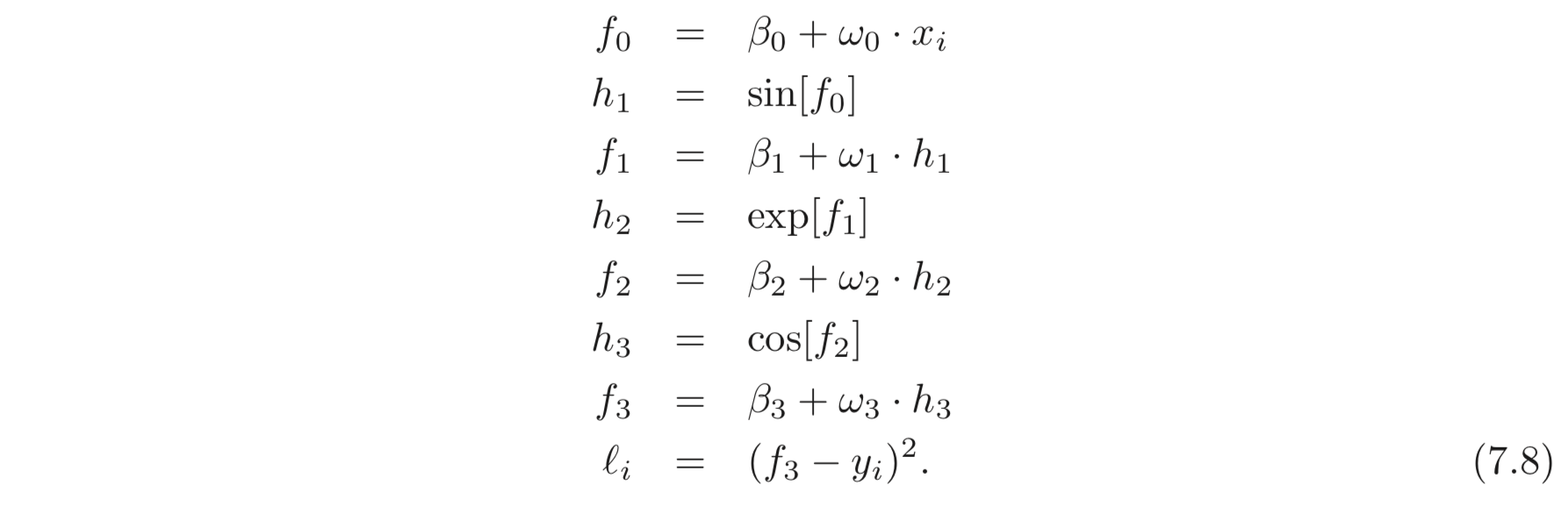
$f_k, h_k$ 를 연속하여 계산하고 저장한다. 아래 Fig 7.3을 보라

Backward pass #1: 이제 각 intermediate variables 에 대한 $l_i$의 derivatives를 계산한다. 여기서는 반대부터 계산된다.

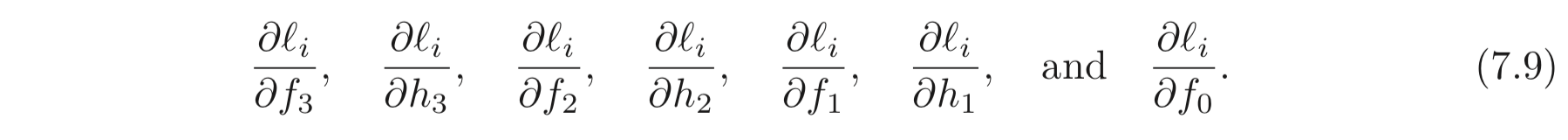
($l_i$) → ($f_3$) 방향의 backward pass 연산은 간단히 아래와 같이 계산된다.

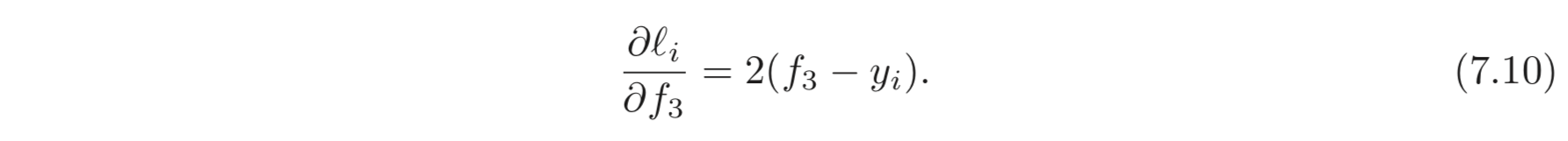
그리고 chain rule 에 따라 $(f_3) \rightarrow (h_3)$ 방향에 대한 backward pass도 아래와 같이 계산된다.

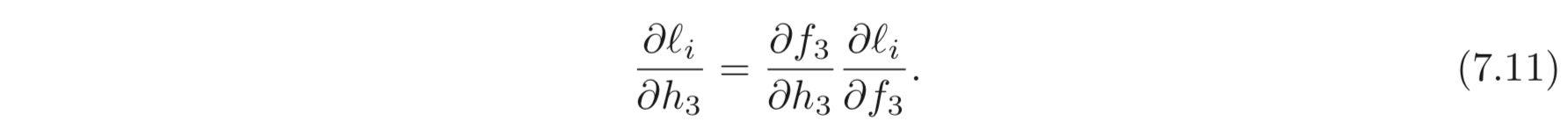
chain rule e.g.

좌항은 $l_i$가 $h_3$ 가 변했을 때 얼마나 변하는지에 대한 값이다. 우항은 이를 2개의 단계로 나누는데, (1) 먼저 $f_3$는 $h_3$가 변할 때 얼마나 변하는지를 먼저 구한다. (2) 다음으로, $l_i$가 $f_3$ 가 바뀔 때 얼마나 바뀌는지를 구하고 이들을 곱하여 최종적으로 $h_3$가 변할 때 $l_i$가 얼마나 변하는지를 계산한다.

중요한 점은 Eq. 7.11 을 계산할 때는 이미 앞선 $\frac{\partial l_i}{\partial f_3}$ 는 Eq. 7.10 에서 계산되었다는 점이다. (계산을 하지 않아도 된다는 것이다.) 위와 같은 방법을 반복하면 아래와 같이 최종적으로 거꾸로 모든 파라미터들에 대한 $l_i$의 derivatives를 계산할 수 있다.

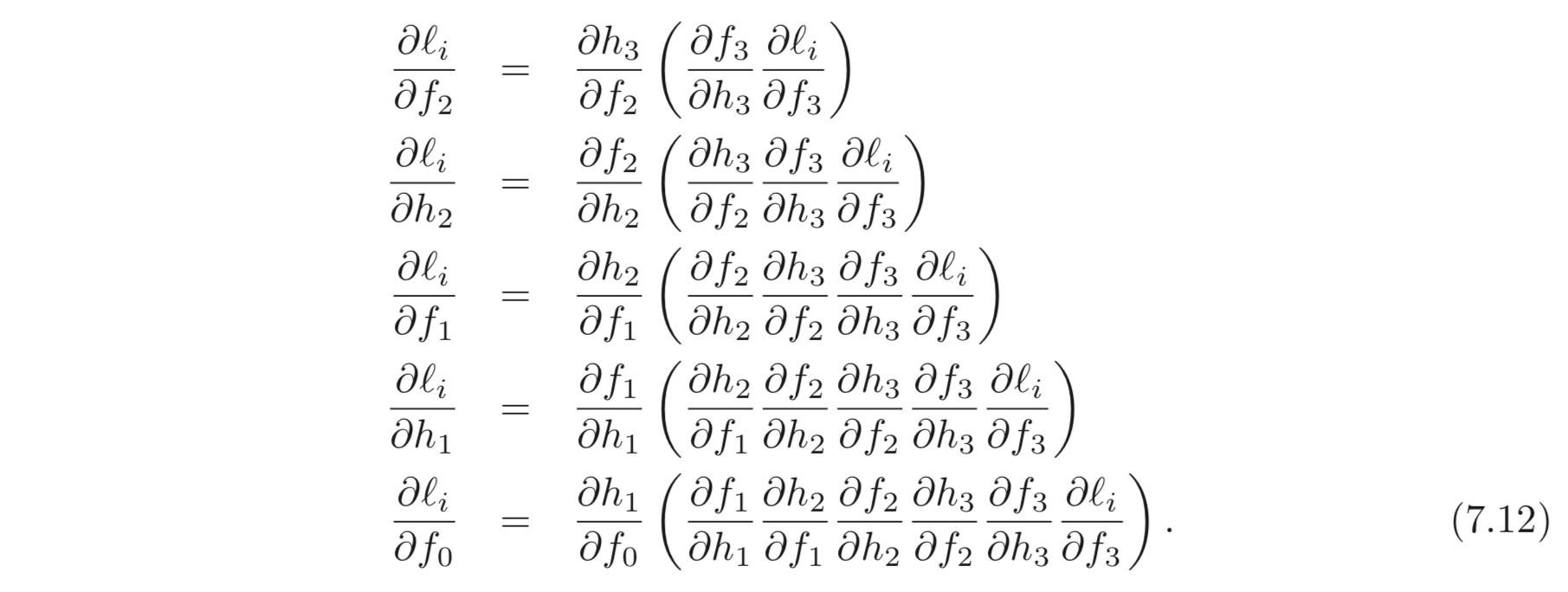
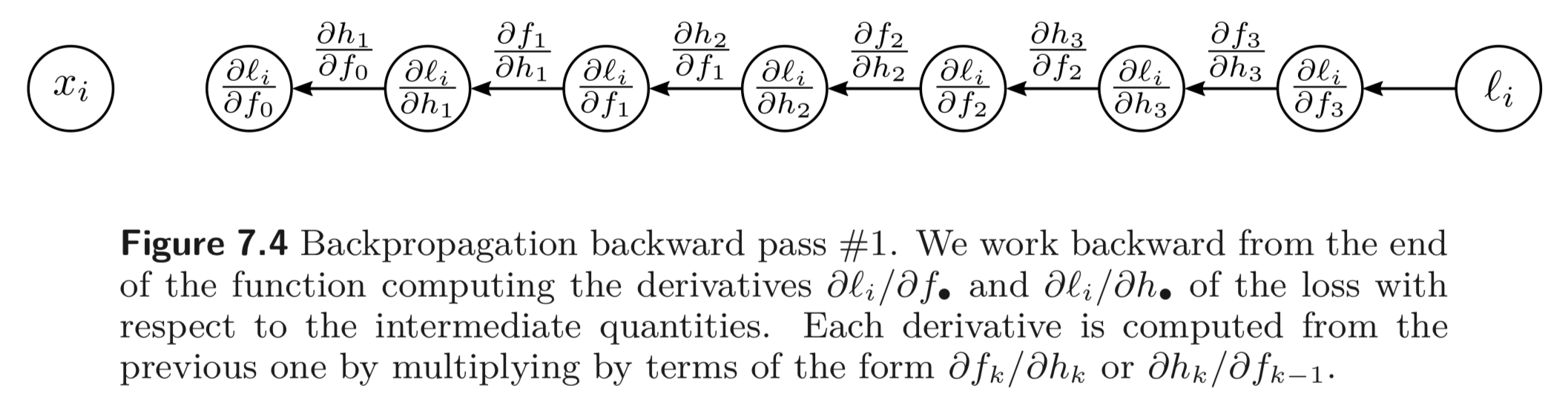
괄호가 쳐져있는 부분들은 앞에서 이미 계산이 된 부분들로 계산하지 않아도 된다.

Backward pass #2: 최종적으로 파라미터, $\beta_{\bullet}, \omega_{\bullet}$ 이 바뀜에 따라 loss, $l_i$가 바뀌는지 계산한다. 여기서도 다시 한 번 chain rule을 적용한다.

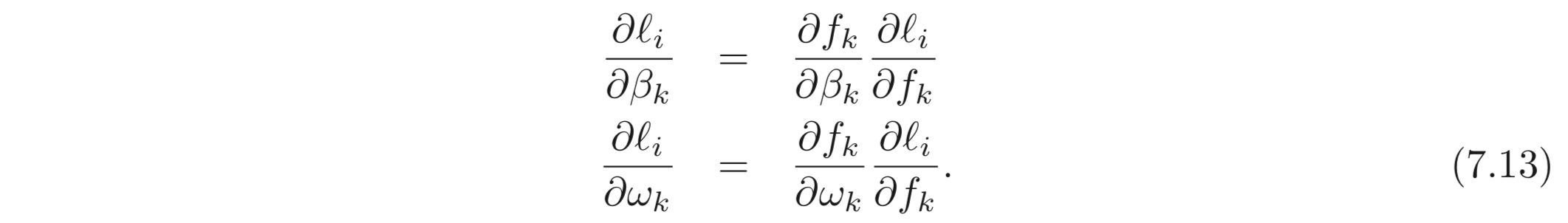
각 $k$ 에 대해서 우항에서 오른쪽에 있는 식들은 Eq. 7.12 에서 계산이 이미 된 식들이다. $f_k = \beta_k + \omega_k \cdot h_k$ 와 같이 계산되므로 우항의 왼쪽에 곱해지는 term들은 아래와 같이 계산된다.

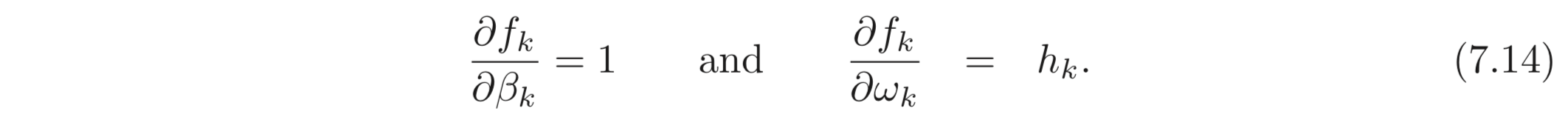
앞선 Fig 7.4를 확장하여 $\beta_{\bullet}, \omega_{\bullet}$ 에도 적용한 backward pass의 모습을 아래와 같다.

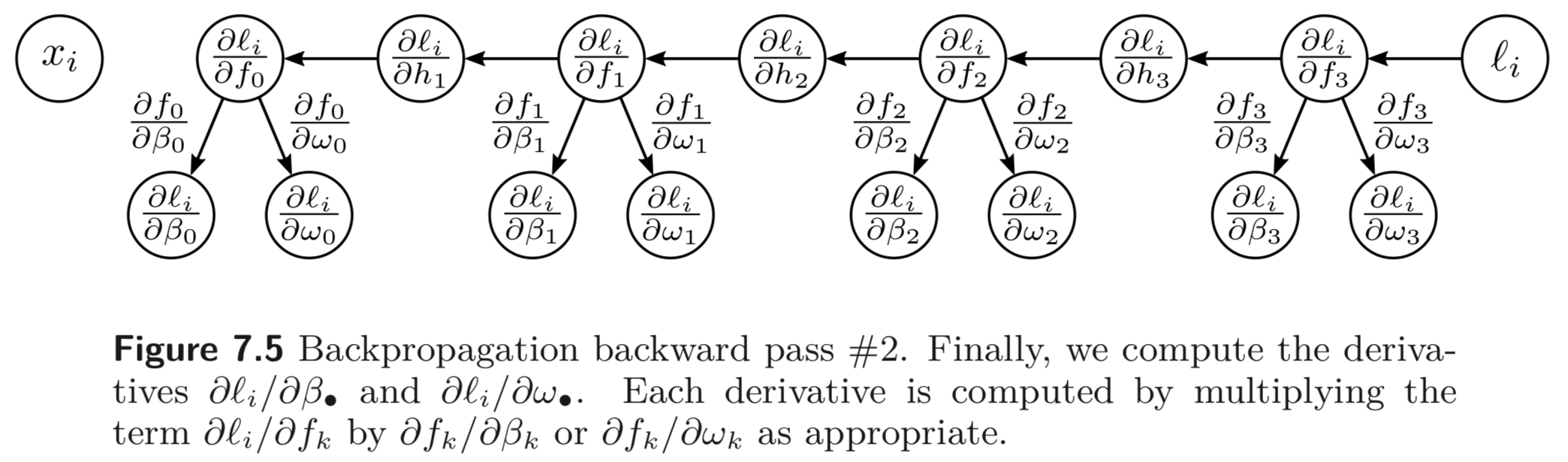
이러한 결과는 앞선 Observation 1 의 아주 작은 파라미터의 값의 변화라도 여러 레이어를 거치며 곱해지고 더해지며 결과 값에 큰 영향을 준다는 것과도 일맥상통한다. 입력단의 파라미터들의 derivatives들은 아래와 같다.

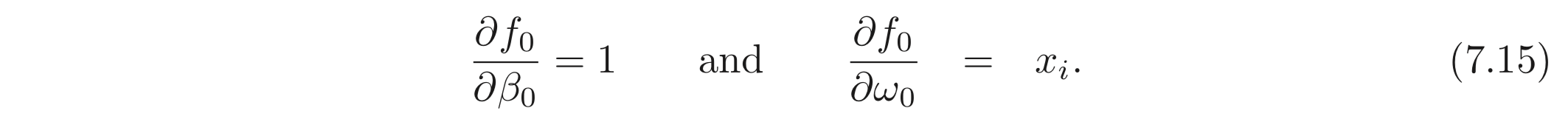
정리하자면, Backpropagation algorithm은 derivatives를 각각 구하는 (Eq 7.7) 방법보다 훨씬 간단하고 효율적이다.

7.4 Backpropagation Algorithm

다시 위 과정을 3-layers network 에 적용해보자 (Fig. 7.1). 앞에서 스칼라로 backprop 했던 통찰과 수학적인 방법은 동일하나 (중간 산출물) intermediate variables, $\bold{f}_k, \bold{h}_k$, bias, $\bold{\beta}_k$ 가 vector 란 점, 그리고 weights, $\bold{\Omega}_k$ 가 matrix 란 점이 차이점이다. 그리고 ReLU를 activation function으로 사용한다.

Forward Pass: 먼저 network를 sequential한 식들로 나열한다.

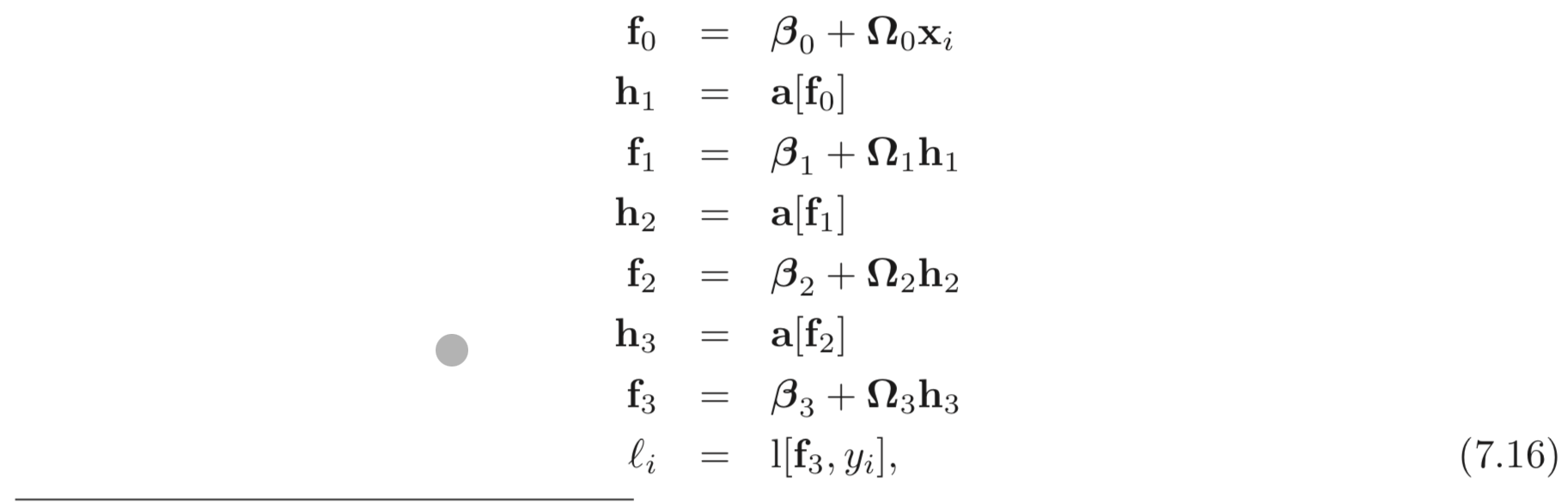
$l[\bold{f}_3, y_i]$ 는 MSE Loss or Binary Cross Entropy loss이다. forward pass 에서는 intermediates, $\bold{f}_k, \bold{h}_k, l$ 들의 값들을 모두 계산하고 결과를 저장한다.

Backward Pass #1:

먼저 $\bold{f}_2$에 대한 $l_i$ 의 derivatives 에 대한 식은 아래와 같다.

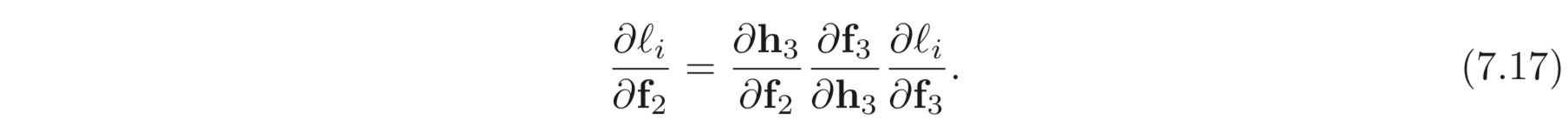
우항의 3개의 terms 들은 각각 $D_3\times D_3, D_3 \times D_f \text{ and } D_f\times 1$ 의 dimensions을 갖는다.
이와 같은 방법으로
$\bold{f}_1, \bold{f}_0$ 에 대해서도 derivative 를 구할 수 있다.

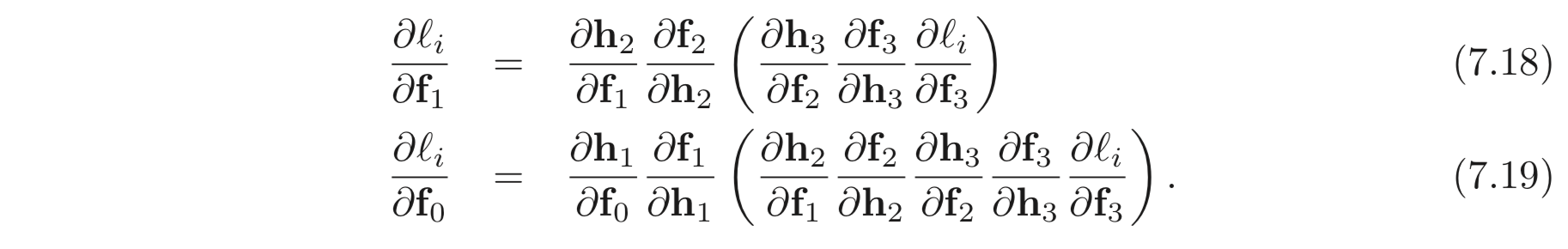
여기서 중요한 점은, 각 case 에 대하여 ( ) 안에 있는 부분들은 이미 앞서 계산이 되어 있다는 점이다. network 를 따라 거꾸로 계산한다면, 앞서 계산한 값들을 이용할 수 있다. 또한 각 terms은 그 자체로 심플하다. (직접 계산해보라.)

Backward Pass #2:

이제 $\bold{f}_k$ 에 대한 derivatives 를 계산할 수 있다. 지금부터는 weights와 bias 에 대하여 derivatives 를 어떻게 계산할지 알아보자.

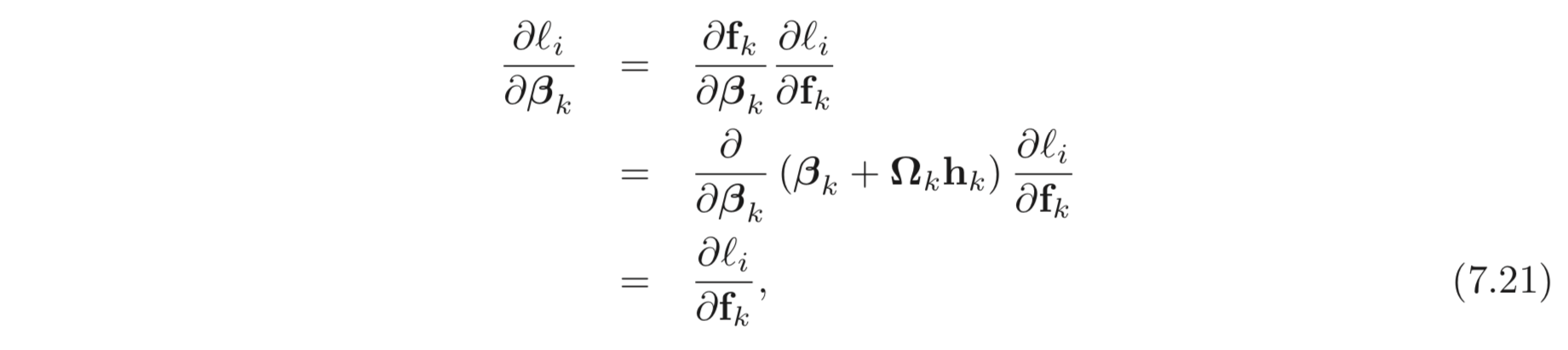
$\bold{\beta}$ 는 bias 기 때문에 미분하면 $1$ 이다. 따라서 앞선 derivatives, $\frac{\partial l_i}{\partial \bold{f}_k}$ 가 그대로 오는 것이다.

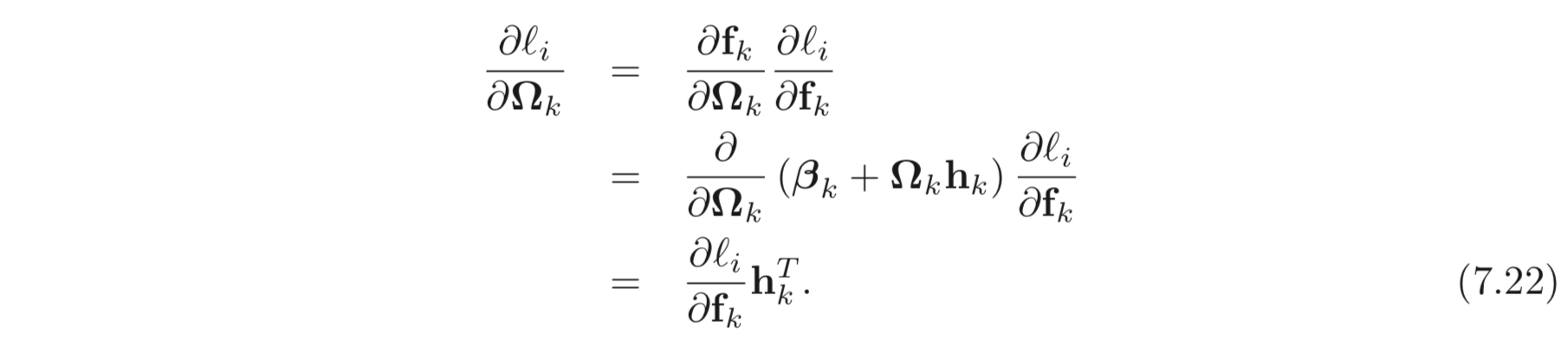
$\bold{\Omega}$ 는 미분하면 $\bold{h}_k^T$ 가 나오기 때문에 앞선 derivatives 와 곱하여 결과가 나온다.

7.4.1. Backpropagation Algorithm Summary

입력 $\bold{x}_i$ 를 받고 $K$개의 hidden layers 에 ReLU activation 을 갖는 Neural network, $\bold{f}[\bold{x}_i, \phi]$ 가 있고, loss는 $l_i = l[\bold{f}[\bold{x}_i, \phi], \bold{y}_i]$ 로 계산된다고 하자. Backpropagation 의 목표는 각 layer의 parameters, $\bold{\Omega}_k, \beta_k$ 의 derivatives를 계산하는 것이다.

Forward Pass:

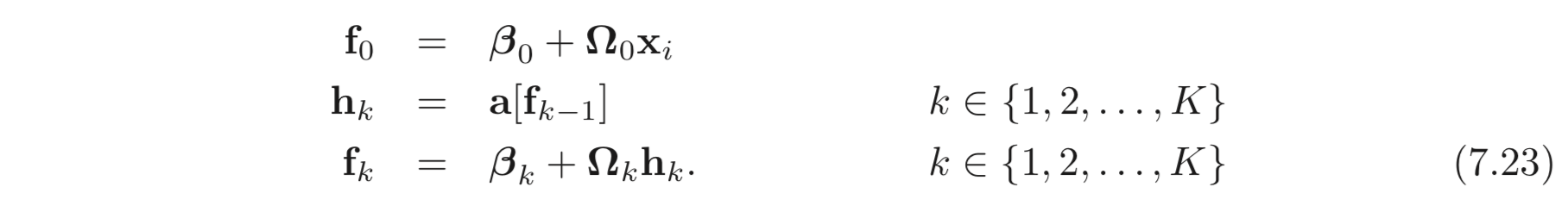
Backward Pass:

derivative $\partial l_i / \partial \bold{f}_K$ 부터 시작하여 거꾸로 아래와 같은 식으로 계산해나가면 모든 weights, biases 의 derivatives 를 계산할 수 있다.

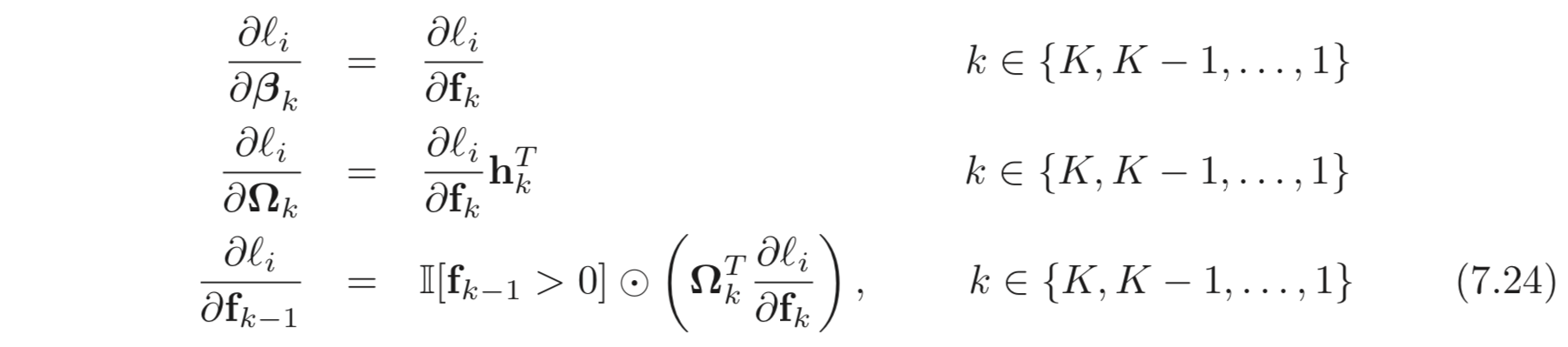
그리고 마지막으로 입력 layer의 derivatives 도 아래와 같이 계산할 수 있다.

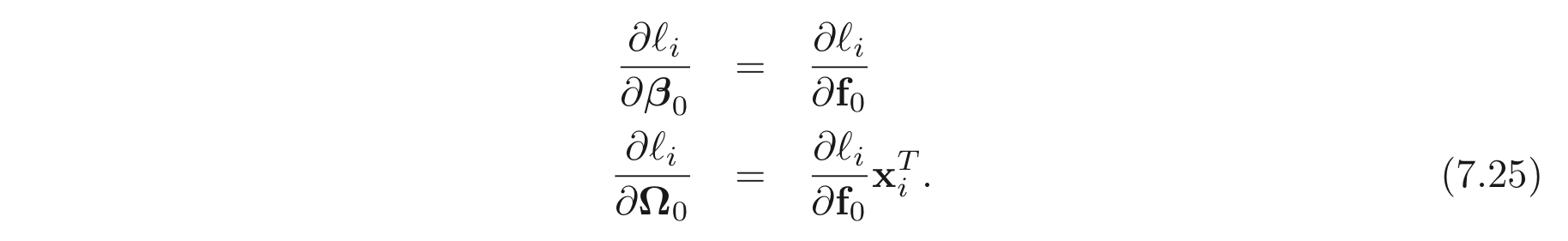
• Backpropagation algorithm 은 “계산적으로”는 정말 효율적이다. 하지만 “메모리적으로”는 전혀 효율적이지 못하다. 이러한 trade-off 로 모델의 학습은 VRAM의 크기에 따라 제한되기도 한다.

7.4.2. Algorithmic Differentiation

앞서 backprop 에 대해 열심히 공부했지만 이를 구현할 일은 없다. Pytorch, TF 와 같은 framework 들이 이를 훌륭히 지원해주기 때문이다. 이들을 Algorithmic Differentiation 이라고 한다.

7.5. Parameter Initialization

Backprop 알고리즘은 SGD, Adam 과 같은 optimization 알고리즘에 사용되는 derivatives를 계산한다. 본 챕터에서는 학습을 시작하기 전에 parameters 를 intialize 하는 법에 대하여 공부한다. 이게 왜 중요한지 보기 위하여 forward pass 에서 각 pre-activations 가 어떻게 계산되는지 보자.

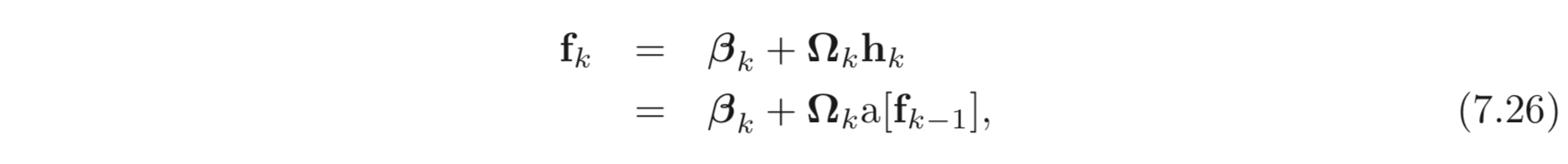
bias 는 모두 $0$, weights 는 모두 평균은 $0$, variance는 $\sigma^2$ 으로 초기화했다고 하자. 그리고 두 가지 상황을 가정한다.

1. $\sigma=10^{-5}$ 라고 하자. 그러면 그러면 하나의 layer를 통과할 때 모든 값들이 아주 작아질 것이고, bias도 $0$이기 때문에 ReLU를 통과하면서 절반은 $0$이 된다. 그리고 여러 layers를 통과하면서 계속해서 작아지게 된다.

2. $\sigma=10^5$ 라고 하면 1. 의 반대상황으로 매 layers 를 통과할 때마다 엄청나가 값이 커지게 된다.

위 두 가지 시나리오에서 pre-activations 이 너무 작거나 너무 크게 나타나질 수 있다는 사실을 알아보았다. 이들은 컴퓨터의 arithmatic precision 으로도 계산이 안될 것이다.

또한 backpropagation 으로 gradients 가 계산될텐데 여기서도 값이 엄청 작아지거나 엄청 커질 수 있다. 이러한 케이스를 각각 vanishing gradient problem 과 exploding gradient problem 이라고 한다.

Fig 7.7. Weight Initialization. 모든 레이어의 D_h 가 100인 경우에 a) 는 forward pass 의 각 layer 별 activations의 크기를, b) 는 backward pass 의 gradients 의 크기를 시각적으로 표현한 것이다. 각 레이어의 weights의 분포가 2/D_h = 0.02 일 때 forward pass, backward pass에서의 activations, gradients 가 안정적으로 유지 되는 것을 볼 수 있다.
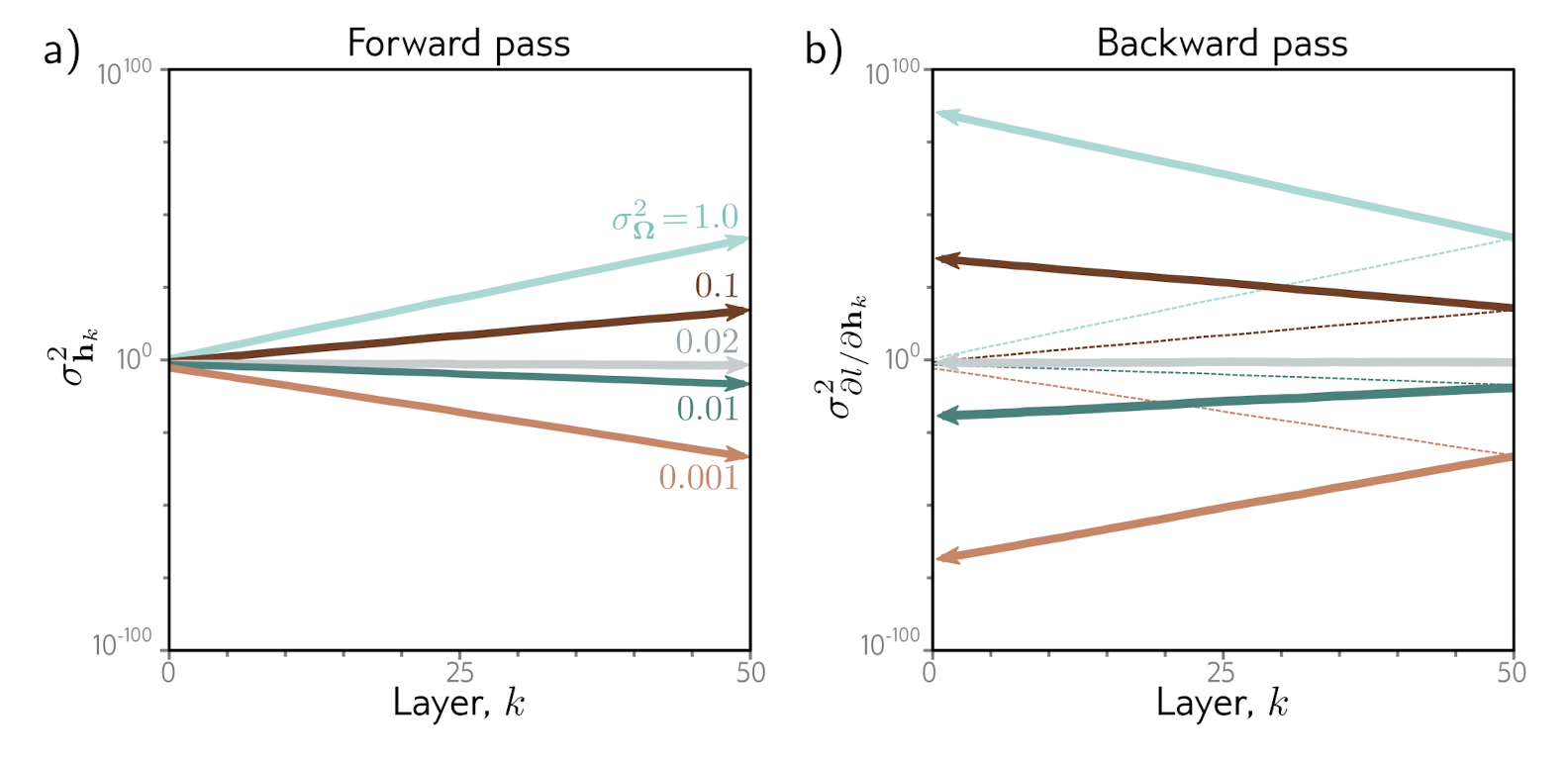
0.02 보다 작으면 vanishing gradient, 0.02 보다 크면 exploding gradient 문제가 발생할 수 있다.

7.5.1. He Initialization (ReLU 를 쓴다면 이 initialization 을 쓰세요)

각각 dimension, $D_h, D_{h'}$을 갖는 pre-activations, $\bold{f}, \bold{f'}$ 사이의 통계적인 분포에 대해 다루어보자.

$\bold{f}$의 $j$번째 element인 $f_j \sim N(0, \sigma_{\Omega}^2)$ 이며, bias, $\beta$는 $0$이며, weight, $\Omega$ 의 한 element인 ${\Omega}_{ij} \sim N(0, \sigma_{\Omega}^2)$ 이다.

우리는 여기서 $\bold{f'}$ 가 $\bold{f}$ 의 분포를 따르기 원한다 (분포가 다르기 때문에 vanishing(or exploding) gradient 문제가 생기기 때문). $\bold{f'}$ 의 통계적 특성을 구하기 위해 $\bold{f'}$ 의 한 element 인 $f'_i$ 를 먼저 구한다.

$$h_j = \text{ReLU}[f_j] \\ f'_i = \beta_i + \Omega_{ij}h_j$$

$f'_i$ 의 Expectation 은 아래와 같이 계산할 수 있다.

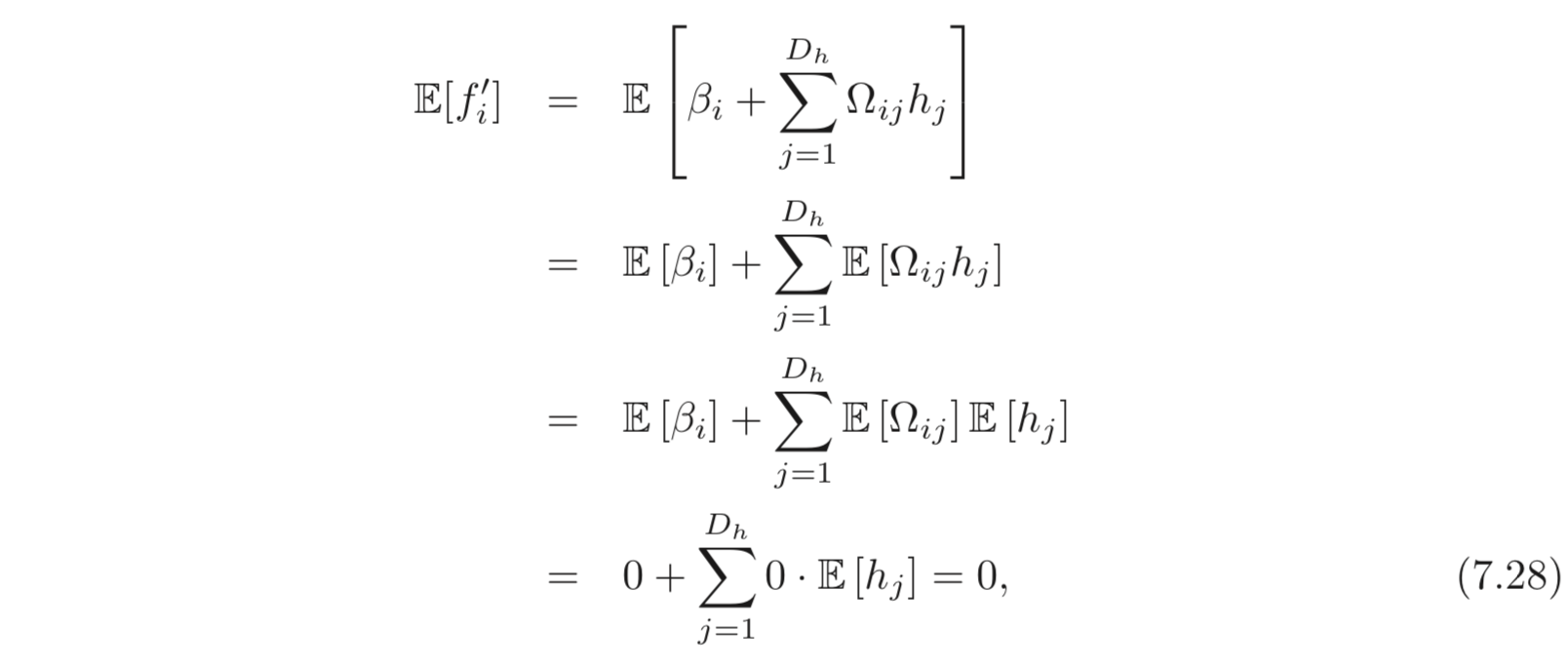
$f'_i$ 의 variance 는 아래와 같이 계산할 수 있다.

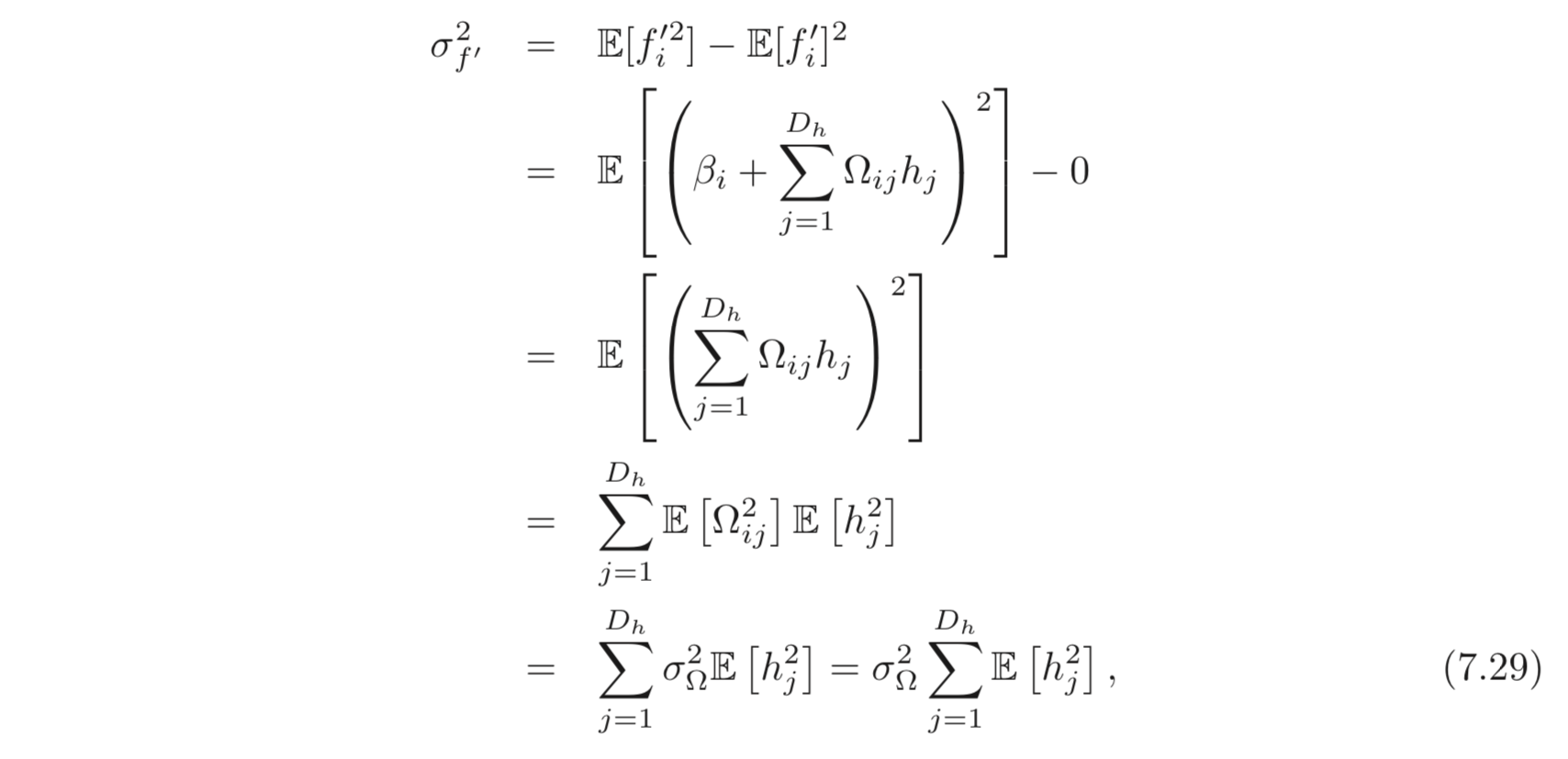
여기서 $\Bbb{E}[f_j^2] = \Bbb{E}[f_j^2] - 0 = \Bbb{E}[f_j^2] - \Bbb{E}[f_j]^2 = \Bbb{V}[f_j]$ 으로 표현할 수 있고, 평균이 $0$ 이므로 ReLU activation 을 통과하며 절반만 남기 때문에 이를 아래와 같이 다시 나타낼 수 있다.

$$\sigma_{f'}^2 = \sigma_{\Omega}^2 \frac{1}{2} \displaystyle\sum_{j=1}^{D_h}\Bbb{E}[f_j^2] = \sigma_{\Omega}^2 \frac{1}{2} \displaystyle\sum_{j=1}^{D_h}\Bbb{V}[f_j] = \sigma_{\Omega}^2 \frac{1}{2}D_h \sigma_f^2$$

따라서 $\sigma_{f'}^2 = \sigma_{f}^2$ 이 되려면, 아래 조건이 성립해야한다.

$$\sigma_{\Omega}^2 = \frac{2}{D_h}$$

이것이 바로 He Initialization 이다.

7.5.3. Initialization for both forward and backward pass

weight matrix가 정방행렬이라면, 앞선 정의로도 문제가 안되지만, 각 layer의 크기가 다르기 때문에 이는 문제가 된다. 따라서 forward, backward pass 모두를 고려한 He Initialization은 아래와 같다.

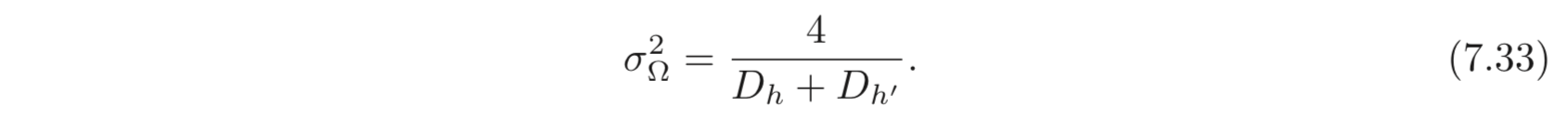
Uploaded by N2T