[Deep Learning] Fitting Models

본 포스팅은 Simon J.D. Prince 의 Deep Learning 교재를 스터디하며 정리한 글임을 밝힙니다.

https://udlbook.github.io/udlbook/

Take Home

1. 모델을 학습하는 것은 파라미터, $\phi$ 에 대응하는 loss function, $L[\phi]$ 를 최소화하는 것으로 생각할 수 있다. Gradient Descent 는 현재 파라미터에서 계산되는 loss의 (해당 지점에서의 uphill) gradient를 계산하고 이의 반대방향인 downhill (gradient에 $\times -1$ 을 곱하면 됨.) 방향으로 파라미터를 업데이트 한다.

2. non-linear function 에 대한 loss는 non-convex일 확률이 아주아주 높다. 따라서 local-minima나 saddle points를 포함할 수 있다. Stochastic Gradient Descent (SGD) 는 이러한 문제를 어느 정도 해결할 수 있다.

3. SGD는 학습 데이터에서 중복을 허용하지 않게 몇몇 examples 를 샘플링한다. 이들을 batch 혹은 minibatch 라고 한다. 이 batch에 대하여 loss와 gradient를 계산한다. 이러한 접근은 gradient에 noise를 더한다고 볼 수 있고 이러한 과정에서 앞선 local minima, saddle points를 피하도록 하며 학습 데이터를 더 잘 일반화한다.

4. 마지막으로 이러한 SGD 알고리즘에 momentum term 을 추가하는 것이 학습을 효과적으로 도울 수 있음을 보았고, Vanilla momentum, Nesterov Accelerated momentum, Adaptive Momentum Estimate (Adam) 까지 살펴보았다.

---

들어가기 앞서

Chapter 3, 4 에서는 SNN, DNN에 대하여 공부하였다. 이러한 모델들의 파라미터들이 어떤 함수를 나타내는 여러 개의 piecewise line function들로 표현된다. Chapter 5에서는 loss 에 대하여 공부하였다. 이는 학습 데이터에 대하여 ground truth (GT = 정답) 과 모델의 prediction 간의 mismatch 를 나타내는 하나의 스칼라 값이다.

loss는 모델의 파라미터에 따라 결정되는 값이고, 본 챕터에서는 loss가 최소값을 갖는 파라미터를 “어떻게 찾는지” 에 대하여 공부를 한다. 이러한 방법을 learning, training 혹은 fitting 이라고 한다.

먼저 파라미터의 값을 초기화하고 크게 다음과 같은 두 개의 스텝을 따른다.

1. 파라미터에 대한 loss의 derivative(==미분) (gradient) 를 구한다.

2. 앞서 구한 gradient 에 대하여 loss가 작아지도록 파라미터를 조정한다.

여러 반복 뒤에 loss function의 전반적인 minimum에 도달하기를 기도한다. (fitting은 샤머니즘의 영역..)

6.1 Gradient Descent

optimization algorithm 의 최종 목표는 바로 loss를 최소화하는 파라미터, $\hat{\phi}$를 찾는 것이다.

$$\hat{\phi} = \displaystyle\argmin_{\phi}\bigg[L[\phi]\bigg], \\\text{Eq. 6.1}$$

다양한 optimization algorithm이 존재하지만 보통 neural network 를 학습하는 일반적인 방법은 먼저 파라미터의 값을 휴리스틱 (휴리스틱은 말이 좋아 휴리스틱이지 그냥 감으로 때려박는 것.) (initialization 에 대해서는 후술할 예정) 하게 initialization 하고 loss가 줄어드는 일련의 방법을 반복하여 (iterative) optimization 하는 것이다.

이러한 알고리즘 중에서 가장 심플한 방법은 gradient descent 이다. 이는 먼저 파라미터, $\phi = [\phi_0, \phi_1, ..., \phi_N]^T$ 로 초기화 하고 아래 두 step을 반복한다.

Step 1. $\phi$에 대한 loss의 gradient 를 계산한다.

$$\frac{\partial L }{\partial \phi} = \begin{bmatrix} \frac{\partial L}{\partial \phi_0} \\ \frac{\partial L}{\partial \phi_1} \\ \vdots\\ \frac{\partial L}{\partial \phi_N} \\ \end{bmatrix}, \text{ Eq. 6.2}$$

Step 2. rule에 따라 $\phi$를 업데이트한다.

$$\phi \leftarrow \phi - \alpha \cdot \frac{\partial L}{\partial \phi}, \text{ Eq. 6.3}$$

$\alpha$는 업데이트의 크기를 결정하는 scalar 값이다.

Step 1. 에서는 계산한 loss 값을 현재의 $\phi$에 대하여 미분하여 gradient를 구한다. 이 gradient는 loss function의 uphill 의 방향과 크기를 결정한다. Step 2. 에서는 살짝 $\alpha$ 만큼만 downhill 방향으로 내려간다 (그래서 $-$ 가 곱해진 것). 이러한 $\alpha$는 고정될 수도 있고, (이러한 경우에 $\alpha$는 learning rate 이라고 불린다.) loss를 가장 크게 줄일 수 있는 $\alpha$를 찾는 line search 를 할 수도 있다.

loss function의 최소값에서는 loss function의 surface가 평평할 것이기다 (기울기가 $0$). 학습이 다 되면 파라미터가 더 이상 크게 변하지 않게 될 것이다. 실제로는 gradient의 크기를 모니터링 하여 너무 작아지면 학습을 중단한다 (early stopping).

6.1.1 Linear Regression Example

SNN의 예제를 가져와보자. scalar $x, y$ 를 mapping 하는 모델, $y = f[x, \phi] = \phi_0 + \phi_1 x$ 이 있다고 하자.

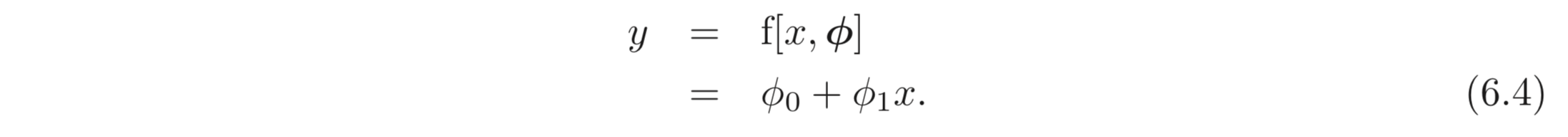
$I$ 개의 샘플을 갖는 학습 데이터, $\{ x_i, y_i \}$ 가 주어졌을 때, MES Loss 를 선택하여 이들을 fitting 한다고 하자.

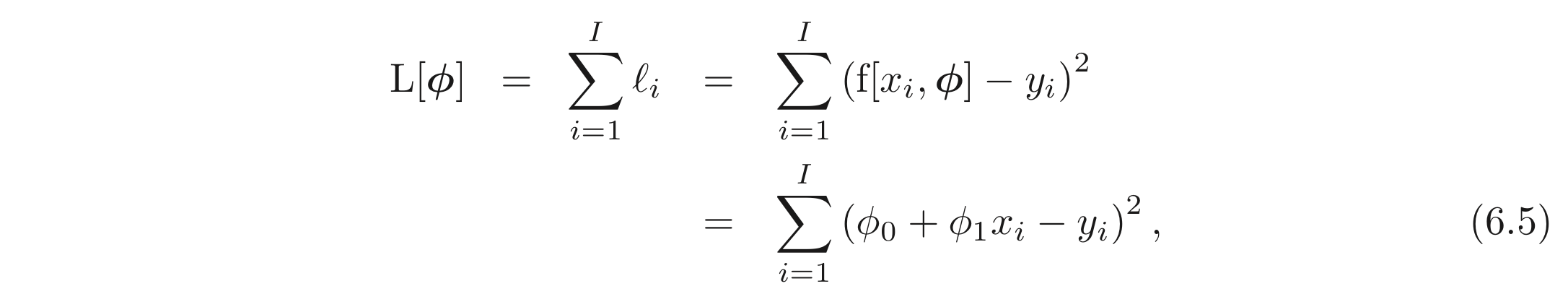
$\mathscr{l}_i = (\phi_0 + \phi_1x_i-y_i)^2$ 은 $i^{th}$ example 의 loss 이며, 최종 loss에 기여한다. $L = \displaystyle\sum_{i=1}^{I}l_i$ 이므로 아래 식이 성립한다.

$$\frac{\partial L}{\partial \phi} = \frac{\partial}{\partial \phi}\displaystyle\sum_{i=1}^{I}l_i = \displaystyle\sum_{i=1}^{I}\frac{\partial l_i}{\partial \phi}, \text{ Eq. 6.6}$$

$i^{th}$ 의 $\phi$ 에 대한 $l_i$ 의 gradient 는 아래와 같이 계산될 수 있다.

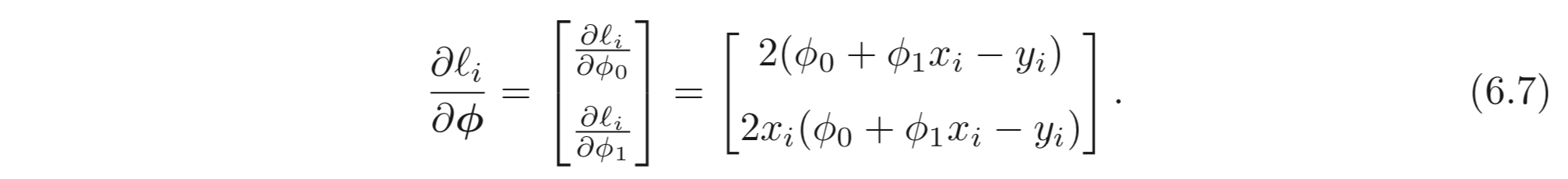
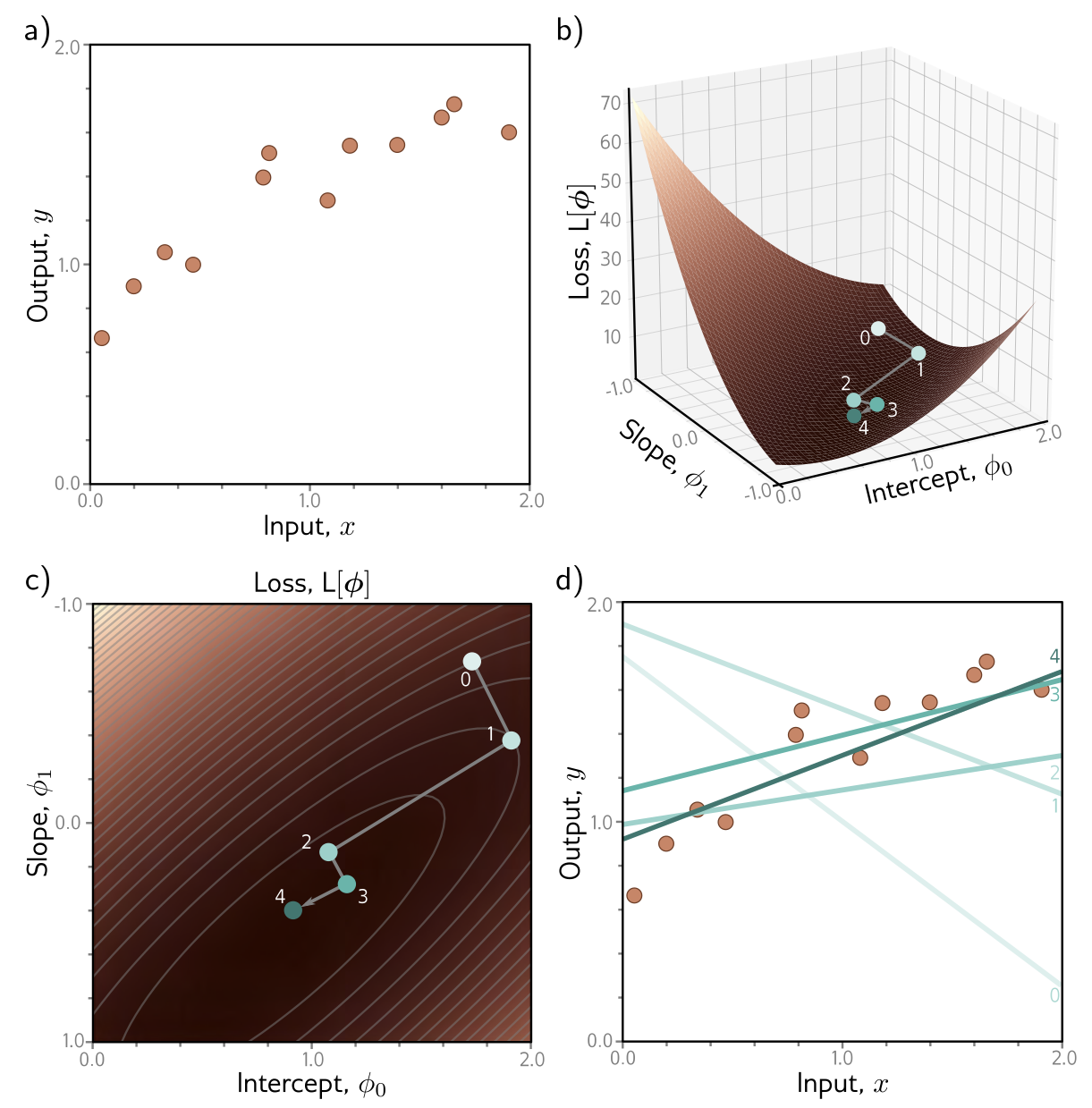
아래 Fig. 6.1 은 Eq. 6.6, 6.7 에 따라 derivative 를 구하고, Eq. 6.3 에 따라 파라미터를 업데이트하는 과정을 반복함에 따라 어떻게 학습이 진행되는지를 나타낸다. 아래 예제에서는 각 스텝에서 loss가 최소화 되도록 하는 $\alpha$를 찾기 위해 line search 를 수행한다.

Fig. 6.1: Gradient descent for linear regression. a) 학습 데이터, b, c) loss 함수에 따 gradient descent 를 수행한 과정들. 0 에서 출발하여 1, 2, 3, 4 에 도달하는 과정을 나타낸다. b) 에서 괄목할만한 것은 “line search” 를 했다는 점이다. learning rate을 고정하지 않고 downhill 방향의 모든 loss를 구하여 가장 낮은 곳을 찾는다. 이러한 과정을 반복하여 4까지 이동한다. d) 는 loss 에 따라 결정된 파라미터로 그려진 linear function 을 나타낸 것이다. loss가 작을 수록 학습 데이터를 잘 나타내는 선을 그린다.

6.1.2 Gabor Model Example

앞선 예제에와 같은 linear regression 문제는 하나의 잘 정의된 global minimum을 갖는다. 더 있어 보이게는 이들을 convex 라고 한다

💡

convex 위의 임의의 두 점을 이은 chord (현) 은 함수와 교차하지 않는다.

Convexity 라는 뜻은 파라미터가 어느 지점으로 initialization 되더라도 downhill로 열심히 내려간다면 global minimum에 도달하는 것을 암시하며, 학습에 항상 성공한다.

하지만 대부분의 SNN, DNN을 포함한 non-linear 모델들은 보통 non-convex 이다. 모델의 loss 함수를 visualization 하는 것은 쉽지 않다. non-convex 함수의 loss function의 특징에 대한 통찰력을 얻기 위해 먼저 간단한 non-linear 함수를 예시로 알아보자.:

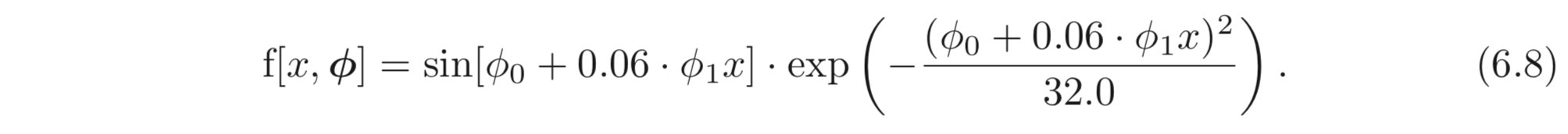
위와 같이 scalar $x, y$ 로의 mapping 을 나타내는 Gabor model 은 sinusoidal 함수를 포함하고 $e^{\R^-}$ 에 곱해져있다. $sin$ 함수는 oscillation 하며, $e^{\R^-}$는 센터로부터 멀어지면 값이 작아지도록 한다. 이는 두 개의 파라미터, $\phi=[\phi_0, \phi_1]^T$ 를 가지며, $\phi_0 \in \R, \phi_1 \in \R^+$ 이고 각각 mean과 variation 을 나타낸다.

Fig. 6.2: Gabor model 예시.

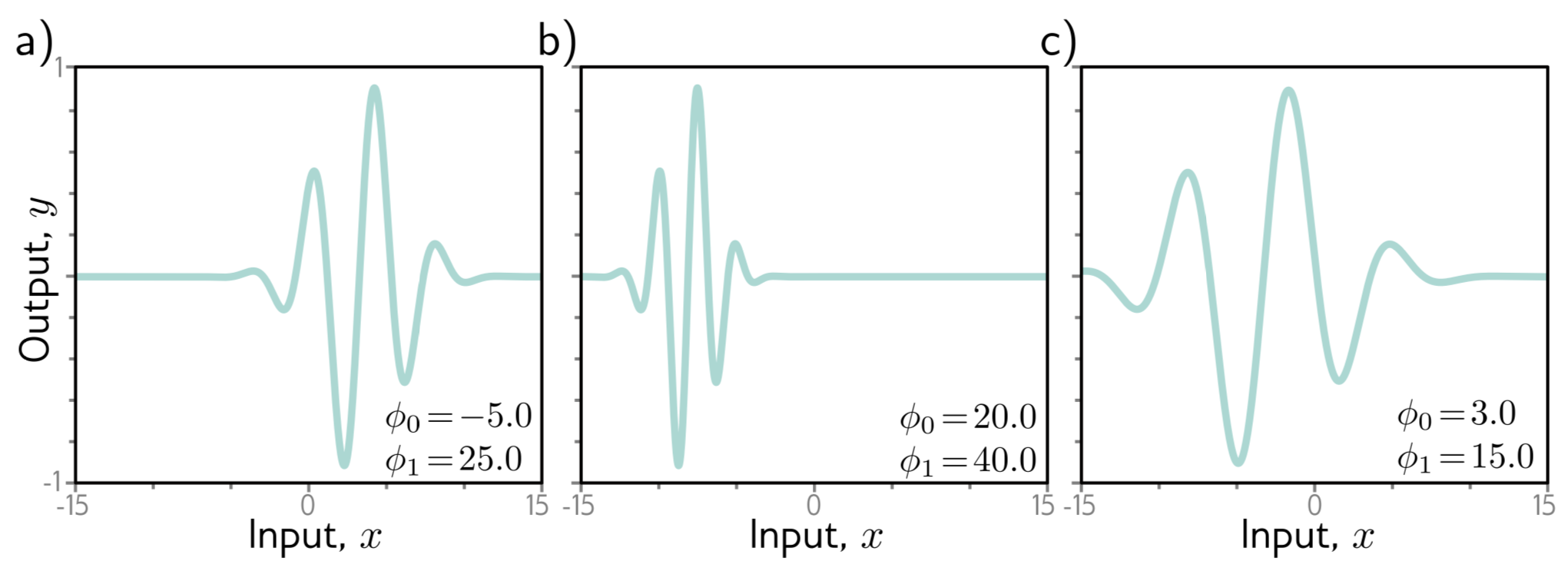
$I$ 개의 학습 데이터, $\{x_i, y_i\}$ (Fig. 6.3) 에 MES Loss를 적용한 것을 고려해보자.

Fig. 6.3: Gabor model 예제에 사용되는 학습 데이터 예시. mean=0.0, var=16.6 에 해당하는 Gabor model에 noise를 더한 28개의 examples

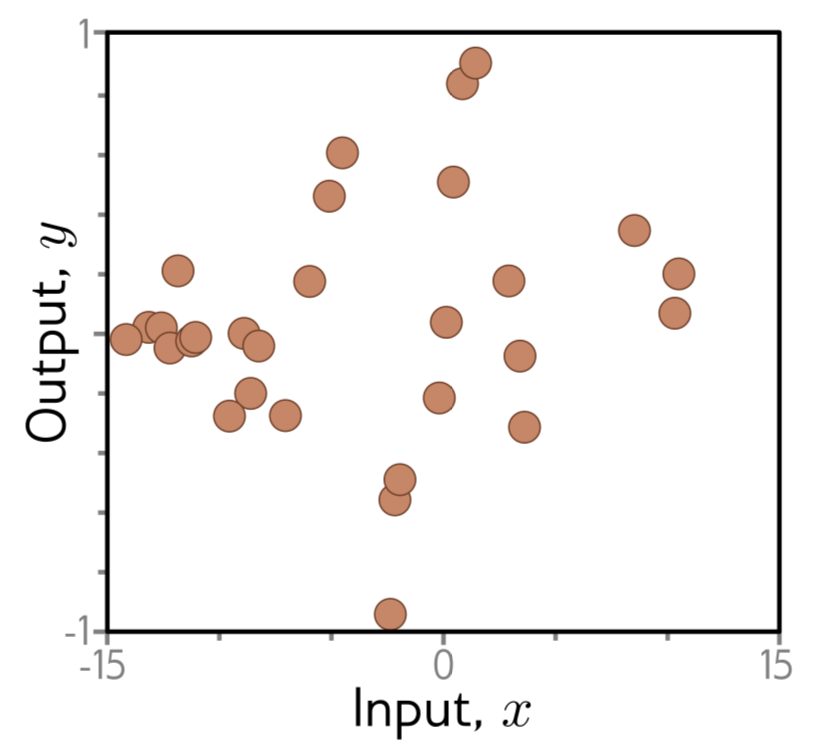
Loss function은 아래와 같이 계산될 수 있다.

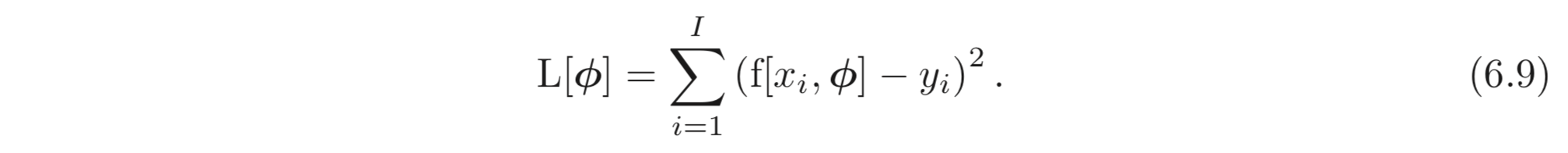
6.1.3 Local Minima and Saddle Points

Fig. 6.4 는 위 학습 데이터에와 Gabor model 에 대한 loss function 을 나타낸다.

Fig. 6.4: Loss function for Gabor model. a) loss function이 non-convex임을 보임. gray point가 global minima, cyan points가 local minima 이다. 십자 표시는 gradient 가 0이 되는 saddle point를 나타낸다. b-f) 각 minima 에 대응되는 뉴럴넷의 모델을 나타낸다. c) 가 global minima이다. (가장 loss가 작음.)

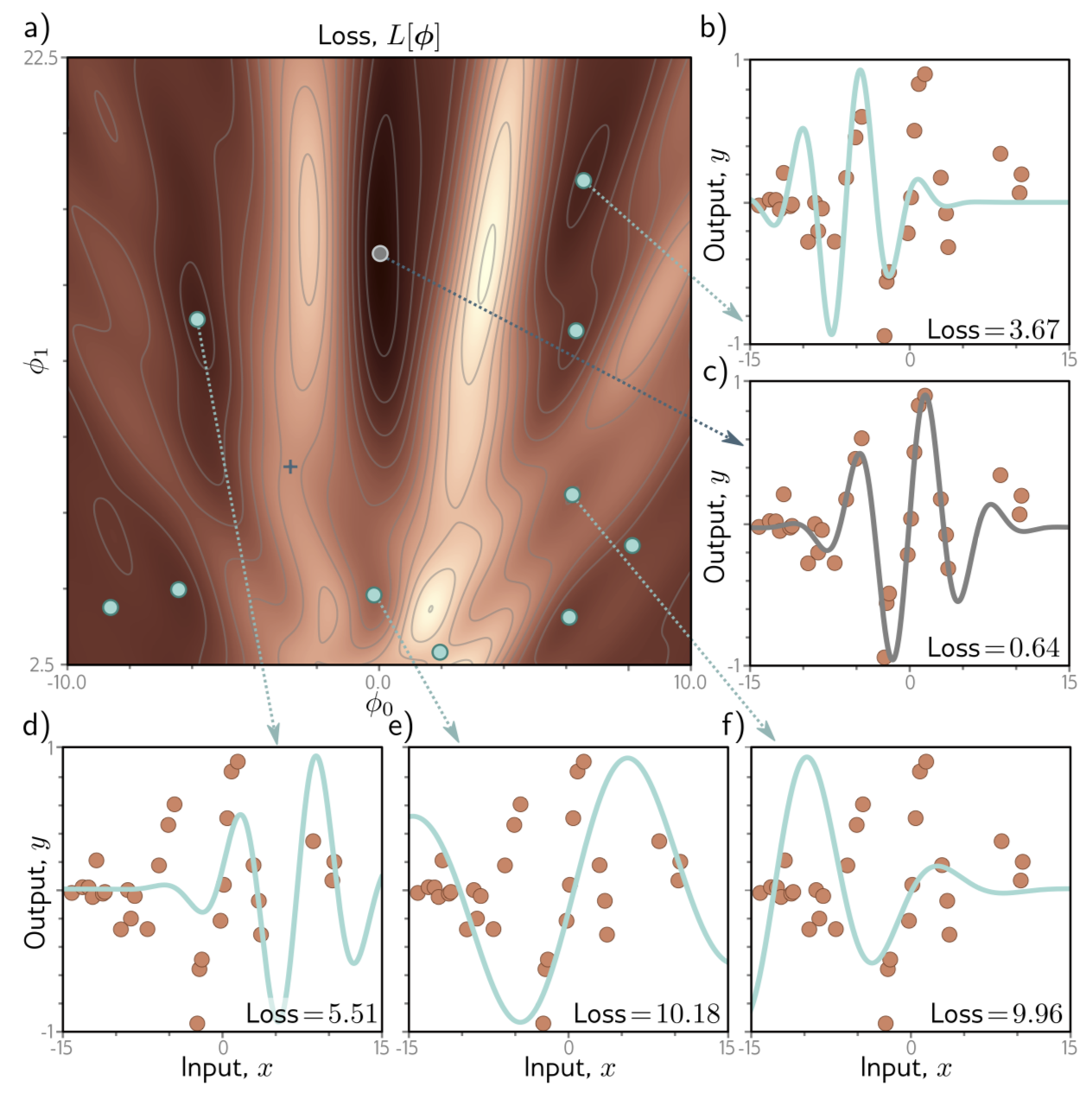
Fig. 6.4 의 a) 에는 다양한 minima (어느 방향으로 가던 loss가 증가함.), 가 존재한다. 이런 minima 들 중 loss가 최소가 되는 포인트가 global minimum(gray) 이고 그렇지 않은 다른 minima들을 local minima(cyan) 라고 한다.

학습을 할 때, 임의의 위치에서 GD를 사용하여 downhill을 내려가게 된다면 global minimum을 찾아 최고의 파라미터를 찾을거라고 보장할 수 없다. 오히려 local minima에 도달할 확률이 global minima 에 도달할 확률과 못해도 갖거나 훨씬 크다. 그리고 minima를 찾아도 찾은 minima가 global minima라는 보장도 없다.

그리고 loss function은 saddle points를 갖는다. ($x^3$ 함수에서 $x=0$ 에서의 기울기를 생각해보라 (뚫접)) saddle point는 기울기는 0이지만 어느 방향으로 증가하거나 감소하고 있는 포인트를 의미한다. 학습 과정 중 다행히 saddle points를 피하면 다행이지만, 만약 saddle points 주변에 떨어진다면 gradient가 작아 학습이 거의 이루어지지 않는 것처럼 보인다. 이러한 경우 학습이 완료된 것인지 local minima에 떨어진 것인지 알 수 없다.

6.2 Stochastic Gradient Descent

위와 같은 Gabor model 예제에서 보다시피 random point ($\phi$ 를 random 으로 initialization) 에서 시작하여 GD로 global minimum에 도달하는 것을 보장할 수 없다. 이빨이 없으면 잇몸으로 씹는 심정으로 다음과 같은 두 개의 방법을 생각해볼 수 있다.

1. exhaustively searching. (SAT slover와 같은 non-iterative method를 사용하여 구함.)

2. starting points 를 바꿔가며 여러번 GD를 수행해서 가장 loss가 낮은 파라미터를 사용한다.

하지만 통상의 뉴럴 모델들은 수억개의 파라미터도 갖기 때문에 시간, 비용 상의 이유로 위와 같은 두 가지의 방법은 현실적이지 못하다.

정리하면, high-dimensional loss function의 global minimim을 gradient descent 알고리즘으로 찾는 것은 challenging 하다.

먼저 이러한 방법으로 찾는 minima가 global minima 라는 보장이 없으며, initial points 에 크게 의존적이라는 것이 문제가 된다. (순전히 좋은 initial point에서 시작해야 좋은 학습이 되기 때문임.)

이러한 문제를 어느 정도 해결하기 위해 Stochastic Gradient Descent (SGD) method가 제안되었다. SGD는 매 학습마다 gradient 에 noise를 더하는 것으로 볼 수 있다. SGD에서 계산된 gradient의 평균은 full-batch SGD, 즉 GD의 gradient와 같다. 하지만 매 step마다 일부분의 데이터로 gradient가 계산되므로 모든 데이터로 계산된 gradient의 방향과 약간 다른 방향 (noise가 더해진 방향이라고 볼 수 있음.) 으로 내려간다고 볼 수 있다.

이러한 SGD의 “noisy” 한 특성 때문에 모든 loss function에서 downhill로 내려가는 것이 아닌 uphill로 올라갈 수도 있게 된다. 즉, local minima에서 탈출할 수 있는 가능성이 생긴다.

6.2.1 Batches and epochs

앞선 SGD의 예처럼, 학습에 randomness를 주는 것은 간단하다. 각 iteration 마다 알고리즘은 전체 데이터셋의 일부 (subset) 를 랜덤하게 샘플링하고 샘플링한 데이터를 가지고 gradient를 계산하는 것이다. 이러한 일부 (subset) 을 보통 batch 혹은 minibatch 라고 부른다. batch로 파라미터를 업데이트 하는 것은 아래와 같다.

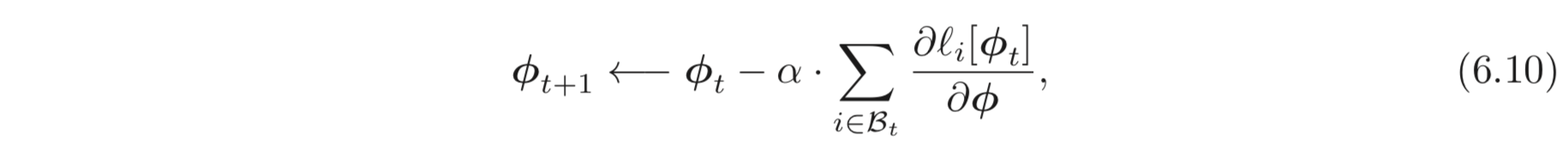
$\mathcal{B}_t$ 는 현재 batch의 input/output pairs의 indices를 포함한다. $l_i$ 는 $i^{th}$ iteration의 loss이다.

batch 는 보통 중복을 허용하지 않고 (without replacement) 데이터셋으로부터 샘플링한다. 이러한 과정을 알고리즘은 모든 데이터를 뽑을 때까지 수행하고, 모두 뽑은 그 순간이 다시 처음부터 다시 반복하는 순간이 된다. 이와 같은 과정을 모든 데이터셋에 대해서 한 번 수행하는 것을 epoch 이라고 한다. batch의 크기는 하나의 example 일 수도 있고, 모든 학습 데이터를 모두 포함할 수도 있는데 이러한 경우는 full-batch gradient descent 라고 하며 GD와 동일하다.

SGD의 다른 해석으로는 각 iteration 마다 샘플링된 batch로 구해진 서로 다른 loss로 gradient를 계산한다는 것이 있다. 아래 Fig 6.6 예시를 보자.

Fig 6.6: alternative view of SGD for Gabor model with a batch size of 3. a) 모든 학습 데이터로 계산된 loss function. b) 3의 크기를 갖는 batch의 loss function. 샘플링된 batch로 계산된 loss의 gradient를 따라 파라미터를 update함. “- - -” 그려진 그래프에서 “——” 로 그려진 그래프로 주어진 샘플에 대해서 더 잘 fitting 된 쪽으로 파라미터가 업데이트 되었다. c) 다른 배치의 예시. d) 샘플링된 batch 에 대해서는 downhill로 내려가지만 global loss에 대해서는 uphill로 올라간다.

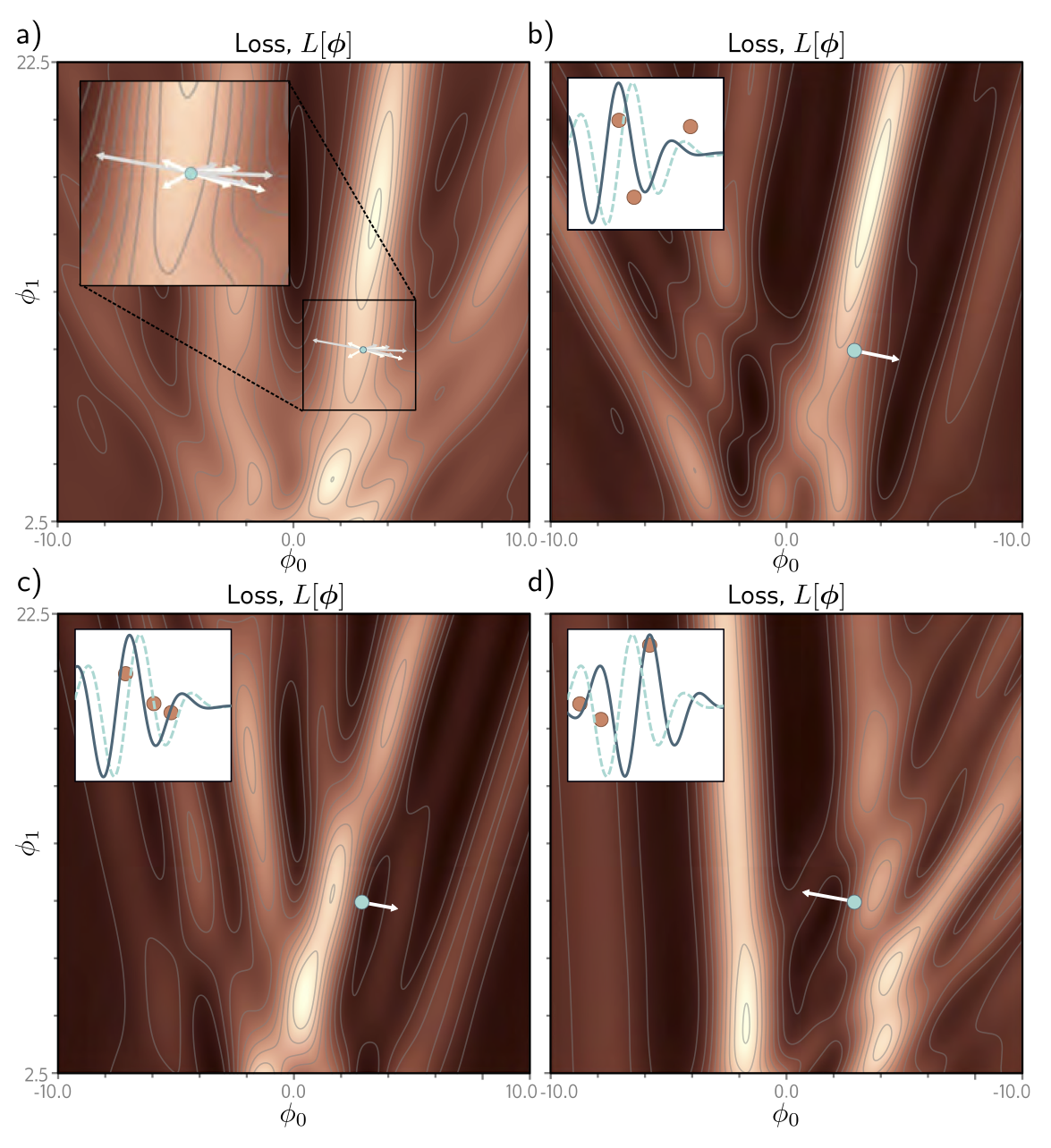
위와 같이 SGD는 GD보다 variability를 가져도 loss와 gradient의 평균은 결국 GD의 loss, gradient와 같다는 한계가 있다.

6.2.2 Properties of Stochastic Gradient Descent

SGD는 아래와 같은 좋은 특징들이 있다.

1. loss function을 내려가는 (= downhill을 내려가는) trajectory에 noise가 끼어도 매 iteration 마다 여전히 모델을 데이터의 subset에 대하여 fitting 한다.

2. 각 batch를 “중복 없이” 샘플링 하기 때문에 모든 examples가 gradient에 똑같이 영향을 준다.

3. 모든 데이터셋에 대하여 gradient를 구하는 것보다 연산량이 적다.

4. local minima에서 탈출할 수 있는 가능성이 있다.

5. saddle points에 걸릴 확률이 낮아진다.

6. 학습 데이터에 대하여 더 잘 “일반화” (새로운 데이터에 대하여 robust하다.) 한다.

6.3 Momentum

SGD의 성능을 개선시키기 위해 주로 사용되는 방법은 momentum term 을 추가하는 것이다. 현재 batch로 계산된 gradient와 이전 스텝에서 계산된 방향을 weighted combination 하여 파라미터를 업데이트한다.

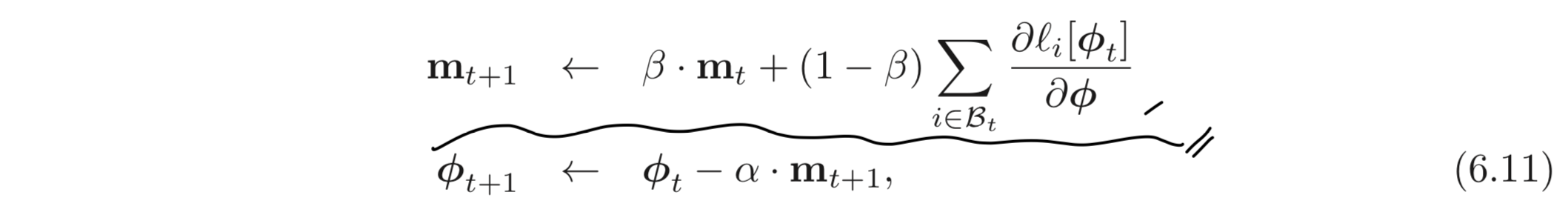
$\bold{m}_t$ 는 time step, $t$ 에서의 momentum이며, $\beta \in [0, 1)$ 은 시간에 따라 gradient가 smooth 해지도록 조정하는 값이다.

위와 같은 momentum을 계산하는 recursive fomulation은 이전에 계산된 모든 gradient를 모두 weighted sum 한 것으로 여길 수 있으며, 더 과거에 계산된 gradient일 수록 작은 weight가 곱해진다.

momentum의 전반적인 효과는 trajectory를 smooth하게 만들고 valley (U자 와 같은 loss의 골짜기) 에서 oscillation 하는 것을 방지한다. 아래 Fig 6.7 을 보자

Fig 6.7: SGD with momentum. a) 일반 SGD은 minima로 향할 때 왔다 갔다 하는 (oscillation) 하는 성향을 보인다. b) SGD with momentum은 이전 방향을 고려하여 다음 진행 방향을 결정하므로 더 빠르게 minima에 도달한다. (빠른 convergence)

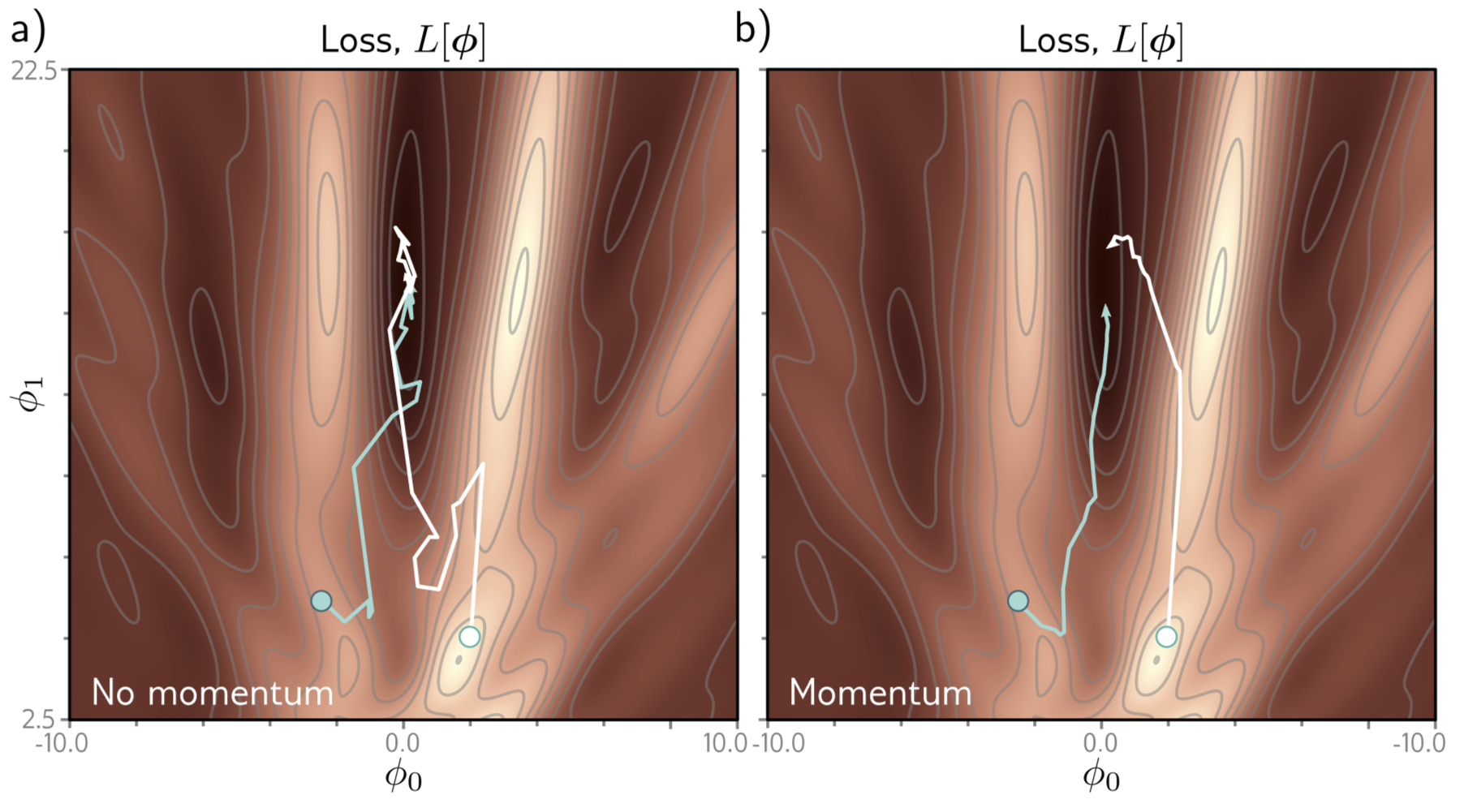
6.3.1 Nesterov Accelerated Momentum

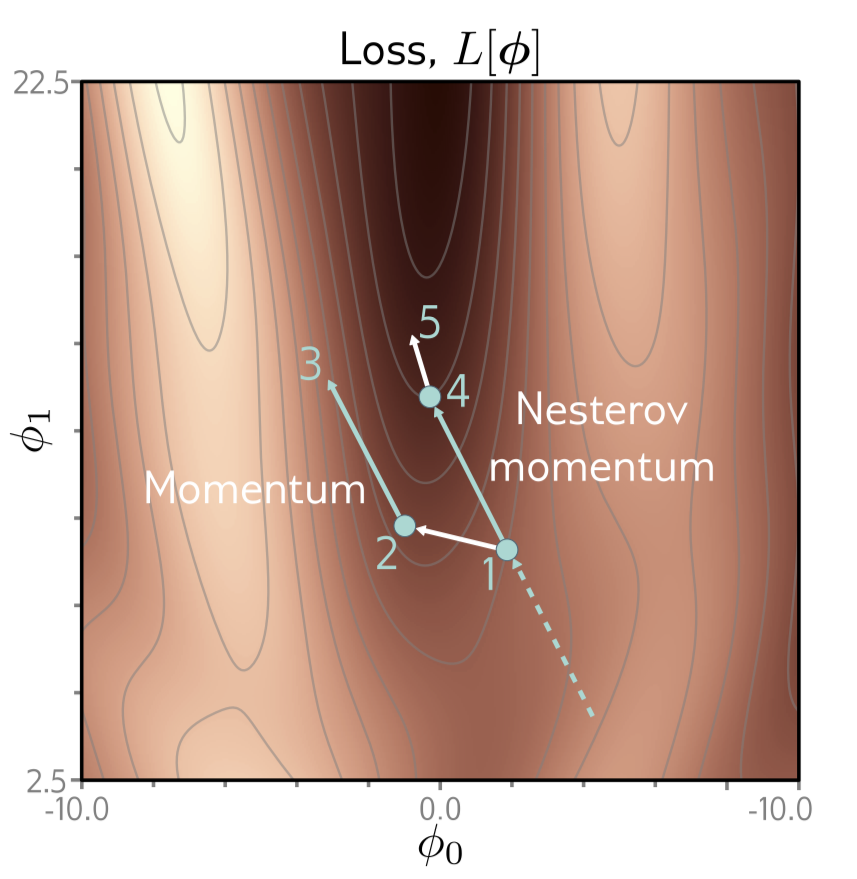
momentum term을 추가하는 것은 SGD 알고리즘이 다음에 어떤 방향으로 가야하는지 “예측”한다는 관점으로 볼 수 있다. 이러한 관점에서 Nesterov accelerated momentum은 이러한 예측을 현재 포인트가 아닌 다음 포인트에서 한다. (Fig. 6.8을 보라)

Fig 6.8: Nesterov Accelerated Momentum. 먼저 “- - -” 선을 따라 point 1에 도달한다. 기본적인 momentum 방법을 따르면 point 1에서 계산된 gradient (point 2) 에 이전 step의 방향을 weighted sum 하므로 point 2에서 point 1 로 향하는 방향을 더하게 된다. (point 3) Nesterov method는 point 1 에서 일단 왔던 방향으로 먼저 가고 (point 4) 여기서 gradient를 계산하여 더한다. (point 5)

업데이트 식은 아래와 같다.

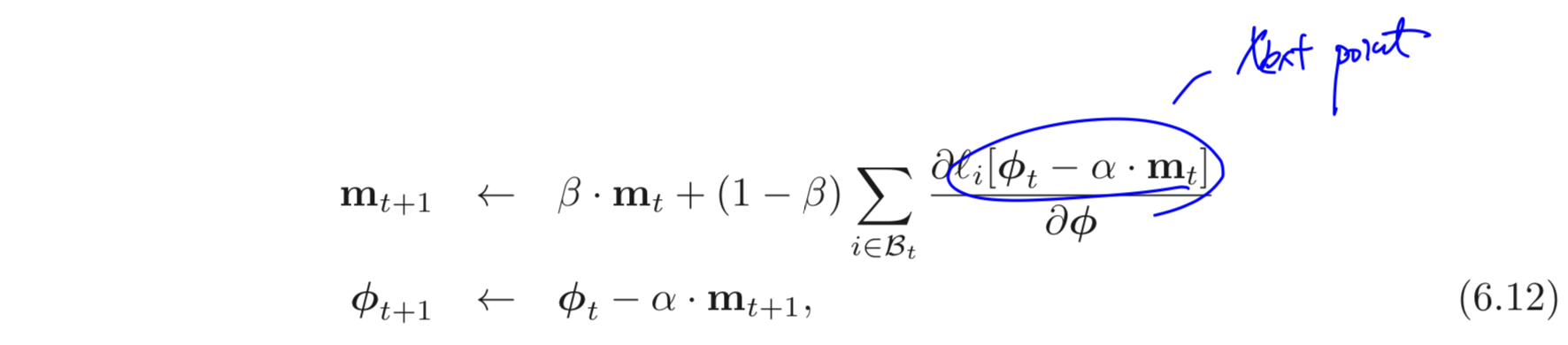
위 식을 보면 gradient가 $\phi_t - \alpha \cdot \bold{m}_{t}$ 에서 계산되는 것을 알 수 있다. Nesterov accelerated momentum 식을 바라보는 또 다른 관점으로는 기존의 momentum에서 gradient가 방향을 조절하는 것이라고 생각해볼 수 있다.

6.4 Adam

고정된 learning rate을 갖는 GD 알고리즘은 안좋은 특성들이 있다. 먼저, gradient의 크기와 다음 스텝으로 이동할 거리가 비례하다는 점이다. (gradient가 크면 멀리, 작으면 조금만 이동한다.) 그래서 만약에 loss function의 surface가 한 방향으로 너무 급하게 경사져있다면 학습이 안정적이지 않다는 문제가 있다. (Fig 6.9을 보라)

가장 직관적인 방법은 gradient를 normalize 하여 항상 같은 거리를 이동하게 하는 것이다. 이렇게 하기 위해서는 먼저 gradient, $\bold{m}_{t+1}$ 를 계산하고 각 elements를 제곱 (pointwise(=elementwise) square) 한 gradient, $\bold{v}_{t+1}$ 를 계산한다.

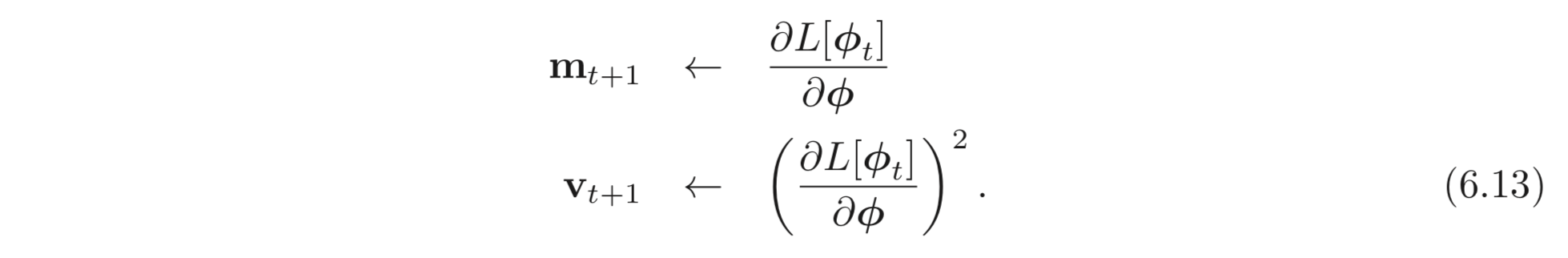
그리고 이를 update rule에 적용한다.

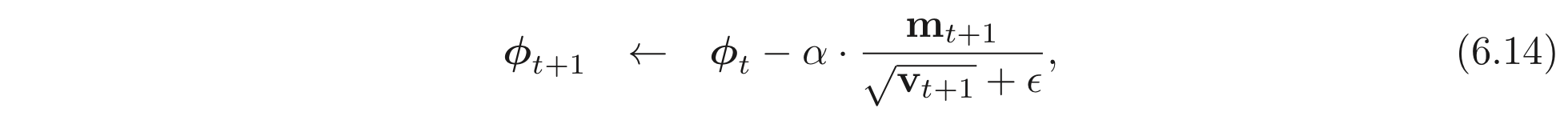
나눗셈도 각 element-wise하게 계산한다. $\epsilon$은 zero-by-division 문제를 막기위해 더하는 아주 작은 상수이다. 위와 같이 계산하면 $1, -1$ 만이 gradient로 계산된다. 이러한 normalized term 을 이용한 알고리즘은 꽤 괜찮은 학습 속도와 좋은 방향으로 나아갈 수 있겠지만 진짜 엄청 운이 좋게도 정확히 minima에 떨어지지 않는 이상 수렴할 수가 없다는 한계가 있다.

Adaptive Momentum Estimation, [Adam] 은 이러한 아이디어에서 출발하여 gradient와 squared gradient에 momentum을 더한다.

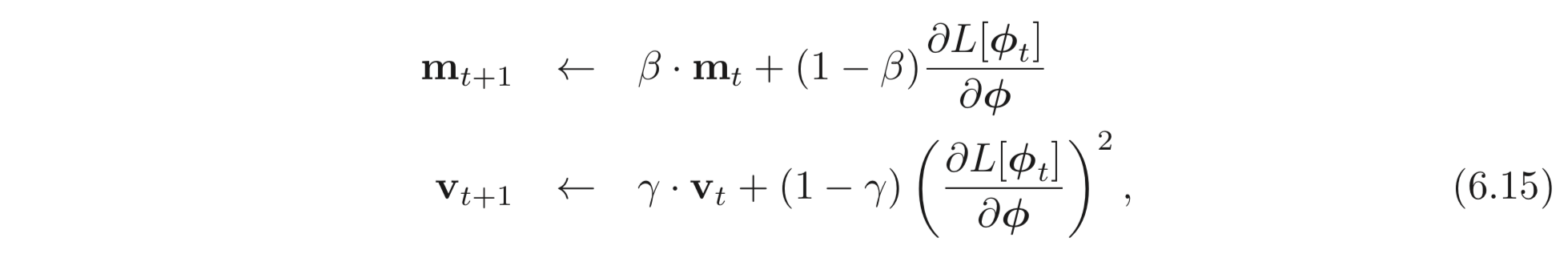
$\beta, \gamma$ 는 momentum coefficients이다. momentum을 사용한다는 것은 앞서 계산된 모든 값들에 대하여 weighted sum을 한다는 의미이다. 시작 과정에서는 모든 설정 값을 0으로 설정해둔다. 때문에 최종적인 weighted sum 값이 아주 작기 때문에 아래와 같은 식을 추가하여 실제 파라미터 업데이트에 쓰일 값들을 계산한다.

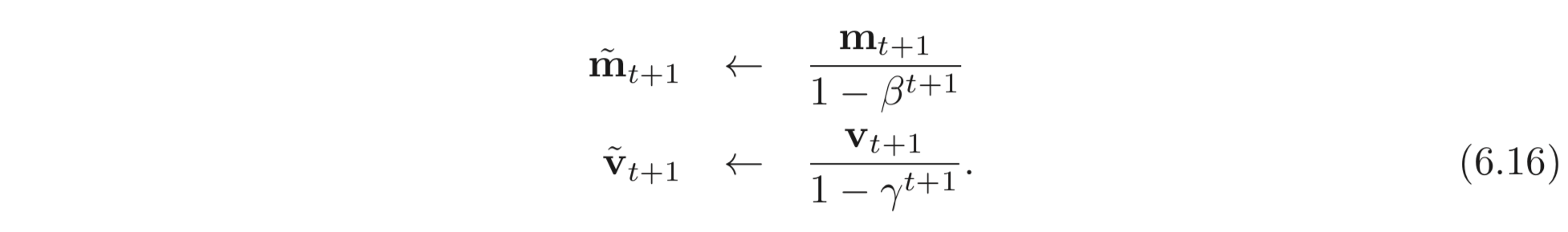
$\beta, \gamma \in [0, 1)$ 이므로 초반에는 작은 $\bold{m, v}$ 가 큰 값을 가질 수 있도록 몇 배 곱해주는 역할을 하고 time step, $t$가 커질 수록 $\beta^{t+1}, \gamma^{t+1} \rightarrow 0$ 으로 수렴하여 잘 estimate 된 gradient로 파라미터를 업데이트 할 수 있도록 한다. 최종적인 파라미터 업데이트 식은 아래와 같다.

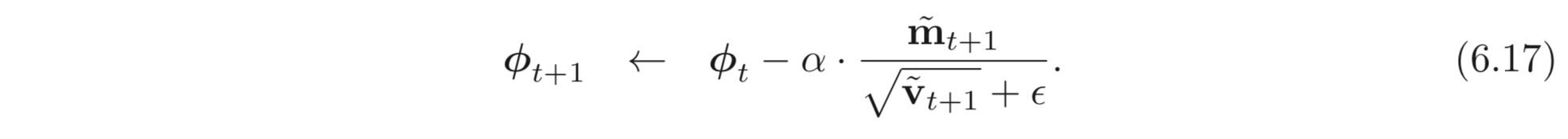
Adam은 global minima로 수렴할 수 있으며, 학습도 잘되는 편이다. Adam은 SGD의 방법으로 많이 사용되므로 batch 에 대한 estimates을 아래와 같이 계산할 수 있다.

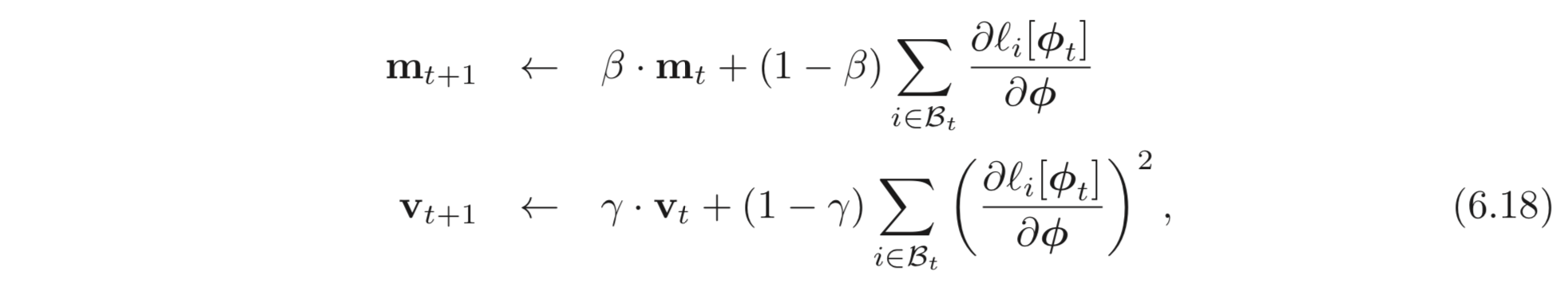
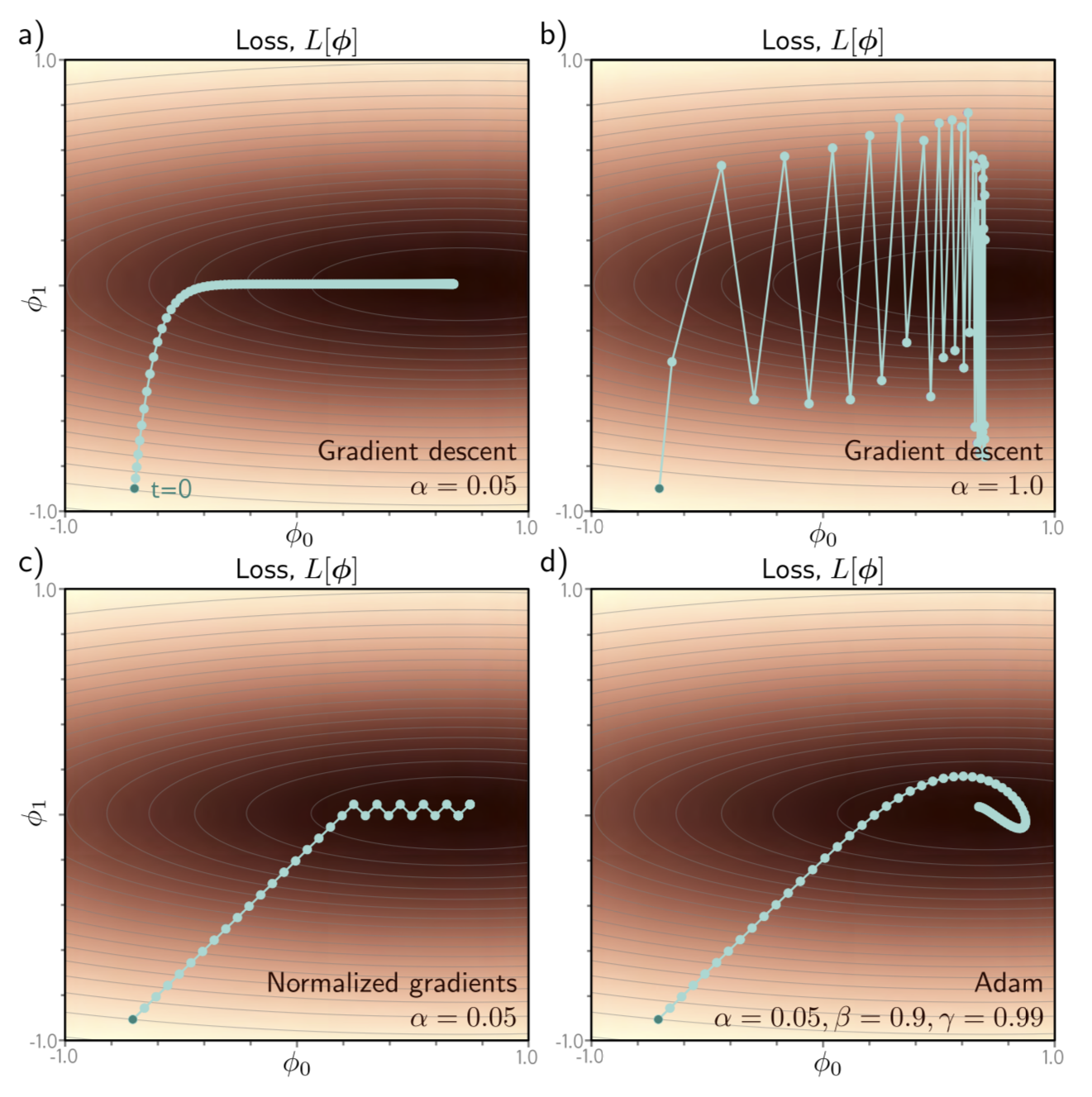
Fig 6.9: Adaptive momentum estimation (Adam). a) 수직으로는 빠르게 수렴하지만 수평 (valley) 을 이동할 때는 엄청나게 오래 걸리는 것을 알 수 있다.

b) learning rate이 클 경우, 수평으로 이동하는 과정에서 오버슈팅하는 것을 볼 수 있다. (학습이 불안정)

c) a, b) 와 같은 문제를 해결하는 방법으로 gradient의 크기를 그냥 고정시켜버리는 방법이 있다. 이러한 경우 oscillation도 크게 없고 학습도 빠르게 되겠지만 결정적으로 global minima에 도달할 수 없다는 한계가 있다.

d) Adam 알고리즘은 gradient와 nomalization term 모두에 momentum을 적용하여 더 smooth한 trajectory를 그린다.

앞으로 chapter 7에서 보겠지만, learning rate 는 뉴럴넷의 depth에 의존적이다. Adam은 이러한 경향을 보완하는데 도움을 줄 수 있고, 각기 다른 layers의 변화의 밸런스를 맞추는 것도 도움을 줄 수 있다. Adam은 또한 initial learning rate에도 덜 sensitive 한 장점이 있다. 그래서 복잡한 learning rate schedule이 없어도 된다는 장점이 있다.

6.5 Summary

모델을 학습하는 것은 파라미터, $\phi$ 에 대응하는 loss function, $L[\phi]$ 를 최소화하는 것으로 생각할 수 있다. Gradient Descent 는 현재 파라미터에서 계산되는 loss 지점에서의 uphill을 가리키는 gradient를 계산하고 이의 반대방향인 downhill ($\times -1$) 방향으로 파라미터를 업데이트 하였다.

non-linear function 에 대한 loss는 non-convex일 확률이 아주아주 높다. 따라서 local-minima나 saddle points를 포함할 수 있다. Stochastic Gradient Descent (SGD) 는 이러한 문제를 어느 정도 해결할 수 있다.

SGD는 학습 데이터에서 중복을 허용하지 않게 몇몇 examples 를 샘플링한다. 이들을 batch 혹은 minibatch 라고 한다. 이 batch에 대하여 loss와 gradient를 계산한다. 이러한 접근은 gradient에 noise를 더한다고 볼 수 있고 이러한 과정에서 앞선 local minima, saddle points를 피하도록 한다.

마지막으로 이러한 SGD 알고리즘에 momentum term 을 추가하는 것이 학습을 효과적으로 도울 수 있음을 보았고, Vanilla momentum, Nesterov Accelerated momentum, Adaptive Momentum Estimate (Adam) 까지 살펴보았다.

Uploaded by N2T