Loss functions

본 포스팅은 Simon J.D. Prince 의 Deep Learning 교재를 스터디하며 정리한 글임을 밝힙니다.

https://udlbook.github.io/udlbook/

앞선 3개의 챕터에서는 linear regression, shallow network 그리고 deep network에 대해 공부했다. 각 챕터에서 input과 output을 맵핑하는 family of functions를 살펴보았고, 각 family of functions는 파라미터 $\phi$ 에 의해 결정된다. 이러한 모델들을 학습하는 것은 우리가 풀고자 하는 문제에 대하여 가능한 최선의 “input → output”을 맵핑하는 파라미터 $\phi$를 찾는 것이다. 본 챕터에서는 “best possible” 맵핑이 의미하는 것이 무엇인지를 정의한다.

이러한 정의는 input/output pair가 있는 훈련데이터, $\{ \bold{x_i, y_i} \}$ 가 필요하다. loss function 혹은 cost function, $L[\phi]$는 학습시키는 모델의 prediction, $\bold{f[x_i, \phi]}$와 이에 대응하는 ground-truth, $\bold{y_i}$ 가 얼마나 서로 “다른지”에 대한 값을 return한다. 학습 중에는, 학습 데이터의 input과 output의 맵핑을 가능한한 loss가 최소가 되도록하는 파라미터 $\phi$를 찾는다. 챕터2에서 MSE Loss를 보았는데 이게 왜 적절한 함수였는지를 살펴본다.

본 챕터는 $\R$(실수)를 갖는 출력에 대하여 왜 MSE를 사용했는지에 대해 설명하고 다른 타입의 prediction에 대한 loss function을 설계하는 방법을 제공하는 framework을 제공한다.

Take Home

1. 모델이 입력, $\bold{x}$를 받아서 출력, $\bold{y}$를 직접 계산하는 관점에서 출력에 대한 “확률 분포”를 예측하는 관점으로 옮긴다. 정리 하자면, 출력 space에서 정의된 확률 분포, $Pr(\bold{y|\theta})$ 의 파라미터, $\theta$를 예측하는 모델, $\theta = f[\bold{x, \phi}]$ 를 설계한다.

2. 확률 분포의 관점에서 출력을 해석하기 때문에 자연스럽게 모델을 학습하는 것은 likelihood 를 최대화하는 방향으로 생각할 수 있다. 하지만 편의상, loss를 minimize 하는 것이 일반적이기 때문에 $-1$을 곱하여 negative log-likelihood 를 최소화하여 모델을 학습한다.

   이는 loss를 최소화 한다는 점에서 언어적으로 conventional 할 뿐만 아니라 precision이 제한되는 컴퓨터에서 계산상 정확도에서 이점이 있다.

3. 이러한 흐름에서 자연스럽게 MSE Loss가 negative log-likelihood criterion의 일종이라는 것을 유도하였고, 여기에는 variance가 동일하다는 가정이 있다는 것을 수학적으로 보인다. variance 가 상수인 모델을 homoscedastic 하다고 하며, variance가 입력에 따라 다른 모델을 heteroscedastic 하다고 한다.

4. 다양한 출력, 다양한 tasks 에 대하여 loss function을 설계하는 framework을 공부한다.
   1. output space에 적절한 probability distribution을 선택한다.
   2. probability distribution의 파라미터, $\theta$ 중 어떤 값을 예측할지 설정하고, 이를 예측하는 모델, $\bold{f}[\bold{x}, \phi]$ 를 설계한다.
   3. Negative log-likelihood를 적용한다.
   4. 출력은 maximum을 return 할 수도, 확률 분포 자체를 return 할 수도 있다.

5. 마지막으로 Cross-Entropy Loss와 Negative log-likelihood criterion이 본질적으로 equivalence 하다는 것을 수학적 보인다.

5.1 Maximum Likelihood

5.1에서는 loss function을 설계하기 위한 기초 단계를 공부한다. 모델 $\bold{f[x, \phi]}$ 를 생각해보자. 지금까지는 input $\bold{x}$에 대하여 prediction, $\bold{y}$를 “직접” 계산하였다. 지금부터는 우리의 관점을 옮겨 모델을 input $\bold{x}$ 가 주어졌을 때 가능한 출력 $\bold{y}$에 대한 conditional probability, $Pr(\bold{y_i}|\bold{x_i})$ 를 계산하는 것으로 본다.

5.1.1 Computing a distribution over outputs

이러한 관점은 “도대체 어떻게 모델이 확률 분포를 계산하는데?” 라는 질문을 낳는데 대답은 간단하다.,

1. parametric distribution, $Pr(\bold{y|\theta})$ 를 선택한다.

2. 그리고 우리의 “모델”이 저 $\theta$를 예측하도록 한다.

예를 들어, 우리의 prediction 하고자 하는 출력의 domain이 실수라고 해보자 ($y \in \R$). 여기서 우리는 univariate normal distribution (고등학생 때 배우는 일변수 가우시안 분포) 을 선택할 수 있다 (step 1). 이러한 분포는 $\mathcal{N}(\mu, \sigma^2)$ 와 같이 나타내어진다. 모델은 이러한 mean, $\mu$와 variance, $\sigma$만을 예측하면 된다 (step 2).

5.1.2 Maximum Likelihood Criterion

5.1.1에서 보았던 관점에 따라 이제 모델은 입력, $\bold{x_i}$에 대하여 각기 다른 분포의 파라미터, $\bold{\theta_i = f[x_i, \phi]}$ 를 계산하는 것으로 볼 수 있다. 학습 데이터에 있는 $\bold{y}_i$는 이에 대응하는 distribution, $Pr(\bold{y}_i|\theta_i)$ 에 대하여 높은 probability를 가져야한다. 따라서 모든 학습 데이터에 대하여 combined probability가 최대가 되도록하는 파라미터, $\phi$를 찾아야한다.

combined probability, $\displaystyle\prod_{i=1}^{I}Pr(\bold{y}_i|\bold{x}_i)$ 를 파라미터, $\theta$에 대한 likelihood라고 한다. 따라서 위 Eq. 5.1는 maximum likelihood criterion 이라고 알려져있다. 위 식은 두 가지 가정 아래서 성립한다.

💡

conditional probability, $Pr(z|\psi)$ 는 두 가지 방법으로 해석된다. 하나는 $z$에 대한 함수다. 이러한 관점에서 확률 분포의 합은 1이다. 다른 방법은 $\psi$에 대한 함수로 보는 것이다. 이러한 관점이 likelihood로 알려져 있으며 보통 확률 분포의 합이 1이 아니다.

1. 데이터가 identically distributed 하다. (각 데이터 포인트에 대하여 출력, $\bold{y}_i$개 대한 확률 분포의 “모양”이 똑같다.)

2. 입력이 주어졌을 때 출력에 대한 conditional distribution, $Pr(\bold{y}_i| \bold{x}_i)$ 가 independent 하다.

다른 말로 이러한 두 가정을 합쳐, independent and identically distributed, $i.i.d$ 라고 한다. 학습 데이터의 총 likelihood는 아래와 같이 계산된다.

$$Pr(\bold{y_1, y_2, ..., y_I|x_1, x_2, ..., x_I}) = \displaystyle\prod_{i=1}^{I}Pr(\bold{y}_i|\bold{x}_i)$$

5.1.3 Maximizing log-likelihood

앞선 Eq. 5.1 과 같은 maximum likelihood는 전혀 실용적이지 못하다. 각 term, $Pr(\bold{y}_i|\bold{f}[\bold{x}_i|\phi])$ 는 작은 값을 보통 갖고, 이러한 값을 여러번 곱하면 아주아주 작아질 것이다. 이러한 값을 컴퓨터와 같은 제한적인 precision을 갖는 머신에서 표현하는 것은 쉽지 않은 일이다. 다행히도, 우리는 likelihood의 log를 씌운 값을 maximize해도 똑같은 결과를 얻을 수 있다.

이러한 log-likelihood criterion은 log함수가 단조 증가 함수 (monotonically increasing function) 이기 때문에 likelihood criterion과 동일 (equivalence) 하다. 이러한 성질로 인해 몇 가지 이점을 갖는다.

1. 오리지널 likelihood에서의 최댓값을 갖는 점과 log-likelihood에서 최댓값을 갖는 점이 갖기 때문에 log-likelihood에서 찾은 최적의 파라미터, $\hat{\phi}$ 는 오리지널 likelihood에서도 최적의 파라미터이다.

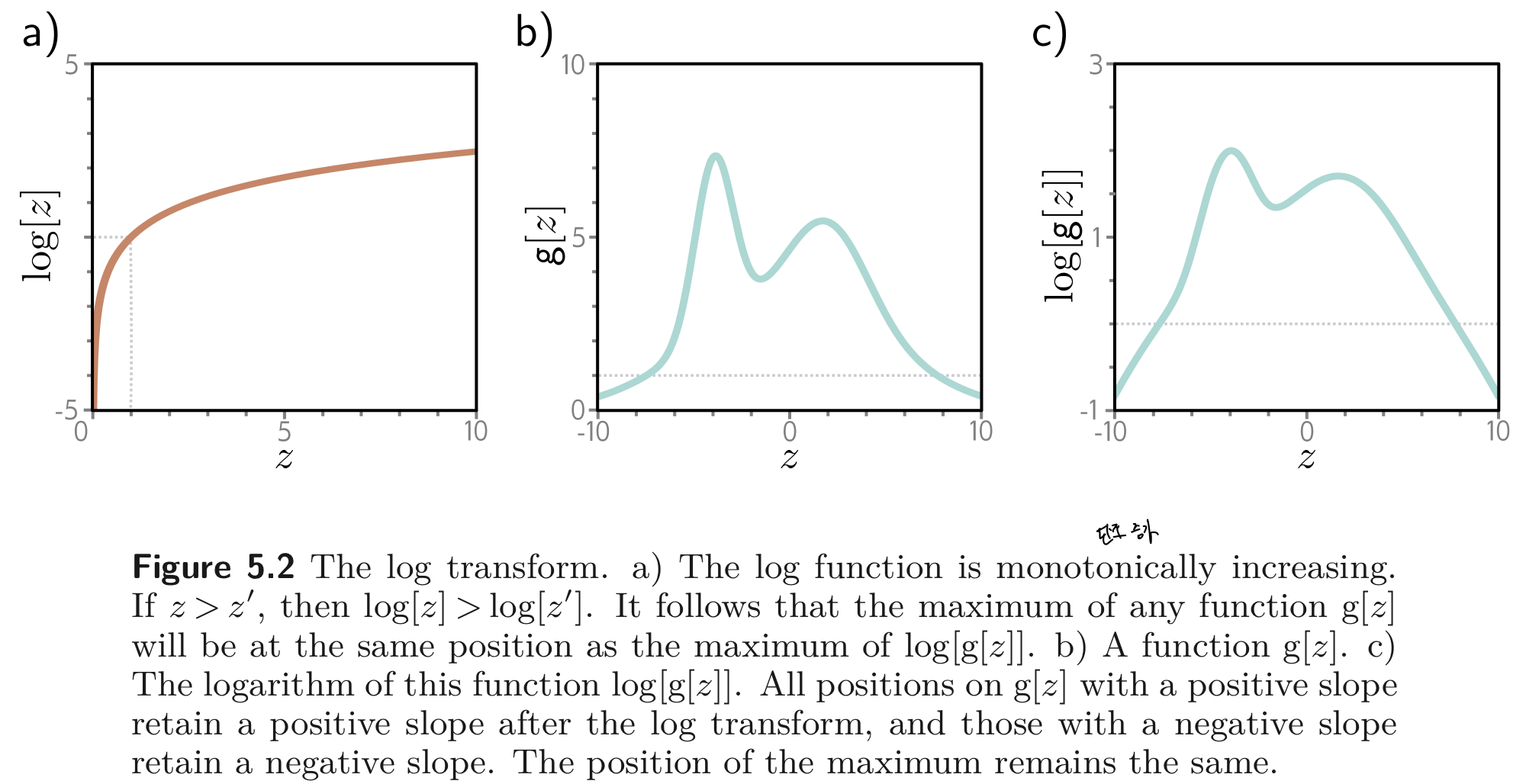
2. 곱으로 이루어진 식을 덧셈으로 바꿀 수 있으므로 제한된 precision을 갖는 컴퓨터에서 더 실용적으로 사용될 수 있다. (Eq. 5.3 에서 2번째와 3번째 식을 보라.)

5.1.4 Minimizing Negative log-likelihood

마지막으로 보통 (by convention), 모델을 피팅한다는 것은 대부분 loss를 최소화 한다는 틀에 박혀있다. 따라서 maximum log-likelihood criterion을 minimizing 하는 문제로 변환하기 위해서는 그저 $-1$ 을 곱해주면 된다. 우리는 이것을 negative log-likelihood criterion 이라고 한다.

최종적으로 아래와 같은 Loss 식을 얻는다.

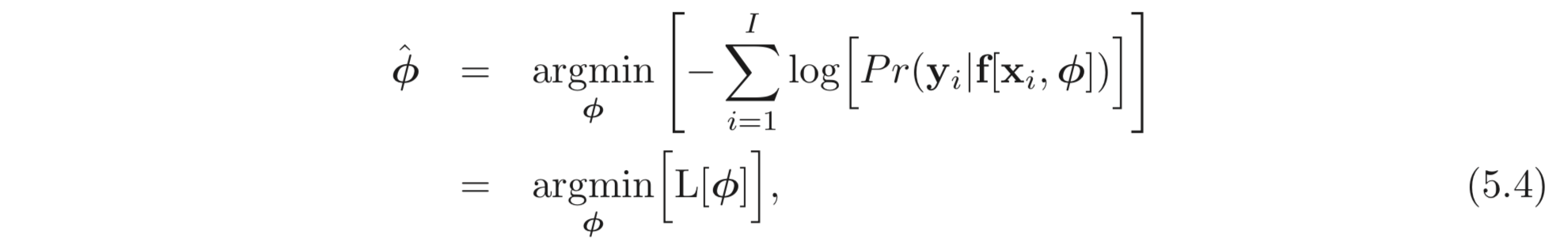
5.1.5 Inference

앞선 섹션들에서 모델은 더 이상 $\bold{y}$를 직접 계산하지 않고 대신 $\bold{y}$에 대한 확률 분포를 결정하는 값들을 계산한다. 추론시에는 확률 분포가 아니라 어떤 점, point를 얻고 싶은 경우가 많다. 이러한 경우에는 확률 분포의 최댓값을 return한다.

이런 경우 보통 확률 분포의 파라미터, $\theta$에서 그 값을 찾아볼 수 있다. 예를 들어, univariate normal distribution에 대해서는 평균, $\mu$에서 최댓값을 찾을 수 있다.

5.2 Recipe for Constructing Loss Functions

정리하자면, 훈련 데이터, $\{ \bold{x}_i, \bold{y}_i \}$ 에 대한 loss function을 maximum likelihood approach로 설계하는 레시피는 아래와 같다.

1. 적절한 확률 분포, $Pr(\bold{y|\theta})$ 를 선택한다. 여기서 확률 분포는 출력, $\bold{y}$의 정의역 위에서 정의되며 확률 분포의 파라미터, $\bold{\theta}$를 갖는다.

2. 확률 분포의 파라미터, $\theta$의 어떤 값을 사용할지 결정하고 그 값들을 예측 하도록 모델, $\bold{f[x, \phi]}$ 를 설계한다. ($\theta=\bold{f[x, \phi]}$ 이고, $Pr(\bold{y|\theta}) = Pr(\bold{y|f[x,\phi]})$ 가 되도록.)

3. Negative log-likelihood를 최소화하는 모델 파라미터, $\hat{\phi}$를 찾는다.

   

4. 새로운 데이터, $\bold{x}$에 대하여 inference를 할 때는 확률 분포, $Pr(\bold{y}|\bold{f}[\bold{x}_i|\phi])$ 를 return하거나 이 분포의 최댓값을 return 한다.

5.3 Example 1: Univariate Regression

univariate regression (일변수 회귀) 모델로 먼저 시작해보자. 목표는 입력, $\bold{x}$를 받고 파라미터, $\phi$를 갖는 모델, $\bold{f}[\bold{x, \phi}]$를 사용하여 scalar 출력, $y \in \R$을 예측하는 것이다. 앞서 5.2 에서 공부한 레시피에 따라서

1. 출력 도메인, $y$에 대한 확률 분포를 선택한다. 본 섹션에서는 univariate normal distribution을 선택한다.

univariate normal distribution은 실수에서 정의되며, 두 개의 파라미터, $\mu, \sigma^2$ 를 갖고 PDF를 갖는다. 식은 아래와 같이 나타내어진다.

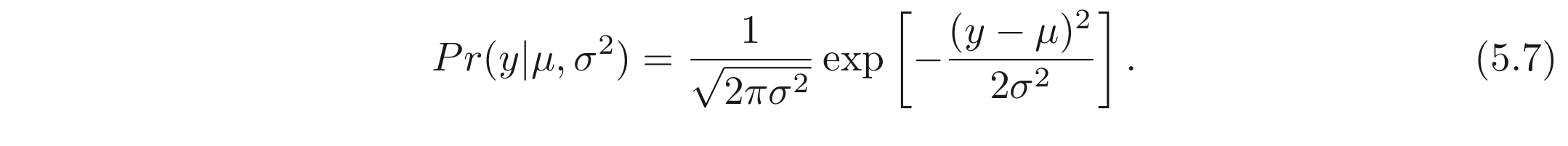
2. ML model, $f[\bold{x}, \phi]$가 앞선 확률 분포의 파라미터 중 하나를 예측하게 한다. 여기서는 평균, $\mu$만을 예측하도록 한다.

3. 모델을 학습할 때는, 편의를 위해 negative log-likelihood 에 기반한 loss 함수를 정의한다.

5.3.1 Least Squares Loss Function

앞서 정의한 loss 함수에서 약간의 과정을 거치면 다음과 같은 식을 얻을 수 있다.

첫번째 식에서 두 번째 식으로 가는 과정은 $log[ab] = log[a] + log[b]$ 의 성질을 이용하여 $exp$ 앞에 상수와 $exp$ 식을 분리하고, $ln[e^{a}] = a$ 의 성질을 이용하여 지수항만을 남긴 것이다. 두 번째에서 세 번째 식으로 가는 과정에서는 앞선 $log[\frac{1}{\sqrt{2\pi\sigma^2}}]$ 는 $\phi$와 관련이 없으므로 생략한 것이고, 3→4 번째 식의 과정에서도 deniminator(분모), $2\sigma^2$ 도 $\phi$와 관련이 없으므로 생략된다.

결과적으로 chapter2 에서 사용했던 MSE Loss를 얻을 수 있다.

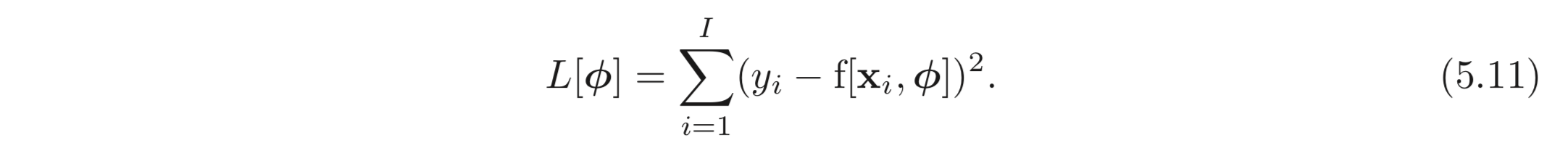
앞서 scalar, $y$를 예측하기 위해 $y$에서 정의되는 univariate normal distribution을 파라미터, $\mu, \sigma$ 로 나타내었다. 여기서 파라미터 중 평균, $\mu$만을 예측하는 모델을 정의하고 이에 대한 negative log-likelihood를 정의하였다. 그리고 이 loss 함수로 부터 MSE Loss를 유도하였다.

따라서 MSE Loss는 자연스럽게 다음과 같은 가정을 내포하는 것을 알 수 있다.

1. 각 prediction errors, ($(y_i-f[x_i, \phi])$) 가 independent 하다는 것.

2. 그리고 prediction errors가 평균, $\mu=f[\bold{x}_i, \phi]$ 을 갖는 normal distribution으로부터 계산된다는 것이다.

Figure 5.4: MSE Loss와 maximum likelihood loss와의 같음 (equivalence) 을 보임. a-b)는 MSE Loss이며, c-d)는 negative log-likelihood이다. 둘 다 작을 수록 좋다. a, c)는 잘 피팅됐기 때문에 작지만 b, d)는 잘 피팅 되지 않았기 때문에 큰 값을 갖는다.

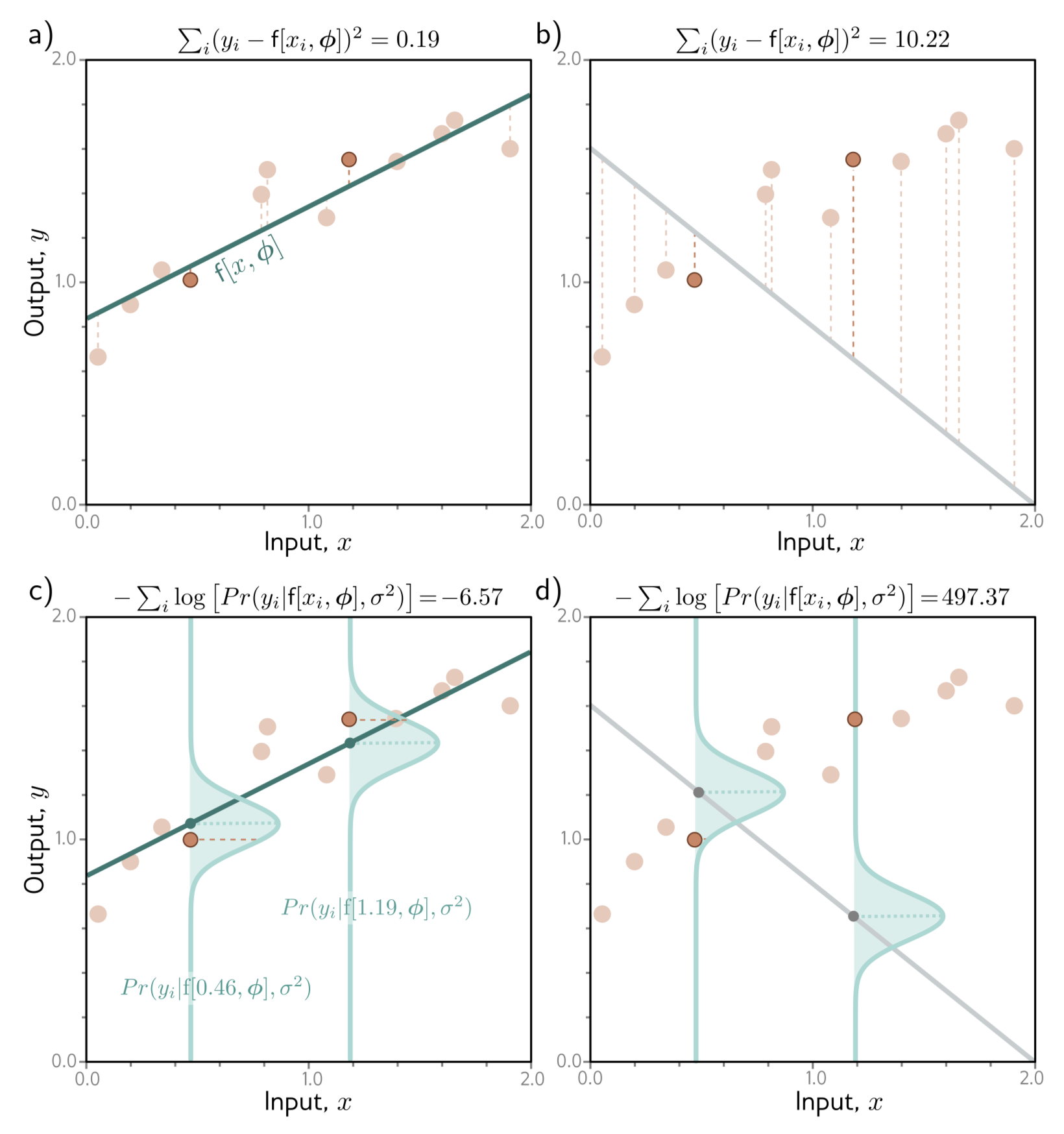
5.3.2 Inference

모델은 더 이상 $y$를 직접 계산하지 않고 대신 $y$에서 정의된 normal distribution의 평균, $\mu= f[\bold{x}, \phi]$를 계산한다. inference 시에서는 주로 “best” point, $\hat{y}$를 알고 싶다. 따라서 예측된 분포의 최댓값을 최종 결과로 갖는다.

예를 들어, Univariate normal 에 대해서는 최댓값을 갖는 지점이 평균, $\mu$에 의해 결정된다. 이는 모델의 출력 결과이므로, 이 경우, $\hat{y}=f[\bold{x}, \phi]$ 이다.

5.3.3 Estimating Variance

MSE Loss를 유도하기 위해 모델이 normal distribution의 mean, $\mu$만을 예측하도록 하였다. Eq. 5.11 을 보면, $\sigma^2$에 대하여 무관하다. 하지만 $\sigma^2$ 에 대하여 고려하지 않을 이유가 전혀 없다. 아래와 $\phi, \sigma^2$ 모두에 대하여 loss 값이 최솟값이 되는 지점을 찾을 수 있다.

이러한 경우 inference 시에는 모델이 그대로 $\hat{y}=f[\bold{x}, \phi]$ 를 예측하면 되고, $\sigma^2$은 해당 결과에 대한 uncertainty가 된다.

5.3.4 Heteroscedastic Regression

앞선 예제에서는 모두 variance가 상수였다. 하지만 이는 현실적이지 않을 수 있다. 입력 데이터에 따라 모델의 uncertainty가 달라지면 이를 heteroscedastic 하다. 라고 한다. (반대는 homoscedastic.)

Figure 5.4: a-b)는 homoscedastic, c-d)는 heteroscedastic 한 모델이다.

이러한 모델을 학습한 방법은 모델, $\bold{f}[\bold{x, \phi}]$ 가 mean, variance, 둘 다를 예측하도록 하면된다. 간단히 두 개의 SNN을 생각해보면 된다 ($\bold{f}_1[\bold{x}, \phi], \bold{f}_2[\bold{x, \phi}]$). 그런데 여기에는 variance는 항상 양수여야 한다는 문제가 있다. 이를 해결하기 위해 임의의 값을 양수로 만들어주기 위한 함수에 먹인다. 간단한 방법은 제곱을 하는 것이다.:

이러한 경우 최종 loss 함수는 아래와 같이 정의된다.

5.4 Example 2: Binary Classification

binary classification 에서는 두 개의 discrete classes를 갖는 $y \in \{0, 1\}$ 을 입력, $\bold{x}$에 대해 할당 하는 task이다. 이러한 관점에서 $y$를 label 이라고 한다. Binary classificaion의 예로는 식당의 호불호를 예측하거나 종양의 양성/음성을 판단하는 tasks가 있다.

또다시 5.2의 loss 함수를 설계하는 레시피를 따라가보자.

1. 출력 도메인(space) ($y \in \{0,1\}$) 에 대한 적절한 확률 분포를 선택한다. 본 예제에서는 Bernoulli distribution이 적절하다.

   

   

2. 모델, $f[\bold{x}, \phi]$가 베르누이 분포의 파라미터, $\lambda$를 예측하도록 설계한다. 하지만 $\lambda$는 $[0,1]$에서만 정의된다. 따라서 우리는 $\R \rightarrow[0,1]$ 을 맵핑하는 적절한 함수에 모델의 예측값을 먹여야한다. 이 경우 logistic sigmoid 함수가 적절하다.

   

   따라서 확률 분포의 파라미터, $\lambda = sig[f[\bold{x, \phi}]]$ 를 구할 수 있고, likelihood는 아래와 같이 계산된다.

   

3. Negative log-likelihood를 적용한다. (log 씌우고 -1 곱.)

   

   5.7 섹션에서 설명할 이유로 인해, 이 loss는 Binary Cross-Entropy Loss 라고 알려져 있다 (BCELoss in Pytorch). $sig[f[\bold{x}, \phi]]$ 는 $\lambda$를 예측하고 이는 $y=1$을 확률을 나타낸다. 따라서 inference를 할 때는 $y=1, \text{ if }\lambda > 0.5 \text{ else, } y = 0$ 이다.

Figure 5.8: Binary classification model. a) 의 결과가 b)를 거쳐 c)로 맵핑되었다. 맵핑된 값은 lambda 를 의미하므로 0.5 이상은 y=1, 다른 경우엔 y=0이다.

5.5 Example 3: Multiclass Classification

Multiclass classification은 입력 데이터, $\bold{x}$에 대하여 $K>2$의 classes를 할당하는 task이다. MNIST, 주어진 문장 뒤에 올 다음 단어를 예측하는 것이 예시가 된다.

여기서도 5.2의 레시피를 사용한다.

1. $y$ space 에 대한 적절한 분포를 찾는다. 여기서는 categorical distribution이 된다.

   

2. 모델은 모든 파라미터, $\lambda_1, \lambda_2, ..., \lambda_K$를 예측하도록 설계한다.

   이는 $K$개의 파라미터, $\lambda_1, \lambda_2,...,\lambda_K$를 갖는다.

   

   이들은 $\lambda_1 + \lambda_2 + ... + \lambda_K = 1$ 이라는 constraint를 갖는다. 모델은 $\R^K$ 의 출력을 가지므로 앞선 constraint를 만족시키는 함수에 출력을 먹여야하는데 적절한 함수로는 softmax 함수가 있다.

   

   exponential term은 양수를 보장하기 위함이고, 분모는 합이 1이 되도록 하기 위함이다. 아래는 예시 그래프이다.

   

   입력, $\bold{x}$가 label $y$를 가질 likelihood는 띠라서 다음과 같이 정의된다.

   

3. Negative log-likelihood를 적용한다.

   

   $i$번째 label, $y_i$ 에 대한 likelihood 에 대해서만 loss를 계산한다. MNIST 예제를 예로 들어보자. 그러면 모델의 출력, $y \in \R^{10}$ 이다. (1, 2, 3, 4, 5, 6, 7, 8, 9, 0) sigmoid를 통과시킨 결과, $sig[y] \in \R^{10}$ 이다. 5라고 적힌 글자가 입력으로 들어왔다면, 모델은 10개의 파라미터, $\lambda_1, \lambda_2, ..., \lambda_{10}$ 에 대해서 계산을 하고. 이를 sigmoid 함수에 먹인다. 그러면 여기서 정답, $y_i$는 5이므로, 5번째 결과인, $\frac{e^{\lambda_5}}{e^{\lambda_1}+e^{\lambda_2}+...+e^{\lambda_{10}}}$ 가 모델이 예측한 likelihood, $Pr(y=5|\bold{x})$가 된다.

   Eq. 5.24와 비교하면, 첫 번째 식에서 $softmax_{y_i}$ 는 5가 적힌 글자의 이미지를 예로 들면, $softmax_5$ 의 값이 될 것이다. 이의 결과는 $\frac{e^{\lambda_5}}{e^{\lambda_1}+e^{\lambda_2}+...+e^{\lambda_{10}}}$ 이며, log를 씌우면, ($log[\frac{a}{b}] = log[a]-log[b]]$) 두 번째 식이 나온다.

   5.7 섹션에서 설명할 이유로 이 또한 multiclass cross-entropy loss 라고 알려져있다.

   입력에 대한 label, 즉 예측점을 찾기 위해 (point estimate) $\hat{y} = \displaystyle\argmax_k[Pr(y=k|\bold{f[x, \phi]})]$ 를 선택할 수 있다.

5.5.1 Predicting other data types

가능한 다른 도메인에 대해서 사용할 수 있는 확률 분포를 표로 정리하였다.

5.6 Multiple Outputs

동일한 모델로 여러 값을 예측하고자 하는 경우가 많다. 이러한 경우 출력은 벡터의 형식, $\bold{y}$의 폼을 갖는다. 예를 들어 분자의 어는 점과 끓는 점을 모두 알고 싶을 때도 있고, 이미지의 모든 점에서 각 점의 class를 알고 싶은 경우도 있다. 이러한 경우 multivariate probability distribution을 사용하여 모델을 설계할 수도 있지만, 주로 이들을 모두 independent 하다고 가정하고 문제를 해결하는 것이 일반적이다.

Independence는 probability, $Pr(\bold{y|f[x, \phi}])$ 를 모든 elements, $y_d \in \bold{y}$의 모든 product로 여긴다는 것을 암시한다 (Eq. 5.25).

$\bold{f}_d[\bold{x}_i, \phi]$ 는 $y_d$의 확률 분포의 파라미터를 나타낸다. 예를 들어 $y_d \in \R$ 이라면, 각각의 $y_d$에 대한 확률 분포의 파라미터를 따로따로 예측하며, 만약 multiclass classification을 한다면, $y_d$를 예측하기 위해 10개의 파라미터를 “각각” 예측한다는 뜻이다.

💡

semantic segmentation 을 예로 들어보자. 만약 풀밭 위에 송아지가 있다면 송아지가 있는 각각의 픽셀들이 있을 것이고, 풀이 있는 픽셀들이 있을 것이다. 이들을 모두 “각각” 예측하여 각 픽셀의 “송아지가 있을 확률”, 과 “풀이 있을 확률”을 독립적으로 구한다는 것이다.

따라서 아래 negative log-likelihood loss term을 최소화 하면 된다.

기존의 식과 전혀 다르지 않다. 기존의 식은 단지 $d=1$이었을 뿐이다.

다시 한 번 강조하자면 이렇게 한 번에 여러 결과를 추론하고자 한다면, 각각의 error가 independent 하다는 가정이 있어야한다.

5.7 Cross-Entropy Loss

본 섹션에서는 negative log-likelihood를 최소화하는 loss 함수를 공부한다. cross-entropy loss 로도 널리 사용되는 단어이다. 먼저 cross-entropy loss 에 대해 공부하고 negative log-likelihood를 사용하는 것과 동일하다는 것 (equivalence) 을 보인다.

cross-entropy loss는 training data의 $y$로 부터 구해지는 empirical distribution, $q(y)$ 와 예측한 model distribution, $Pr(\bold{x}, \theta)$ 간의 distance 를 최소화하는 파라미터, $\theta$를 찾는다는 아이디어에서 출발한다. 두 확률 분포, $p(z), q(z)$ 간의 distance는 Kullback-Leibler (KL) divergence 로 계산될 수 있다.

출력, $y$는 $\{ y_i \}_{i=1}^I$ 와 같이 points로 존재하므로, 이를 Dirac delta 함수, $\delta[\bullet]$ 을 사용하여 나타낼 수 있다.

Dirac delta 함수는 적분하면 1이며, 딱 point에만 존재한다. 이를 그래서 그래프 상에 나타낼 때는 화살표로 나타낸다. empirical distribution (GT) 와 model distribution 간의 KL divergence를 최소화 한다.

첫 번째 식의 왼쪽 term이 두 번째 식에서 날아가는데 이는 $\theta$에 종속적이지 않기 때문이다. 두 번째 식에서 남은 이 식은 cross-entropy를 구하는 식으로 알려져 있다. 이는 우리가 어떤 확률 분포를 알고 있을 때, 이와 비교하는 다른 확률 분포에 남은 uncertainty의 양을 의미한다고 해석할 수 있다.

Eq. 5.29의 식에서 $q(y)$를 Eq. 5.28 로 대체하면 아래와 같은 식을 얻을 수 있다.

각 줄의 식이 의미하는 바는 아래와 같다.

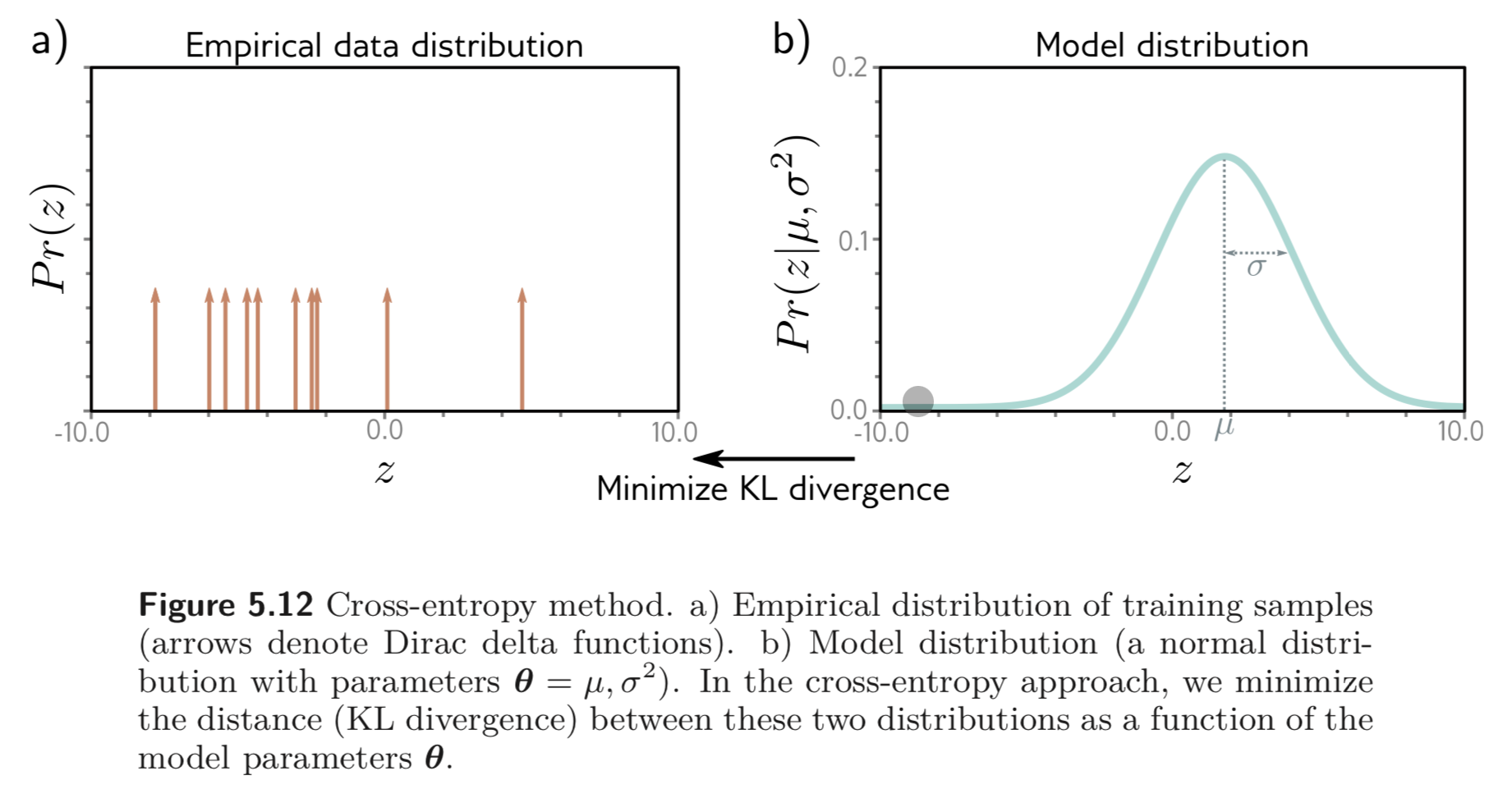
1. Eq 5.30의 첫 번째 식은 Fig. 5.12 a) 에 표현된 dirac delta 함수와 b)에 log를 씌운 값이 pointwisely 곱해진다.

2. 그러면 남은 식은 dirac delta 함수에 곱해진 유한한 weighted probability masses이다.

3. 마지막 식은 $\frac{1}{I}$는 $\theta$에 종속되지 않으므로 제거한다.

$\theta$, 즉 확률 분포의 파라미터는 모델, $\bold{f}[\bold{x}_i, \phi]$에 의해 계산되므로 최종식은 아래와 같이 나타낼 수 있다.

이는 정확히 negative log-likelihood criterion과 동일하다. 정리하자면 cross-entropy loss와 negative log-likelihood criterion은 equivalence 하다.

끝.

Uploaded by N2T