K-Means 병렬처리: cs149 실습 예제 1-6번 문제

GitHub - stanford-cs149/asst1: Stanford CS149 -- Assignment 1

Stanford CS149 -- Assignment 1. Contribute to stanford-cs149/asst1 development by creating an account on GitHub.

https://github.com/stanford-cs149/asst1#program-3-parallel-fractal-generation-using-ispc-20-points

문제 설명

본 과제는 K-Means clustering algorithm을 사용해서 100만개의 데이터 포인트들을 클러스터링 하는 프로그램을 다룬다.

What is K-Means?

label이 있는 데이터셋, $\{x_i, y_i\}_{i=1}^{N}$ 간의 mapping 관계를 학습하는 Supervised learning과는 다르게 label이 없는 데이터셋, $\{x_i\}_{i=1}^{N}$ 이 주어졌을 때 이러한 데이터를 학습하는 가장 직관적인 방법은 비슷한 녀석들끼리 모아 이들을 grouping 하는 것이다. 이러한 group들을 앞으로 Cluster 라 한다.

K-Means는 clustering 알고리즘 중 가장 널리 사용되는 알고리즘 중의 하나이다. K-Means는 각 clusters를 정의하는 $k$ 개의 centroids를 갖는다. 임의의 데이터 포인트, $x_i$ 는 가장 가까운 centroid에 포함된다.

위와 같은 centroids는 아래와 같은 스텝을 반복하여 구해진다.

1. 현재 centroids의 위치를 기반으로 각 데이터 포인트, $x_i$를 각각의 클러스터에 할당한다.

2. 각각에 할당된 $x_i$들을 기반으로 centroids를 업데이트한다 (클러스터의 평균으로).

Fig. 1: K-Means Algorithm. 데이터 포인트는 점으로, centroids는 십자모양으로 표시됨. (a) 원래 데이터셋 (b) centroids를 임의로 초기화 (c-f) 주어진 centroids의 위치에 따라 각 포인트들이 cluster에 할당되고, 할당된 포인트를 바탕으로 centroids를 업데이트한다. k-means는 할당된 클러스터의 “평균”에 가까워지도록 centroids를 업데이트함.

각 클러스터들의 평균, 즉 centroids, $\{\mu_1, \mu_2, ..., \mu_k\}$ 는 초기에 initialize하고 학습 데이터, $\{x^{(1)}, ... , x^{(m)}\}$ 가 주어졌을 때 $k$개의 centroids와 각 데이터 포인트의 label, $c^{(i)}$ 를 구하는 것이 목표이다.

먼저 cluster centroids가 아래와 같이 initialize된다.

$$\mu_1, \mu_2, ..., \mu_k \in \R^n$$

$$\begin{align} c^{(i)} &:= \argmin_{j}|| x^{(i)} - \mu_j ||^2\\ \mu_j &:= \frac{\sum_{i=1}^{m}1(c^{(i)}=j)\cdot x^{(i)}}{\sum_{i=1}^{m}\mathcal{1}(c^{(i)}=j)} \end{align}$$

$1(i=j)$ 는 $i=j$ 라면 $1,$ 그렇지 않으면, $0$ 을 식으로 나타낸 것이다. 간단히 말해서 $(2)$ 식은 앞서 말한 바와 같이 클러스터에 할당된 데이터 포인트들의 평균이다.

$Eq. (1)$ 에서는 주어진 centroids를 바탕으로 각 데이터 포인트들의 label을 계산한다. $Eq. (2)$ 에서는 각 데이터 포인트들에게 할당된 label을 바탕으로 같은 label을 갖는 데이터 포인트들의 평균을 구하여 centroids를 업데이트한다.

본 과제에서 주어지는 코드는 아무것도 수정하지 않아도 바로 수행된다. 초기 실행은 꽤나 느리다. 따라서 “어디가” 개선이 필요하며 “어떻게” 개선할지를 찾아내는게 본 과제의 주요 골자이다.

성능 향상의 힌트는 “isolating performance hotspot” 이다. 즉 cost가 큰 코드를 찾아 이들을 분리하고 병렬 처리 기법을 적용하여 성능을 향상 시킬 수 있다. 그렇다면 hotspot을 찾는 것이 우선된다. 이를 위해 각 코드들의 수행 시간을 먼저 분석해보자.

To Do

1. data.dat 파일을 다운 받아서 kmeans를 빌드 및 수행. (data.dat 파일은 스탠포드 내부에서 사용되는 리눅스 서버에 있다. 로컬 수행을 위한 데이터 생성 코드가 따로 있어 이를 수행하여 테스트에 사용될 data.dat을 생성함.)

2. python 환경을 셋팅하고 plot.py 를 수행하여 잘 클러스터링이 되었는지 확인.

   

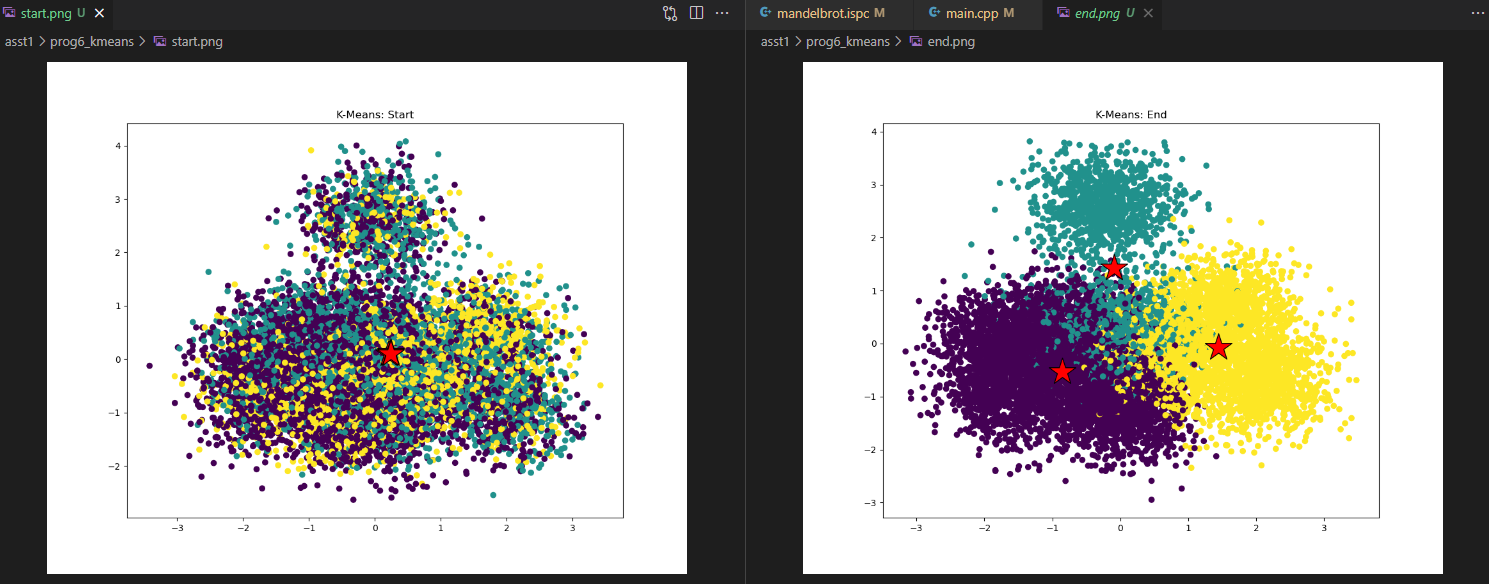
   Fig 2. 입력, 결과 plotting 예시 이미지

   위와 같이 나오면 된다.

3. common/CycleTimer.h 에 정의된 함수를 활용하여 코드 수행의 bottleneck을 찾는다.

4. 3. 에서의 관찰을 토대로 성능을 개선한다. 목표 개선은 $2.1\times$ 이상이다.

Contstraints & tips

kmeansThred.cpp 의 코드를 수정하는 것만으로 충분할 수 있음. kmenas 알고리즘 수행을 위한 로직을 수행하지 않는다.

💡

dist, computeAssingment, computeCentroids, computeCost 등의 함수 중 “하나”만을 병렬 처리 하여 통해 성능을 개선한다.

20-25 줄의 코드 수정 및 추가로도 충분히 해결가능함. 본 과제는 performance oriented programs을 profile하고 debug하는 스킬을 향상시키는데 중점을 둠. 이점을 고려하여 과제를 수행한다.

수행

1, 2번 수행

먼저 데이터를 생성하고 kmeans를 컴파일하고 수행하였다. 17초 정도의 수행시간을 보인다.

Fig 3. 원본 코드 수행 시간 (성능 향상의 기준이 되는 시간)

다음으로 plot.py 를 수행하여 제대로 클러스터링이 되는지 확인함. (잘됨)

Fig 4. 원본 코드를 수행하여 얻은 입력, 결과 plotting 이미지

3, 4번 수행

코드 분석

먼저 main 함수는 크게 3가지 정도의 파트로 나눌 수 있다.

1. 데이터 읽기 혹은 데이터 생성

   스탠포드 자체 서버에서 제공하는 데이터를 그대로 사용하는 경우가 데이터를 읽는 경우이고, 로컬에서 수행하는 경우를 위해 자체적으로 데이터를 생성하는 로직을 제공하였다.

2. KMeans 수행

3. 결과를 log파일의 형식으로 저장하여 결과를 python으로 plotting 할 수 있게함.

출제자의 의도를 파악한다면 응당 2. 의 시간이 가장 오래걸리고 우리의 optimization의 타겟이 되는 부분일 것이다. 2. 를 수행하는 함수는 kmeansThread.cpp의 아래 함수이다.

void kMeansThread(double *data, double *clusterCentroids, 
												int *clusterAssignments, int M, int N, int K, 
												double epsilon)

$M, N, K$는 각각 데이터의 갯수, 데이터의 차원수, cluster의 갯수이다. 앞선 식에서 $data$는 $\{x^{(i)}\}_{i=1}^M$ 들을 나타낸 것이며, $clusterCentroids$는 $\mu_1, \mu_2, ..., \mu_K$ 를 의미한다. $clusterAssignment$는 현재 centroids에 대한 각 데이터의 label이며, $c^{(i)}$ 에 해당하며, 각 data마다 대응된다.

kMeansThread에서 centroids를 계산하는 메인 로직은 아래와 같다.

/* Main K-Means Algorithm Loop */
  int iter = 0;
  while (!stoppingConditionMet(prevCost, currCost, epsilon, K)) {
    // Update cost arrays (for checking convergence criteria)
    for (int k = 0; k < K; k++) {
      prevCost[k] = currCost[k];
    }

    computeAssignments(&args);
    computeCentroids(&args);  
    computeCost(&args);       

    iter++;
  }

먼저 4개의 부분을 볼 수 있는데 stoppingConditionMet 은 cost를 기반으로 수렴여부를 판단하여 아래 while문을 더 수행할지 안할지를 결정한다.

computeAssignment는 주어진 centroids와 각 데이터 포인트들의 L2 distance를 계산하여 $K$개의 centroids 중 최소값의 distance를 갖는 centroids의 cluster에 “할당”된다. 각 데이터의 cluster, 즉 label 값은 clusterAssignments에 저장된다.

computeCentroids 에서는 앞서 각 cluster에 소속된 데이터들의 평균 (e.g. label 이 동일한 데이터들만의 평균) 을 구하고 이를 새로운 centroids로 “업데이트”한다.

computeCost 에서는 수렴 여부를 결정할 cost를 계산한다.

앞서 tips로 주어진 힌트인, dist, computeAssingment, computeCentroids, computeCost 등의 함수만을 병렬 처리를 통해 성능을 개선한다. 에서 힌트를 얻어 먼저 kmeansThread.cpp 코드 안에 있는 해당 함수들의 수행 시간을 측정한다.

dist 함수는 입력으로 주어진 두 개의 벡터간의 거리를 계산하는 것인데 이를 병렬 처리 하기 위해 thread를 생성하는 것은 큰 오버헤드라 판단되어 compute* 의 이름을 갖는 함수들만 성능을 측정한다. (다만, ISPC를 사용하면 쉽게 dist 함수 또한 parallelize 할 수 있을 것으로 판단됨.)

Fig 5. compute* 함수들의 각 수행시간

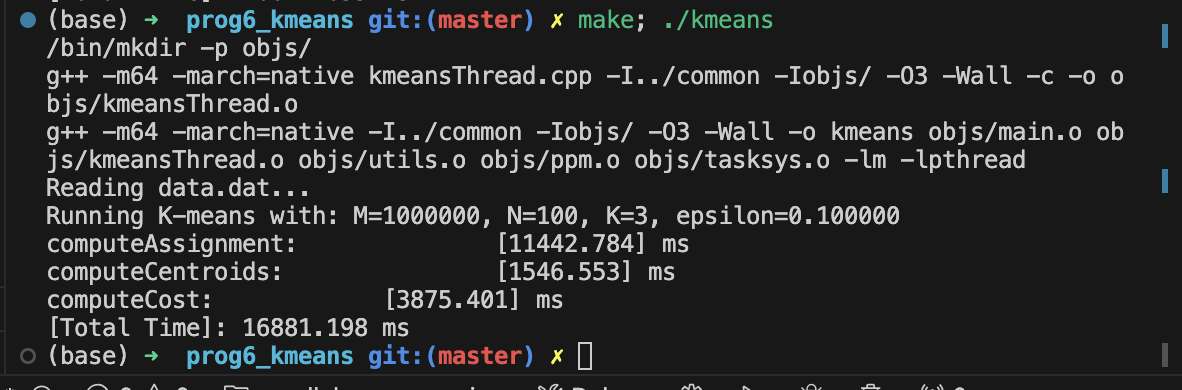
computeAssignment 의 수행시간이 다른 함수의 수행시간보다 3-7배 정도 많이 소요된다. 따라서 이 함수를 병렬화한다. 이를 위해 해당 함수의 코드를 병렬화가 가능하도록 independent한 부분과 그렇지 않은 부분으로 나눠야한다.

void computeAssignments(WorkerArgs *const args) {
  double *minDist = new double[args->M];
  
  // Initialize arrays
  for (int m =0; m < args->M; m++) {
    minDist[m] = 1e30;
    args->clusterAssignments[m] = -1;
  }

  // Assign datapoints to closest centroids
  for (int k = args->start; k < args->end; k++) {
    for (int m = 0; m < args->M; m++) {
      double d = dist(&args->data[m * args->N],
                      &args->clusterCentroids[k * args->N], args->N);
      if (d < minDist[m]) {
        minDist[m] = d;
        args->clusterAssignments[m] = k;
      }
    }
  }

  free(minDist);
}

위 코드는 두 부분으로 나누어 볼 수 있다. 먼저, $M$개의 데이터가 각각 사용할 최솟값을 저장할 메모리를 할당한다. 다음은 $m$번째 데이터와 $k$ 번째 centroids 간의 거리를 계산하여 만약 최소값이라면, 최소값을 업데이트하고 최소값이 갱신됐을 때, $m$번째 데이터는 해당 $k$에 속한다고 assign을 해준다.

노랗게 하이라이트된 부분이 바로 우리가 찾는 independent한, 즉, SPMD가 가능한 부분이다. $M$개의 데이터들을 $M / T$ (where, $T$ = # of threads) 개의 데이터로 나누어 thread 별로 이들을 처리하도록 한다. 따라서 각각의 threads에 해당 부분을 함수 포인터로 주기 위해 이 부분을 따로 떼어내어 assignCluster 라는 함수로 선언한다.

void assignCluster(WorkerArgs *const args) {
  for (int m=args->start; m<args->end; m++) {
      double d = dist(&args->data[m * args->N],
                      &args->clusterCentroids[args->k * args->N], args->N);
      if (d < args->minDist[m]) {
        args->minDist[m] = d;
        args->clusterAssignments[m] = args->k;
      }
    }
}

따라서 args에 있는 멤버 변수들 중 start, end 를 사용하여 각 thread가 담당할 데이터의 구역을 나눈다. 여기엔 특별한 주의가 필요한데 $k$와 최솟값들을 저장하는 배열의 포인터, $minDist$ 를 추가적으로 알려줘야하기 때문에 아래와 같이 WorkerArgs struct에 $k, minDist$를 추가한다.

typedef struct {
  // Control work assignments
  int start, end;
  int k;
  double *minDist;

  // Shared by all functions
  double *data;
  double *clusterCentroids;
  int *clusterAssignments;
  double *currCost;
  int M, N, K;
} WorkerArgs;

그리고 마지막으로 computeAssignment 함수도 아래와 같이 작성한다.

void computeAssignments(WorkerArgs *const args) {
  int start, end;
  double *minDist = new double[args->M];
  int numThreads = 32;

  // Initialize arrays
  for (int m=0; m < args->M; m++) {
    minDist[m] = 1e30;
    args->clusterAssignments[m] = -1;
  }

  std::thread workers[numThreads];
  WorkerArgs thread_args[numThreads];
  for(int i=0; i<numThreads; ++i) {
    thread_args[i].data               = args->data;
    thread_args[i].clusterCentroids   = args->clusterCentroids;
    thread_args[i].clusterAssignments = args->clusterAssignments;
    thread_args[i].currCost           = args->currCost;
    thread_args[i].M                  = args->M;
    thread_args[i].N                  = args->N;
    thread_args[i].K                  = args->K;
  }

  // Assign datapoints to closest centroids
  for (int k=0; k<args->K; k++) {
    for(int i=0; i<numThreads; ++i) { 
      start = i * (args->M / numThreads);
      end = (i + 1) * (args->M / numThreads);
      if (i == numThreads-1) {
        // For in case that M % numThread != 0
        end = args->M;
      }

      thread_args[i].start = start;
      thread_args[i].end = end;
      thread_args[i].k = k;
      thread_args[i].minDist = minDist;

      // Serial version
      // assignCluster(&thread_args[i]);
    }

    // /* Thread version 
    for(int i=1; i<numThreads; ++i) {
      workers[i] = std::thread(assignCluster, &thread_args[i]);
    }
    assignCluster(&thread_args[0]);
    for(int i=1; i<numThreads; ++i) {
      workers[i].join();
    }
    // */
  }

  free(minDist);
}

먼저 num_threads를 32로 선언했다 (32개의 코어를 가진 서버에서 수행하였기 때문). 그리고 이 숫자에 맞춰 std:thread와 각 thread별로 할당할 thread_args를 선언한다. 동일한 값을 갖는 args의 값들을 미리 복사해둔다. 데이터를 나눌 start, end 변수를 적절히 계산하여 구해주고 이를 각 thread_args의 control variables에 할당한다. thread를 첫 번째를 제외 ($\because$ 메인 프로세스에서 수행) 하고 모두 thread를 생성하여 수행시킨다. 그리고 모든 thread가 끝나기를 기다렸다가 (synchronization) 수행을 마무리한다.

수행 결과는 다음과 같다.

Fig 6. 최종 수행 결과

computeAssignment 함수의 수행 시간이 11442ms → 1698ms 로 많이 줄어 들었고 최종적으로 수행 성능 향상, spped up은 $2.2\times$ 정도 향상 되었다. computeCentroids, computeCost에도 thread를 활용하여 성능 향상을 기대할 수 있고 dist 함수에 ISPC를 사용하면 computeAssignment, computeCost 함수의 실행 시간을 약 1/8 (보통 vectorized 연산의 width) 수준으로 더 줄일 수 있을 것으로 기대된다.

Uploaded by N2T