Deep Q-Learning

Introduction of Deep Q-Learning

• 이전 시간에 Q-Learning을 배웠고 FrozenLake-v1 ☃️ and Taxi-v3 🚕 에서 좋은 성능을 보였다.

• 간단한 알고리즘을 통해 훌륭한 결과를 얻었으나 이러한 enviroments는 사실 상대적으로 굉장히 심플한 편이다. 왜냐하면 state space가 discrete하고 작았기 때문이다. 예를 들어 Atari 게임의 경우 $10^9 - 10^{11}$ 개의 state를 가질 수 있다.

• 이러한 경우 Q-table을 사용하여 결과를 내고 이를 update하는 과정은 비효율적이다.

• 본 unit에서는 첫 Deep Reinforcement Learning Agent를 학습한다. 이를 Deep Q-Learning(이하 DQN)이라고 한다. Q-table을 사용하는 대신 DQN은 state를 입력으로 받고 주어진 state에 기반한 action들에 대한 Q-values를 추정(approximate)하는 Neural Network를 사용한다.

• RL-Zoo Space invaders와 다른 Atari 게임들에 대하여 학습 시킬 예정이다.

Deep Q-Network (DQN)

• Q-Learning은 Q-Function, 즉 어떤 state, 어떤 행동을 취할지에 대한 value를 측정하는 action-value function을 학습시키는 알고리즘이다.

• 문제는 이러한 Q-Learning 방식은 Tabular Method라는 점이다. 이러한 방식은 array나 table에 효과적으로 표현할만큼 state와 action의 space가 작지 않을 때 문제가 된다.
  • 다른 말로 Not Scalable 하다고 한다.

• 하지만 우리가 오늘날 하는 것을 생각해보면 화면(frame)을 input 으로 받는 Space Invader나 다른 더 복잡한 게임을 하도록 agent를 학습한다. Atari 게임은 frame을 input으로 받는다. atari 게임의 frame은 (210, 160, 3)의 dimension을 갖는다. 그리고 각 0부터 255 사이의 값을 가질 수 있으므로 frame의 서로 다른 state의 총 갯수는 아래와 같다.
  • $255^{210*160*3} = 255^{100800}$

  우주의 원자의 수가 $10^{80}$ 개 정도로 알려져있으니 우주의 원자수보다 아득히 많은 state의 갯수이다.

  

• 따라서 state space가 아주아주 크다. 이러한 이유로 Q-table을 생성하고 update하는 것은 효율적이지 않다. 이러한 경우, best 아이디어는 parameterized Q-function $Q_\theta(s, a)$ 를 사용하여 Q-values를 추정(approximation) 하는 것이다.

• 이렇게 학습된 Neural Network는 주어진 state에서 가능한 모든 action들의 서로 다른 Q-values를 추정한다.

• DQN을 아래와 같이 정의할 수 있다.

  

• input으로 4개의 frame을 stack하여 이를 state로 network에게 준다. 그리고 주어진 state에서의 가능한 action들의 Q-values의 vector를 output으로 낸다.

• DQN의 성능이 처음엔 안좋겠지만 학습을 진행하며 점점 좋아진다.

Preprocessing the input and temporal limitation

• input preprocessing은 state의 complexity와 학습에 필요한 computation time을 줄이기 위해 필수적이다.

• state space를 84x84로 줄이고 이를 grayscale로 변환하여 사용한다. Atari game에서 색상 정보는 보통 중요하지 않기 때문이다. 또한 210x160 의 크기에서 플레이에 필요한 84x84 의 사이즈만으로 crop 및 resize를 진행한다.

• frame을 4개의 stack으로 쌓는 이유는 Temporal Limitation을 다루기 위해서다
  • Temporal Limitation: 한 장의 frame으로는 시간적인 정보를 담지 못한다.

    

  • 하지만 여러 장의 연속된 frame은 시간적인 정보를 어느 정도 유지한다.

    

• 한 장의 frame으로는 공이 어느 방향으로 이동하는지 알 수 없지만 3장의 frame으로는 공이 어느 방향(오른쪽)으로 진행하는지 알 수 있다.

The Deep Q-Learning Algorithm

• Q-Learning과 DQN의 차이는 다음과 같다.
  • Q-Learning은 Q-table에서 state-action pair의 Q-value를 직접적으로 update한다.

    

  • DQN은 추정(approximate)한 Q-Value와 Q-Target 의 비교한 Loss Function을 가지고 Gradient Descent의 방법으로 DQN의 weight를 update한다.

    

• Deep Q-Learning training algorithm에는 두 개의 phase가 있다.
  1. Sampling: Action을 취하고 observed experience tuples를 replay memory에 저장한다.
  2. Training: 앞서 sampling한 tuples의 일부를 random하게 뽑은 batch를 이용해 GD로 weight를 update한다.

  

Training Instability

• DQN은 여러 layer의 non-linear function의 조합으로 이루어져 있으며 loss function을 bootstraping으로 계산하기 때문에 학습이 불안정하다.

• 따라서 학습을 안정화(stabilize) 하기 위해 아래 3가지의 solution을 따를 수 있다.
  1. Experience Replay
     • experiences를 더욱 효율적으로 사용
  2. Fixed Q-Target
     • 학습 안정화
  3. Double Deep Q-Learning
     • Q-Value의 overestimation problem 해결

Experience Replay

• DQN에서의 Experience Replay는 아래와 같은 2개의 function을 갖는다.
  1. 학습 시 experiences를 더욱 효율적으로 사용하게 한다.
     • 보통 online RL에서는 agent가 environment와 interact하고, experience(state, action, reward, next state)를 받고, 이를 통해 학습하고 해당 experience를 버린다(discard). 이는 효율적이지 못하다.
     • 학습 중 재사용이 가능하도록 experience samples를 replay buffer에 저장한다.

     

     → 이를 통해 agent는 같은 experience로부터 여러번 학습이 가능하다.

  2. previous experience를 잊는 것(forgetting)을 피하고 experience간의 correlation을 줄인다.
     • 만약 Neural Network에 sequential experience를 주었을 때에 우리에게 생길 문제는 새로운 experience를 받으면 이전 experience는 잊어버린다는 것이다.
     • Solution은 environment와 interact하면서 얻은 experience tuples를 저장할 Replay Buffer를 생성하고 여기서 작은 tuples의 batch를 sampling하는 것이다. 본 solution을 통해 network가 방금 전에 얻은 experience만으로 학습하는 것을 방지할 수 있다.
     • Experience Replay는 다른 이점도 있다. Experiences를 randomly sampling 함으로써 observation sequences 간의 correlation을 제거할 수 있고, action-value가 oscillating 하거나 극단적으로 발산하는 경우를 피할 수 있다.

• DQN pseudo code에서 Replay Buffer $D$ 를 $N$의 capacity로 initialize하는 것을 볼 수 있다. 그리고 experiences를 buffer에 저장하고 이를 batch로 sampling하여 DQN의 training phase에서 사용하는 것을 알 수 있다.

  

Fixed Q-Target

• TD error, (a.k.a Loss)를 계산할 때, 우리는 TD Target과 추정된(estimated) Q-value 의 차이를 계산한다. 하지만 학습 초기에는 제대로 된 TD target을 알 길이 없기 때문에 이를 말 그대로 추정 해야한다.

• TD target은 현재 취한 action에 대한 reward와 다음 state에서의 가장 큰 Q Value를 discounted 한 값을 더한 것이다.
  • $R_{t+1} + \gamma*max_aQ(S_{t+1}, a)$ ← TD Target

  하지만 문제는 추정된 TD Target 자체도 결국에는 아직 학습이 덜 된 학습중인 같은 모델에 의해서 추정된 값이므로 TD target과 학습하고자 하는 parameters에 아주 큰 상관관계가 존재한다.

• 따라서 매 step마다 parameters를 update한다면 parameters에 의해 추정된 Q Value 뿐만 아니라 TD Target도 같이 움직이게(shifted) 된다. 이는 moving target을 쫓는 것과 마찬가지다. 이런 방식으로 학습을 하게 된다면 학습이 크게 oscillation 한다.

• 마치 cowboy가 cow를 쫓는 것과 같다.

  

  

  

  

  oscillation 한다.

• 따라서 아래와 같은 전략을 취한다.
  1. TD Target을 추정하기 위 Network를 따로 분리하여 parameters를 고정해놓고 사용한다.
  2. DQN의 parameters를 매 C step마다 copy하여 target network를 update 한다.

  

Double DQN

• Double DQNs, Double Deep Q-Learning Neural Network라고 불리는 이것은 Hado Van Hasselt에 의해 소개됐다. 이 방법은 Q-Values의 overestimation problem을 다루기 위해 제안됐다.

• Q-Value overestimation problem을 이해하기 위해 TD Target이 어떻게 계산되는지 다시 살펴보자

  

💡

next state에서의 가장 높은 Q-Value를 가진 action이 어떻게 최선의 action인지 확신할 수 있는가?

• 앞서 공부한바와 같이 좋은 Q-Value estimation은 시도해봤던 action과 next state의 주변 state들로 인해 결정된다.

• 결과적으로, 학습의 초기단계에서 취해야할 최선의 action에 대한 정보를 우리는 알지 못한다. 따라서 단순히 가장 큰 Q-Value를 갖는 action을 다음 행동으로 취한다면 false positive case가 많아 질것이다. 또한 optimal하게 학습되지 못한 value function이 계속해서 optimal best action이 아닌 다른 action에 가장 높은 Q-Value를 준다면 학습이 굉장히 복잡해질 것이다.

• solution은 다음과 같다.
  • Q target을 계산할 때, 두 개의 network를 사용하는 것이다.
    1. DQN Network: To select the best action for the next state
    2. Target Network: next state에서 앞서 선택한 action을 취했을 때의 target Q-value를 계산하는 Network

• 위와 같은 방법으로 DDQN은 Q-Value를 overestimate하는 것을 줄일 수 있고, 결과적으로 안정적인 학습과 학습 시간 감소의 효과를 기대할 수 있다.

Double DQN (DDQN)

Double Deep Q Networks

Tackling maximization bias in Deep Q-learning

https://towardsdatascience.com/double-deep-q-networks-905dd8325412

https://arxiv.org/pdf/1509.06461.pdf

Overestimation

Motivation

• Target Q-Value 를 살펴보자

  

  여기서도 특별히

  

  max값을 취하는 것은 그 순간의 max값을 갖는 action이 최선이다라고 “추정”을 하는 것이다.

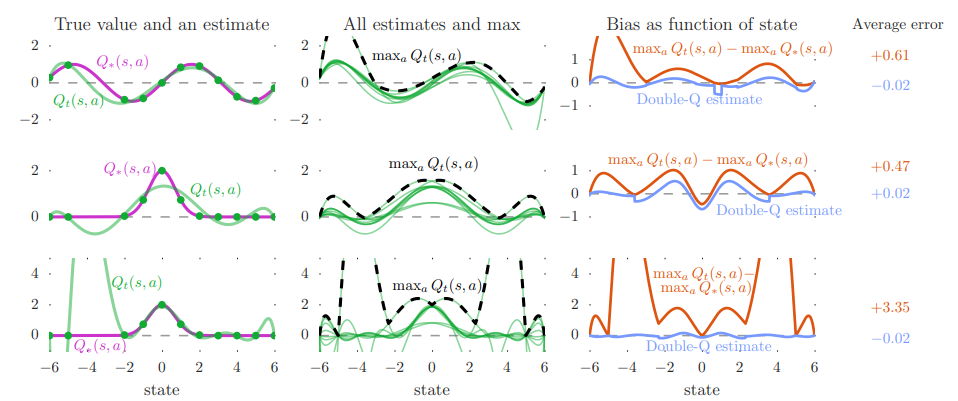
• 예를 들어 어떤 state $S$ 가 주어졌을 때 optimal한 Q-Value값은 모두 사실 0 이었다고 하자. 하지만 어떠한 action $A_1$하나의 Q-Value가 0.01, 나머지는 모두 -0.01 이었다고 가정했을 때 실상은 $A_1$의 Q-Value는 0이지만 운이 좋게도 최선의 선택이 되버린 것이다.

• Hasselt et al. 논문에서는 이러한 overestimation bias를 여러가지 Atari game을 통해 실험하였다.

  

  

  • 결과에서 볼 수 있듯이, simple DQN은 action-value를 overestimate하는 경향이 있으며, 학습이 unstable하다.

Solution: Double Q-Learning

• solution은 서로가 서로를 update하기 위해 사용되도록 Q-value estimators를 두개로 분리하여 사용하는 것이다.

• 이렇게 서로 독립적인 estimators를 사용하면 서로가 서로의 estimator가 선택선 action의 Q-value 추정치의 편향을 줄일 수 있다.

Uploaded by N2T