Policy-Gradient

Introduction

지난 유닛에서 우리는 Deep Q-Learning을 배웠다. 이러한 Value-Based Deep RL 알고리즘에서 우리는 Deep Neural Network를 사용하여 서로 다른 Q-Value 들을 주어진 state에서 취할 수 있는 action들을 예측하였다.

코스의 시작부터 우리는 value-based method, optimal policy를 찾는 중간 과정으로써 value function을 예측하는 방법만을 공부하였다.

value-based method에서 policy $\pi$ 는 단지 action-value를 추정하기 위해서만 존재한다. 이는 policy가 단지 주어진 state에서의 가장 높은 value를 갖는 action을 선택하는 함수이기 때문이다.

Policy-Based Methods에서는 value function을 학습하는 중간 과정 없이 policy를 “직접” 학습하길 원한다.

그래서 이번 챕터에서는 policy-based method에 대하여 공부할거고 이 method의 subset인 Policy-Gradient에 대해서 공부한다. 그리고 첫 번째 Policy-Gradient Algorithm인 Monte Carlo Reinforce를 Pytorch로 from scratch로 구현한다. 그런 다음 CartPole-v1과 PixelCopter Environments에서 본 method의 robustness를 테스트한다.

What are the Policy-Based Methods?

RL의 메인 목표 중 하나는 optimal policy $\pi^*$, expected cumulative reward를 최대화 하는 policy를 찾는 것이다. 이는 reward hypothesis에 근거한다.

• reward hypothesis:

  모든 목표(goals)는 expected cumulative reward를 최대화하는 것으로 표현할 수 있다.

예를 들어 축구에서의 목표는 게임에 이기는 것이다. RL의 관점에서 이를 표현하면 상대방의 골대 안에 골을 최대한 많이 넣는 것으로 표현할 수 있다. 그리고 우리 측 골대에 공이 들어가는 것을 최소화하는 것이다.

Value-Based, Policy-Based, Actor-Critic Methods

첫 번쨰 유닛에서 우리는 optimal policy $\pi^*$ 를 찾는(대부분 추정하는 것이었지만) 두 가지 methods 를 보았다.

• Value-Based [Value Function]
  • optimal value function이 optimal policy로 이어진다는 아이디어
  • true action-value function에 근사하도록 value function의 target value와 예측된 value 값 사이의 loss를 최소화하는 것이 목표.
  • policy가 있지만 이는 암시적임. 왜냐하면 value function으로 부터 값을 그대로 사용하기 때문임.

• Policy-Based
  • Policy 자체를 parameterize 하는 것이 아이디어. 예를 들어 neural network $\pi_\theta$ 를 사용한다면, policy는 actions이 주어졌을 때의 확률 분포(probability distribution over actions)를 결과로 낼 것이다. [Stochastic Policy]

    

  • 목표는 그래서 gradient ascent를 사용하여 parameterized policy의 성능을 최대화 하는 것이다.

    

  • 다음으로 Actor-Critic Method, value-based, policy-baesd 방법을 섞은 method를 공부한다.

결과적으로 policy-baesd method 덕분에 policy $\pi_\theta$ 를 직접 학습하여 best cumulative return으로 lead하는 probability distribution over actions $\pi_\theta (a|s)$ 를 얻을 수 있다. 이를 위해 objective function $J(\theta)$ 를 정의한다. 즉, expected cumulative reward. 그리고 objective function을 최대화하는 value $\theta$ 를 찾는다.

The difference between Policy-Based and Policy-Gradient Methopds

먼저 Policy-Gradient Method는 Policy-Based Method의 하위 카테고리이다. Policy-Based Method에서 optimization은 대부분 on-policy 로 진행된다. 왜냐하면 매 업데이트마다 가장 최근의 버전인 $\pi_\theta$ 로 부터 생성된 데이터만을 사용하기 때문이다.

두 Methods의 차이는 parameter $\theta$를 어떻게 optimize 하느냐에 달려있다.

• Policy-Based Method는 optimal policy를 직접적으로(directly) 찾는다. 하지만 parameter $\theta$는 hill climbing, simulated annealing 혹은 evolution strategies 등으로 간접적으로(indirectly) 찾는다.

• Policy-Gradient Methods는 이 역시 Poliby-Based method의 아래에 있기 때문에 optimal policy를 직접적으로 찾는다. 그리고 paramter $\theta$ 는 objective function $J(\theta)$ 의 성능에 따른 Gradient-Ascent 방법으로 직접 찾는다.

💡

Q-Learning도 잘하는데요 왜 Policy-Gradient를 쓰나요?

Advantages

• The Simplicity of Integration
  • value estimation 과정이 줄어들어 중간 과정이 생략됐다. 따라서 더욱 심플함.

• Policy-Gradient Methods can learn a stochastic policy
  • Policy-Gradient Methods는 value function은 그러지 못했던 stochastic Policy를 학습할 수 있다. 이는 두 가지 결과를 낳는다.
    1. exploration/exploitation trade-off 를 직접 다룰 필요가 없어진다. 이는 취할 수 있는 action들을 확률분포로 알려주어 agent가 항상 같은 전략(trajectory)를 취하지 않을 수 있기 때문이다. (sampling하면 아무리 10%의 action이더라도 취할 수도 있음)
    2. perceptual aliasing 문제를 피할 수 있다. perceptual aliasing은 두 state가 보기에는 같지만 서로 다른 action을 취해야하는 경우를 말한다.

       

       예시를 들면, 로봇 청소기는 먼지를 청소해야하고 햄스터를 피해야한다. 여기서 두 빨강 타일은 aliased 된 state이다. 왜냐하면 각 state를 번호로 구분하는 것이 아닌 주변의 벽만을 본다면 이 둘은 정확히 같은 state로 볼 수 있기 때문이다.

       

       따라서 deterministic 하게 이동하면 빨강 타일에서 항상 왼쪽 혹은 오른쪽으로만 이동하게 되어서 위와 같이 어느 한 방향에 걸려버리는(stuck) 상황이 발생할 수 있다.

       

       반면, optimal stochastic policy에서는 빨강 타일에서 왼쪽, 오른쪽을 random하게 이동할 것이다. 따라서 걸리지 않고 높은 확률로 목표를 달성할 수 있을 것이다.

• Policy-Gradient Methods는 action-space가 큰 경우(high-dimensional) 와 continuous action space를 갖는 경우에 더욱 효과적이다.

  Deep Q-Learning의 문제는 모든 가능한 action에 대하여 점수(score)를 예측한다는 점이다. 그러나 만약 취할 수 있는 actions이 무한하다면..?

  예를 들어 자율 주행의 경우 각 state 마다 취할 수 있는 action이 무한하다 (e.g. 휠을 15도, 17.2도 틀어라 등등). Q-Learning을 사용한다면 이러한 action에 모두 Q-Value값을 구하여야한다. continuous output으로 부터 max의 action을 찾는 것 자체가 optimization problem이다.

  대신, Policy-Gradient Method로 action에 따른 확률 분포(Probability Distribution over actions) 를 output으로 가질 수 있다.

• Policy-Gradient Methods 는 더 잘 수렴하는 특징이 있다.

  Value-Based Methods에서는 value function을 update하기 위해 공격적인 연산자를 사용하였다. : $max(Q_{estimation})$

  결과적으로 추정된(estimated) Q-estimated에 임의의 작은 변화가 주어지면, 그리고 그 어떤 action의 Q-estimated가 maximal이 된다면 action probability 가 극적으로 변하게 된다.

  예를 들어 만약 왼쪽으로 이동하는 것이 best 였을 때 ($Q_{left}=0.22$), 다음 step을 학습을 하였더니 $Q_{right} = 0.23$ 이 돼 버린다면 앞으로 policy는 거의 항상 오른쪽을 택할 것이기 때문에 기존에 왼쪽을 선택하던 trajectory를 급격하게 바꾼 셈이 된다.

  반면 Policy-Gradient 방식, 즉 stochatstic policy action preference는 시간에 따라 smooth하게 변한다.

Disadvantages

당연히 Policy-Gradient Method도 단점이 있다.

• Policy-Gradient Method는 Global Maxima보다 Local Maxima 에 빠지는 경우가 많다.

• 학습이 오래 걸린다.

• high variance를 갖는다. 이는 Actor-Critic Section에서 왜 그런지, 또 어떻게 해결하는지 공부한다.

Getting the big picture

방금 전 우리는 expected return을 최대화 하는 parameters $\theta$를 찾는 것에 초점을 맞춘 Policy-Gradient Methods를 공부하였다.

아이디어는 parameterized stochastic policy가 있고, 이 경우에 probability distribution over actions가 output으로 주어진다. 이렇게 취할 action에 대한 probability를 action preference 라고도 한다.

예제로 CartPole-v1 을 활용한다.

• Input: state

• output: state가 주어졌을 때 각 action들에 대한 probability distribution.

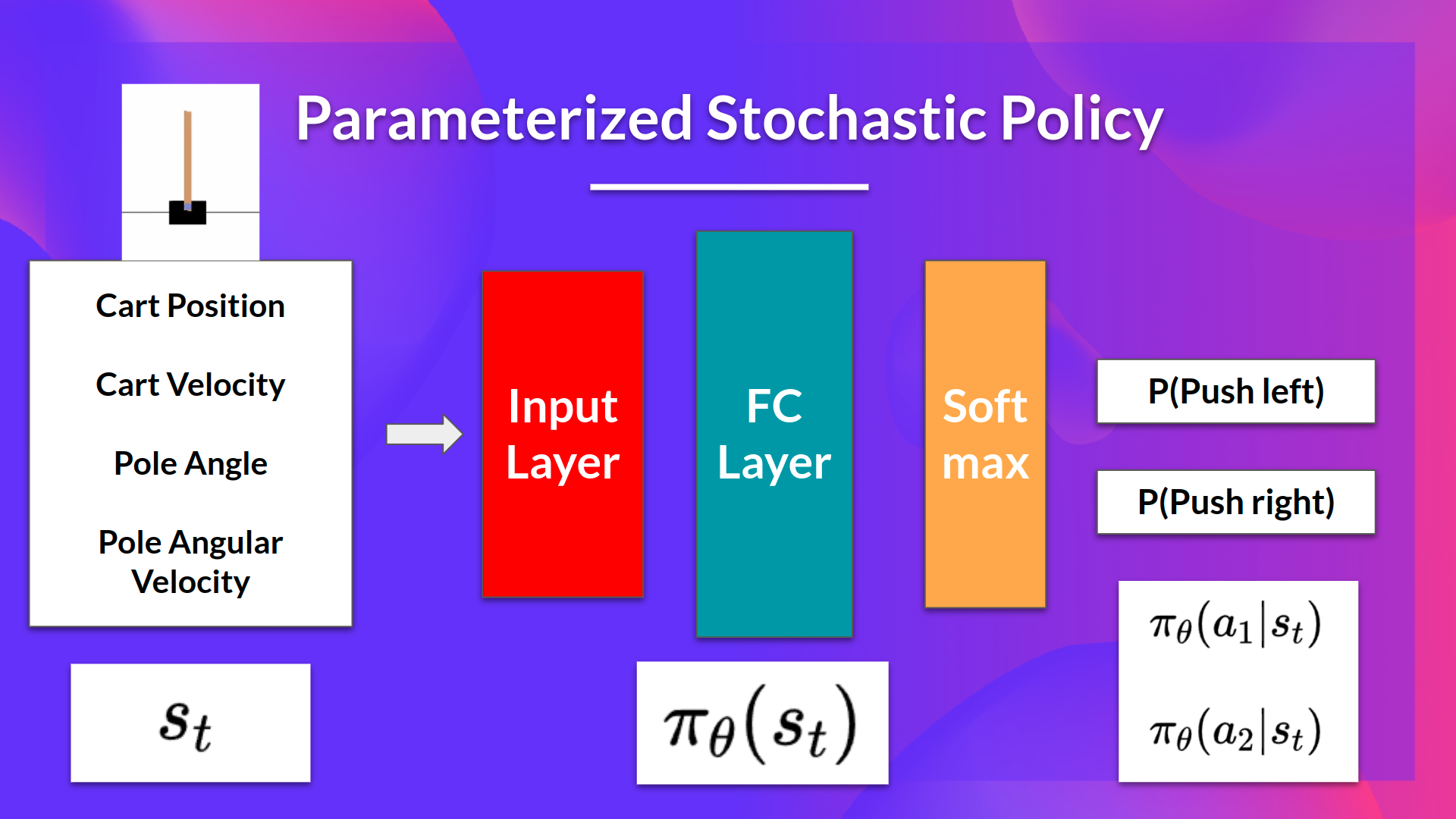
Policy-Gradient 와 함께 하는 우리의 목표는 미래에 더 나은 action을 선택하도록 policy를 튜닝하여 probability distribution over actions를 잘 조절(control) 하는 것이다. agent가 Environment와 상호작용하는 매 시간마다 parameters를 쥐어짜서 더 나은 선택을 하도록 한다.

아이디어는 episode 중간에 agent가 상호작용하게 하는 것이다. 만약 episode에서 이기면 취했던 각 action이 좋았다고 판단하고 미래에 더 자주 sample되도록 한다.

따라서 각 state-action 쌍에 대하여 $P(a|s)$ 를 더욱 크게 하고 싶은 것이고, 만약 졌다면 감소시킨다.

위는 Policy-Gradient의 Psudo code이다.

Diving deeper into Policy-Gradient Methods

stochastic policy $\pi_\theta$ 가 주어졌고 parameters $\theta$ 를 갖는다.

$\pi_\theta (s_t|a_t)$ 는 state $s_t$가 주어졌을 때 action $a_t$를 선택할 확률이다.

The Objective Function

the objective function은 trajectory(reward를 고려하지 않은 state, action의 sequence)가 주어졌을 때의 agent의 performance를 알려준다. 그리고 output으로 expected cumulative reward를 갖는다.

The expected return (== expected cumulative reward)은 weighted average이다. (weights는 취할 수 있는 모든 return $R(\tau)$의 확률 $P(\tau; \theta$)로 주어진다.)

$R(\tau)$: 임의의 trajectory로 부터의 Return. 해당 값을 얻고 이를 이용해 expected return을 계산하려면 여기에 가능한 각 trajectory의 확률을 곱해야한다.

$P(\tau; \theta)$: .가능한 각 trajectory $\tau$의 확률. 이 확률은 $\theta$에 종속적이다. 왜냐하면 이 $\theta$가 policy를 결정하고 이 policy를 사용하여 방문한 states에 영향을 주는 trajectory의 actions을 선택하기 때문이다.

$J(\theta)$: Expected return. 모든 trajectory, 즉 $\theta$가 주어졌을 때 어떤 trajectory를 취할 확률과 그 trajectory의 return을 곱한 이들을 모두 더하여 구한다.

우리의 목표는 expected cumulative reward를 최대화 하여 parameters $\theta$ 가 최선의 확률 분포를 output으로 갖도록 하는 것이다.

Gradient Ascent and the Policy-Gradient Theorem

Policy-Gradient 는 optimization problem이다. 여기서 objective function $J(\theta)$ 를 최대화하는 $\theta$ 의 값을 찾고자 한다. 따라서 Gradient-Ascent를 사용한다. 이는 Gradient-Descent의 반대(inverse)이다.

하지만 $J(\theta)$의 derivative를 계산하는데에 두 가지 문제점이 있다.

1. objective function의 “true” gradient를 계산할 수 없다. 이를 계산하기 위해서는 가능한 모든 trajectory들의 확률값들이 필요한데 이는 아주아주아주 계산량이 많다. 따라서 sample-base estimate로 gradient의 estimation을 추정한다.

2. objective function을 미분하기 위해서는 Markov Decision Process dynamics라고 불리는 state distribution을 미분해야한다. 이는 Environment에 붙어있다. 문제는 우리는 Environment가 어떻게 생긴지 모르므로 이를 미분할 수 없다는 점이다.

다행히 Policy Gradient Theorem 이라는 solution을 사용하여 이 문제를 해결할 수 있다. 이는 state distribution을 미분하지 않아도 되도록 objective function을 미분 가능한 함수로 reformulate한다.

The Reinforce Algorithm (Monte Carlo Reinforce)

Reinforce Algorithm, Monte-Carlo Policy Gradient Algorithm 이라고도 불리는 이 알고리즘은 policy parameters $\theta$ 를 update 하기 위해 모든 episode로 부터의 추정된(estimated) return을 사용한다.

• policy $\pi_\theta$ 를 사용하여 episode $\tau$ 를 모은다.

• 앞서 구한 episode $\tau$를 활용하여 gradient $\hat{g} = \nabla_\theta J(\theta)$ 를 추정(estimate)한다.

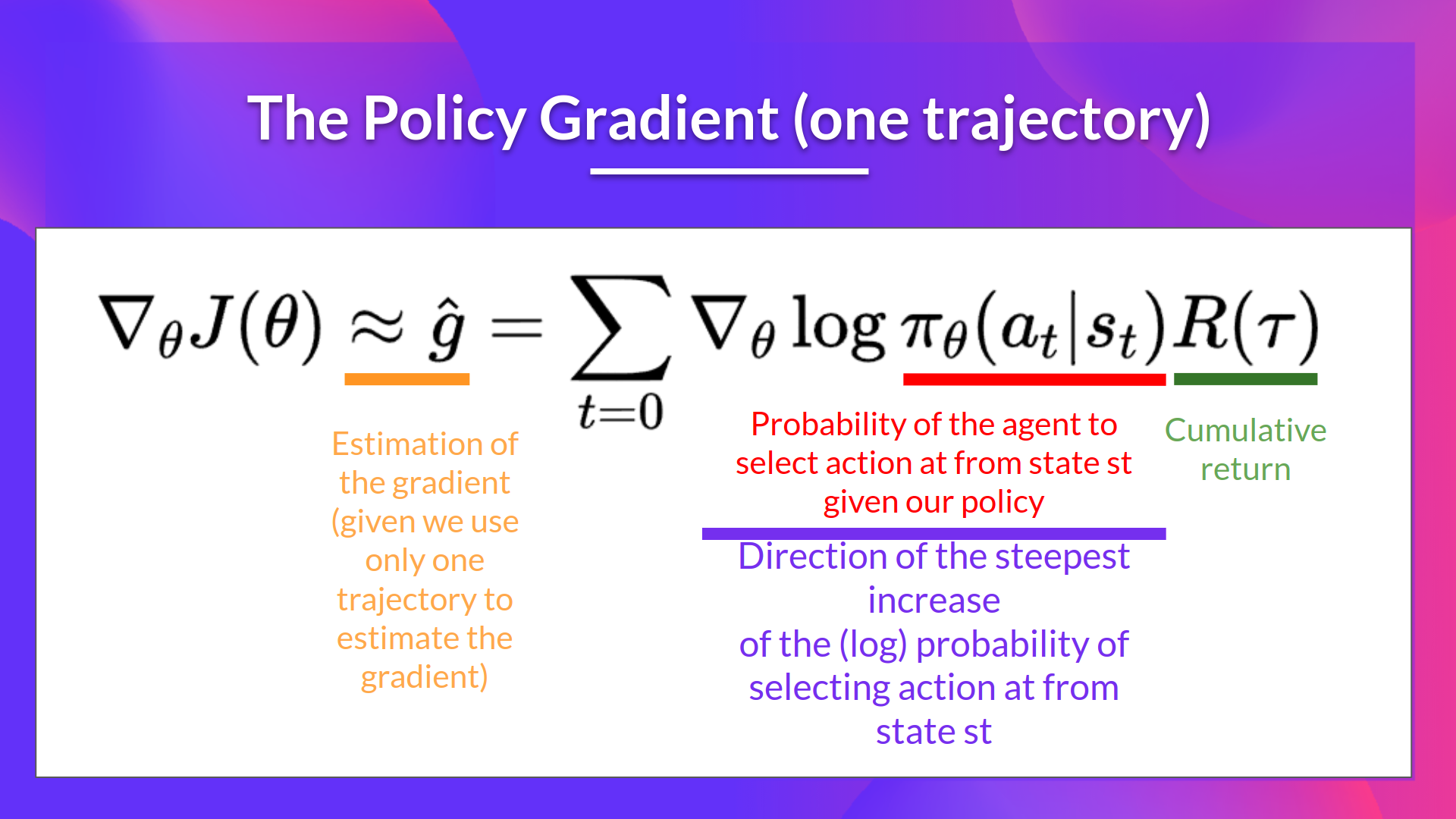
• update policy $\theta$: $\theta ← \theta + \alpha \hat{g}$

위 업데이트를 아래와 같이 해석할 수 있다.

• $\nabla_\theta log\pi_{\theta}(a_t | s_t)$ 는 state $s_t$로부터 가장 가파른, action을 선택하는 확률이 증가하는 방향이다. 이는 따라서 state $s_t$ 에서 action $a_t$를 선택할 확률을 증/감시킬 때 policy의 weights를 어떻게 바꿔야하는지에 대해 나타낸다.

• $R(\tau)$ : scoring function이다.
  • 만약 return 값이 높으면 (state, action)의 조합들의 확률값들을 높일 것이다.
  • 반면, return 값이 낮으면 조합의 확률값을 낮출 것이다.

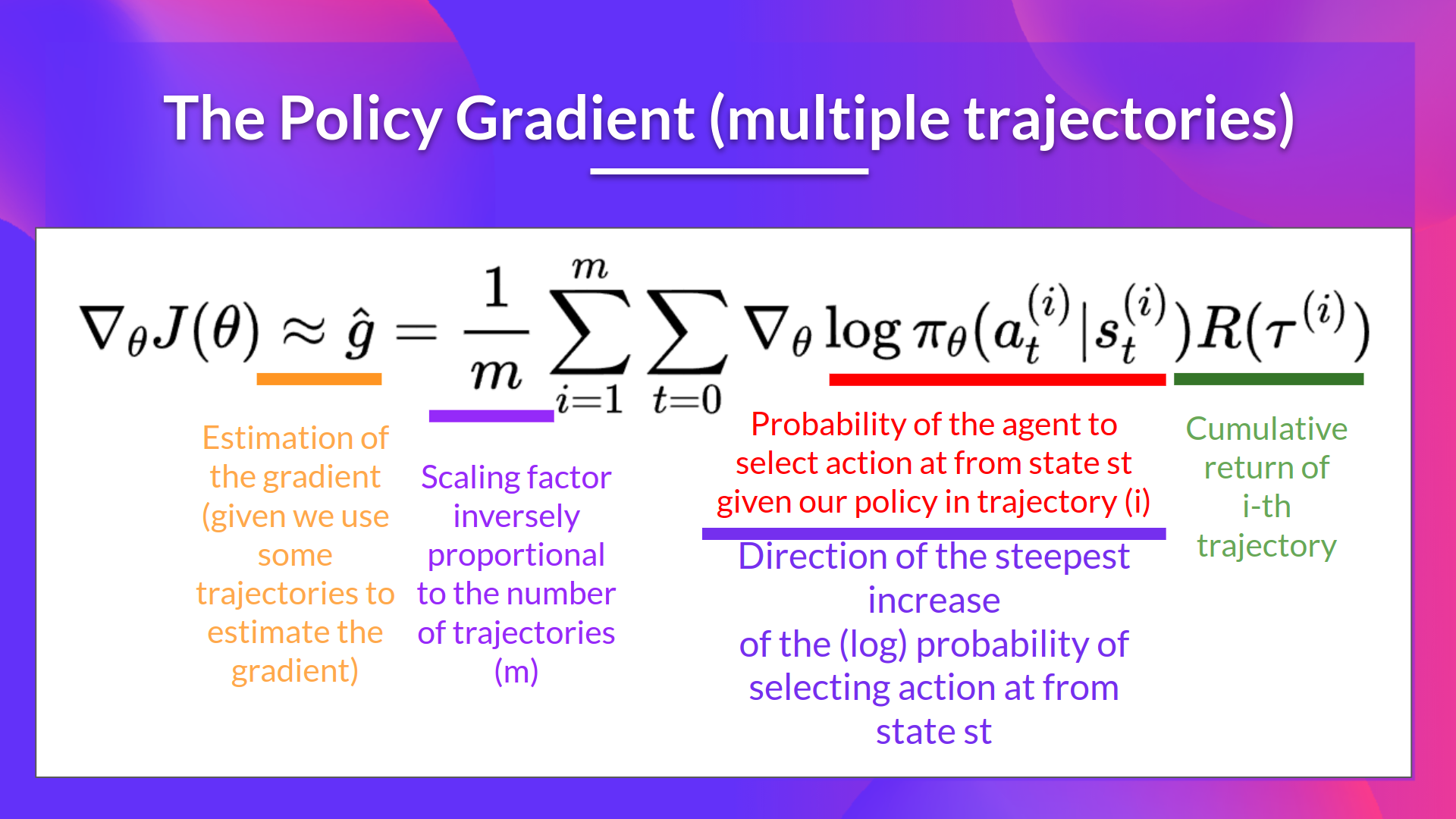
또한 gradient를 계산하기 위해 여러(multiple) episodes를 사용할 수 있다.

Uploaded by N2T