Q-Learning

Two Types of Value-Based Methods

• Value-Based Methods에서는 state가 주어졌을 때 어떤 state로부터 expected value를 학습한다.

• 어떤 state의 value는 그 state로부터 시작해서 주어진 policy를 따랐을 때 agent가 받을 expected discounted return이다.

💡

하지만 Value-Based Methods에서는 Policy는 학습하지 않는데 무슨 Policy를 따른 다는거죠?

• 우리는 앞서 Optimal Policy를 찾기 위해 두 가지 방법이 있다고 배웠다.
  1. Policy-Based Methods:

     

     1. Policy를 직접 학습하고 2. State가 주어졌을 때 어떤 Action 을 취해야할지 바로 학습 3. Value-Function이 없다.

  2. Value-Based Methods

     

     • Value-Based Method에서는 Policy를 직접 학습 하지 않고, state 혹은 state-action pair가 주어졌을 때 어떤 value를 가질지 학습한다. value가 주어졌을 때 해당 value를 통해 다음에 취할 Action을 결정한다.
     • Policy를 학습하지 않기 때문에 어떻게 동작해야 하는지 우리가 직접 정해줘야한다.

• 결론적으로 위 두 가지 방법 중 어느 방법으로 학습 하더라도 우리는 항상 Policy를 갖는다. 단지 Value-Based Methods 인 경우에 그 Policy는 우리가 미리 정한(pre-specified) 함수이다.

• 둘의 차이점을 아래와 같다.
  • In Policy-Based: optimal policy $\pi^*$ 는 학습을 통해 직접 구한다.
  • In Value-Based: $Q^*, V^*$ 와 같은 optimal Value function을 찾음으로 자연스럽게 이를 통해 policy도 optimal 해진다.

    

• 사실 대부분의 경우, Value-Based Methods에서는 Exploration/Exploitation trade-off를 다루는 Epsilon-Greedy Policy를 사용한다.

• 앞서 언급하였던 바와 같이 Value-Based Methods는 두 가지 종류가 있다.

The State-Value Function

• Value Function under a policy $\pi$ 를 아래와 같이 쓴다.

  

  각 스텝에 대하여, state-value function은 앞으로 모든 스텝에 대하여 주어진 policy 를 따르고 agent가 현재 state부터 시작했을 때의 expected return을 output을 갖는다.

  

  각 state마다 value값이 위 maze처럼 주어졌을 때 policy에 따라 움직이면 RRRRDDRR와 같은 순서로 움직이게 된다. (Greedy Policy)

The Action-Value Function

• Action-Value Function에서는 매 step-action pair 마다 agent가 현재 state에서 시작하고 action을 취하고, 주어진 policy $\pi$ 를 앞으로 따랐을 때의 expected return을 output으로 갖는다.

  

  

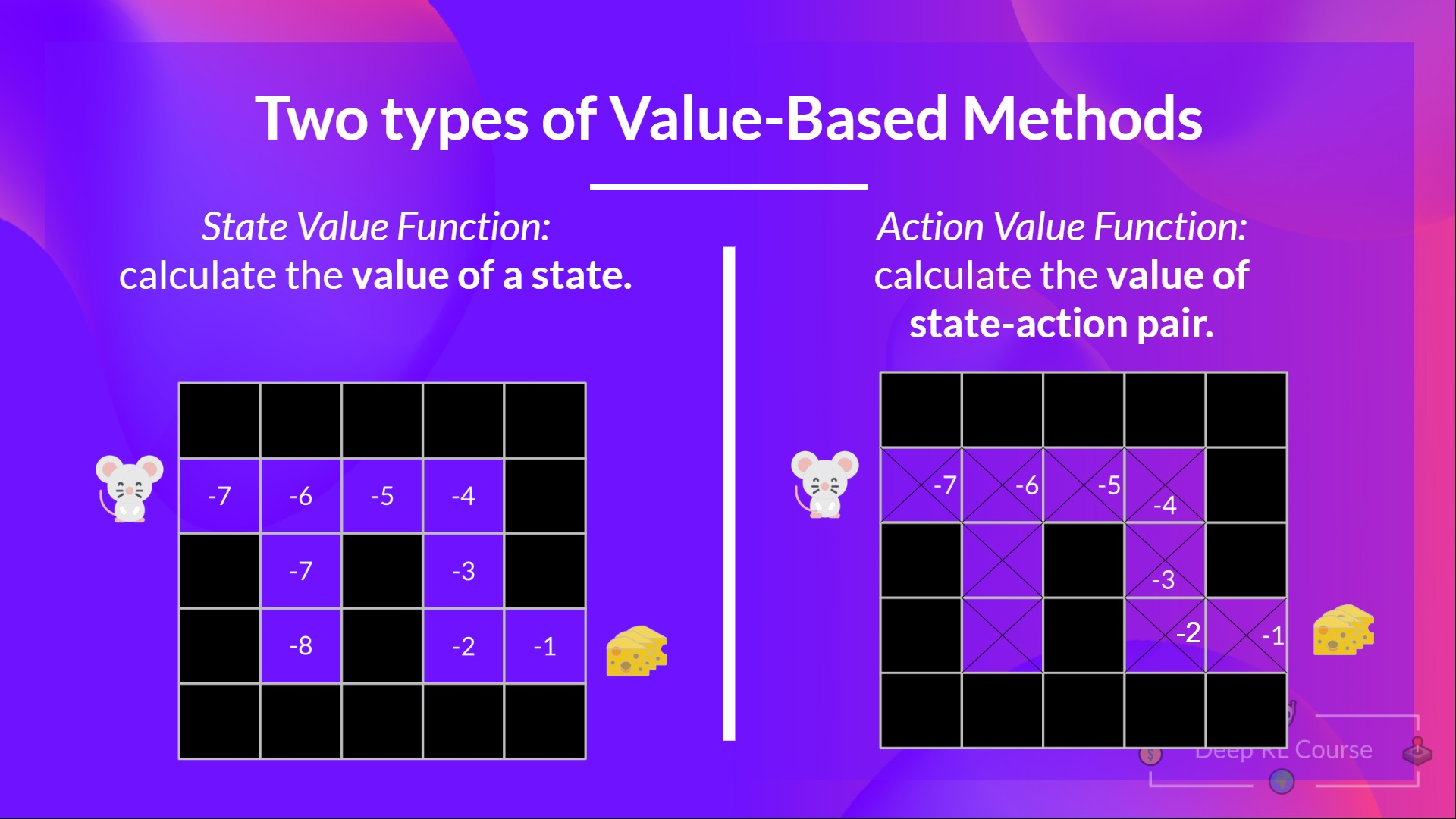
• 두 Methods의 차이점을 다음과 같다.
  • state-value function은 state $S_t$에 대해서만 expected return을 계산한다.
  • action-value function은 state-action pair ($S_t, A_t$) 에 대하여 expected return을 계산한다. 따라서 이는 주어진 state $S_t$에서 action $A_t$ 를 취했을 때의 value를 의미한다.

💡

하지만 여기서 각각의 value를 계산하는 것은 computationally expensive하다. 왜냐하면 주어진 state $S_t$ 부터 agent가 얻을 수 있는 모든 return값을 구하여 계산해야하기 때문이다. 여기서 Bellman equation이 등장한다.

• Bellman Equation은 우리의 state, action value function의 계산을 더욱 간단히 한다.

Bellman Equation

• $V(S_t)$를 계산하려면 주어진 state, action으로 부터 시작해서 return값을 계산해야한다. (예제에서는 간단히 하기 위해서 Greedy Plolicy, No discount 로 value를 계산하였다.)

• $V(S_t)$ 를 한 번 계산해보면 아래와 같이 expected return을 모두 더해야한다.

  

• 다음으로 $V(S_{t+1})$을 계산하면 아래와 같다.

  

• 위와 같이 매 state마다 이러한 return값을 계산하는 것은 그리 효율적이지 않고 지루하다.

• 따라서 이렇게 모든 state, state-action pair에 댛여 expected return을 계산하기 보다는 Bellman Equation을 사용할 수 있다.

• Bellman Equation은 매 step부터 모든 값을 계산해 나가는 대신 아래와 같이 표현하는 recursive equation이다.

  

• 따라서 처음에 구하였던 state $S_1$을 아래와 같이 단순화하여 계산할 수 있다.

  

Monte Carlo & Temporal Difference Learning

• Q-Learning을 배우기 앞서 우리가 살펴볼 마지막 내용은 두 개의 learning strategies이다.

• RL agent는 environment와 상호작용하며 학습한다. 경험(experience)과 reward가 주어졌을 때 agent가 이를 통해 value function과 policy를 update한다.

• Monte Carlo와 Temporal Difference(이하 TD)는 어떻게 value function과 우리의 policy를 학습할까에 대한 strategies이다.

• 간단히 말해서 Monte Carlo는 학습 시 모든 episode를 사용한다. 반면 TD는 딱 한 step, $(S_t, A_t, R_{t+1}, S_{t+1)}$만을 사용하여 학습한다.

Monte Carlo

• Monte Carlo는 episode가 끝날 때까지 기다리고 return $G_t$를 계산한다. 그리고 이를 $V(S_{t+1})$를 update하는 target으로 사용한다. 따라서 Monte Carlo 방식은 value function을 update하기 전에 모든 episode가 종료되어야한다.

• Example

  

  1. 항상 같은 포인트에서 episode를 시작한다.
  2. 주어진 policy대로 agent를 actions을 취한다.
  3. reward와 next state를 얻는다.
  4. 쥐가 고양이에게 잡아 먹히거나 쥐가 10step 넘어서 이동하면 episode를 종료한다.
  5. episode의 끝에 State, Actions, Rewards, Next States tuples의 list가 얻어진다.
  6. Agent가 모든 rewards $G_t$를 더하여 계산한다.
  7. 아래와 같은 식으로 $V(S_t)$를 update한다.

     

  8. 위와 같이 update된 Value function으로 새로운 게임을 시작한다.
  9. episode를 거듭하며 거듭할 수록 agent는 더욱 더 잘 플레이 하게된다.

• 예를 들어, 만약 state-value function을 Monte Carlo Method를 이용해 학습한다면,
  1. 먼저 매 step마다 0 값을 return 하도록 value function을 initialize 한다.
  2. learning rate (lr) 은 0.1로 설정하고 discount rate 은 1(No Discount)로 설정한다.
  3. 우리의 쥐가 environment를 탐험하며 random action을 취한다.

  

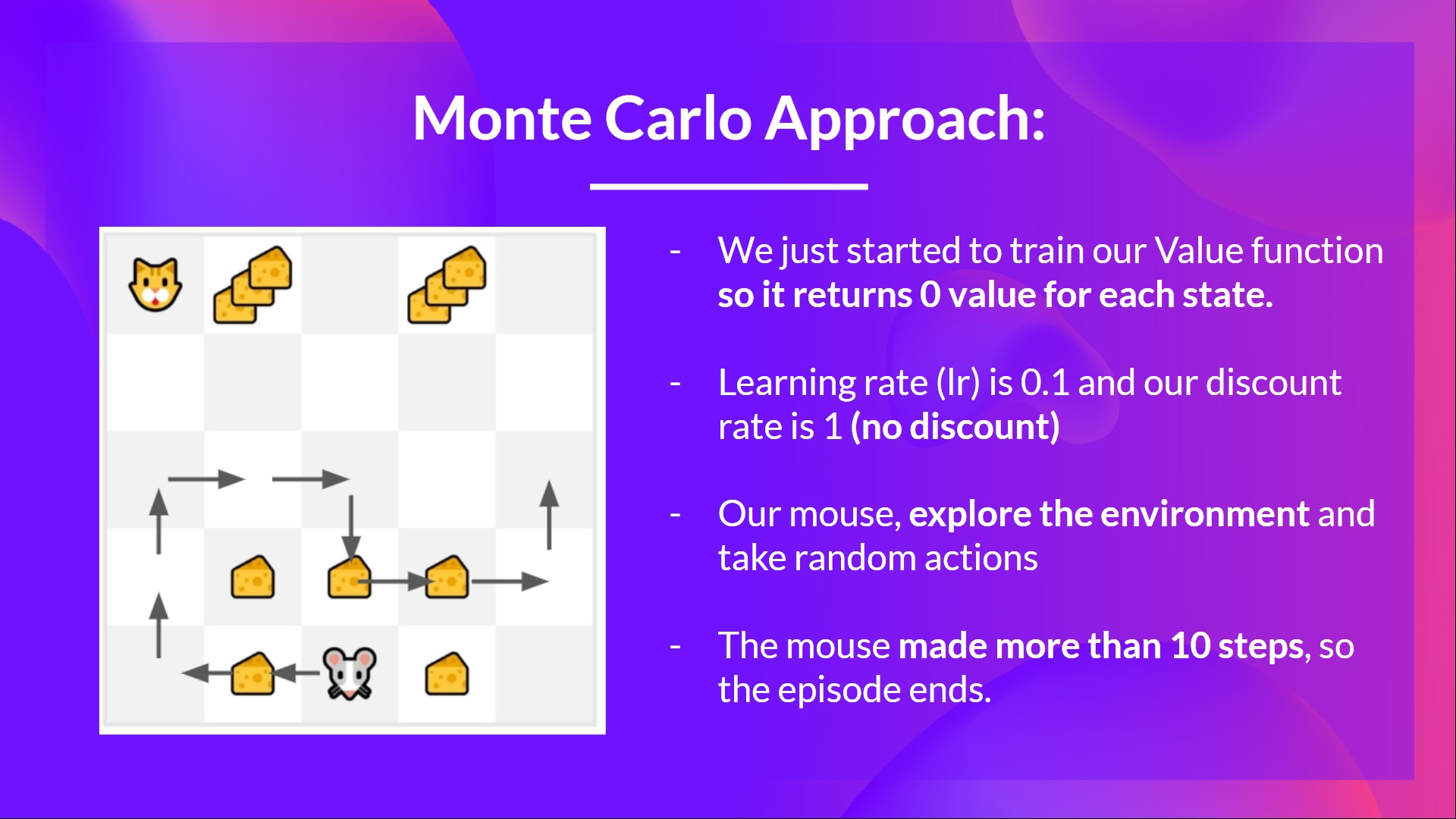
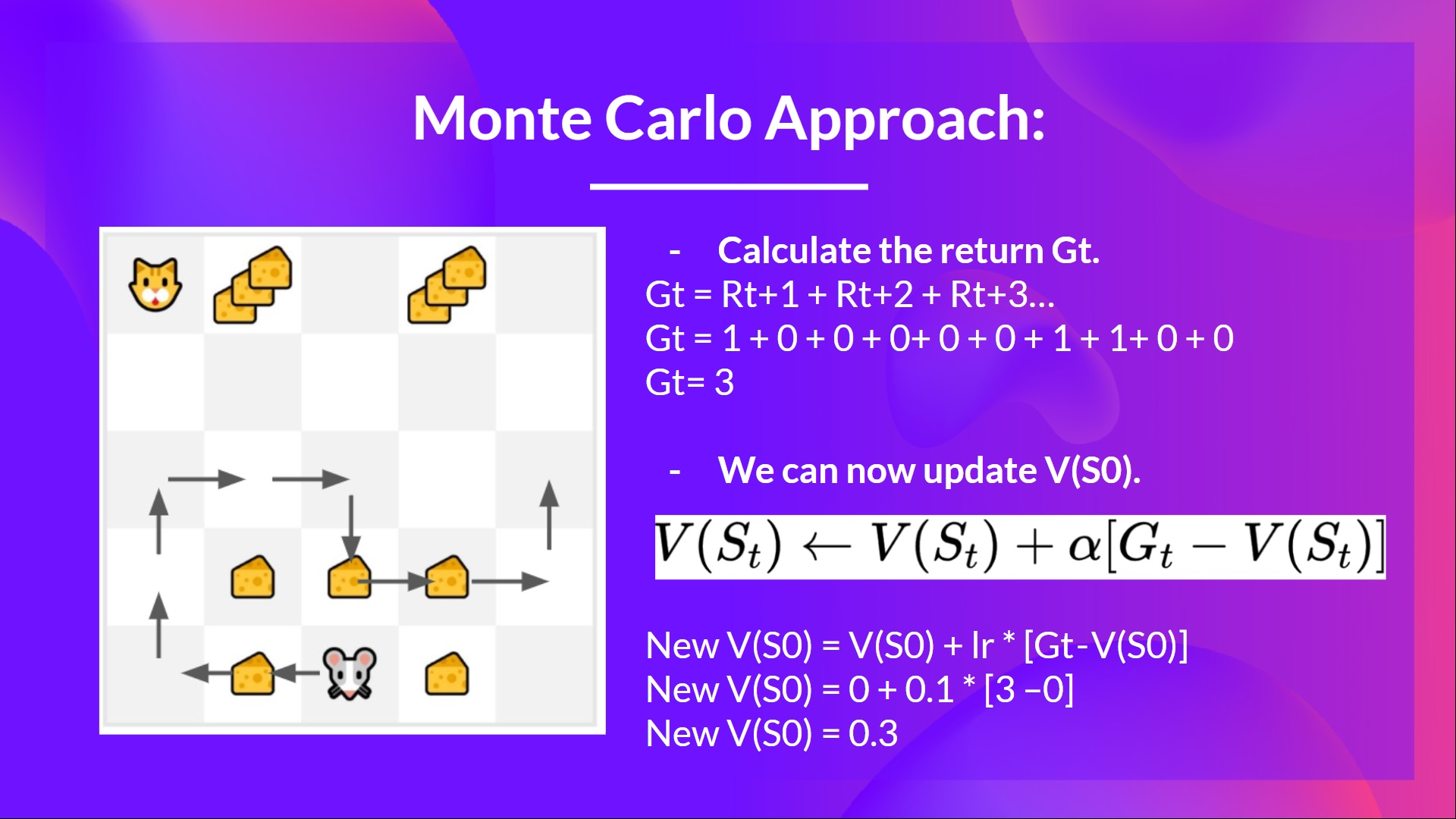
• 우리는 이때 State, Actions, Rewards, Next States를 얻고 이를 통해 return $G_t$를 계산해야한다.

  $$G_t = R_{t+1} + R_{t+2} + R_{t+3} + ...$$

  $$G_t = 1 + 0 + 0 + 0 + 0 + 0 + 1 + 1 + 0 + 0 = 3$$

• 이제 $V(S_0)$를 update 할 수 있다.

$$V(S_0) = V(S_0) + lr * [G_t - V(S_0)]$$

$$V(S_0) = 0 + 0.1 * [3-0] = 0.3$$

Temporal Difference Learning: learning at each step

• TD는 한편, TD target을 구성하고, $R_{t+1}, \gamma * V(S_{t+1})$을 사용하여 $V(S_t)$를 update 하기 위해 딱 one iteration (one step), $S_{t+1}$만을 필요로한다.

• TD의 아이디어는 매 step마다 $V(S_t)$를 update하는 것이다.

• 하지만 모든 episode를 거친 것이 아니기 때문에 $G_t$가 없다. 대신 $R_{t+1}$와 $\gamma * V(S_{t+1})$을 더하여 $G_t$를 예측한다. 이를 bootstraping 이라고 한다. 이는 TD의 update의 일부를 온전한 sample $G_t$가 아닌 기존의 $V(S_{t+1})$의 추정치에 기반하기 때문이다.

• 이와 같은 방법을 TD(0), one-step TD (매 스텝마다 value function을 update한다.) 이라고 한다.

• Monte Carlo Method에서 사용했던 example을 다시 사용한다면,

1. 모든 state 에서 0 값을 return 하도록 value-function을 initialize한다.

2. learning rate lr은 0.1, discount rate 은 1로 설정한다. (No Discount)

3. 우리의 생쥐는 environment를 탐험하기 시작한다. 그리고 random action을 취한다. (여기선 왼쪽으로 이동한다.)

4. 그러면 $R_{t+1} = 1$ 을 얻는다. (왼쪽으로 이동하면 치즈를 하나 먹을 수 있음.)

$$V(S_0) = V(S_0) + lr * [R_1 + \gamma * V(S_1) - V(S_0)]$$

$$V(S_0) = 0 + 0.1 * [1 + 1*0 - 0] = 0.1$$

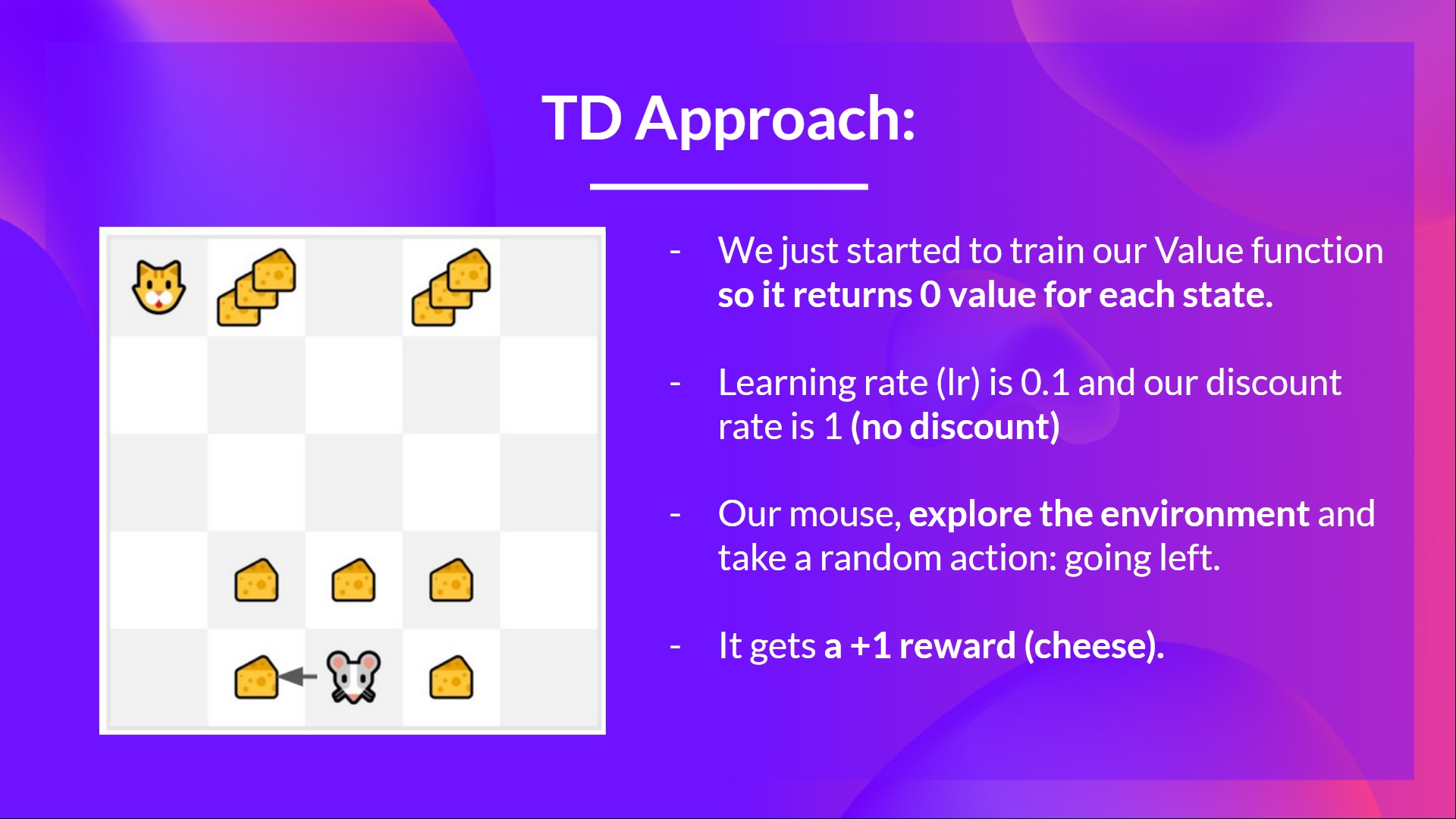
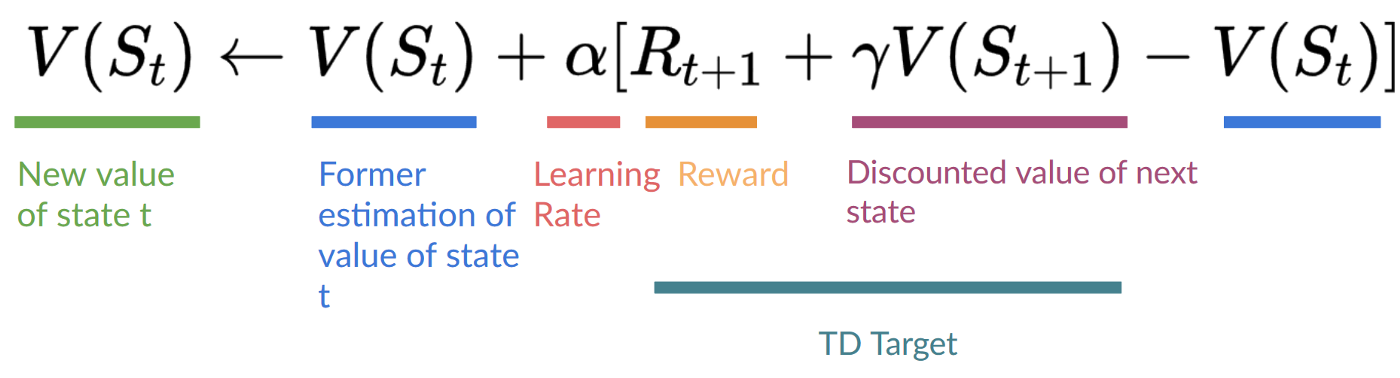
• 위와 같은 방법으로 생쥐가 모험을 더 해나갈 수록 value function이 update 된다.

Summary

• Monte Carlo Method:
  • value function을 complete episode로 update한다. 따라서 정확한 return 값으로 update할 수 있다.

• Temporal Difference: 한 step 으로부터 value function을 update 한다. TD target 이라고 불리는 estimated return을 대신 사용하여 $G_t$를 대신한다.

Intruducing Q-Learning

1. What is Q-Learning?

• Q-Learning 이란 TD approach를 사용하여 Action-Value function을 학습하는 off-policy value-based method 이다.
  • off-policy: 추후 설명 예정
  • Value-Based Method: 주어진 state, state-action pair에서의 value를 나타내는 함수인 state-value, action-value function을 학습하여 optimal policy를 간접적으로 찾는 방법
  • TD Approach: 주어진 state, state-action pair 부터 시작하여 episode의 끝까지 진행 후 학습 하는 것이 아닌 각 step을 진행하여 value function을 update

• Q-Learning은 Q-function과 주어진 state의 value와 취해야 할 action을 정하는 action-value function을 학습하기 위해 사용하는 알고리즘이다.

  

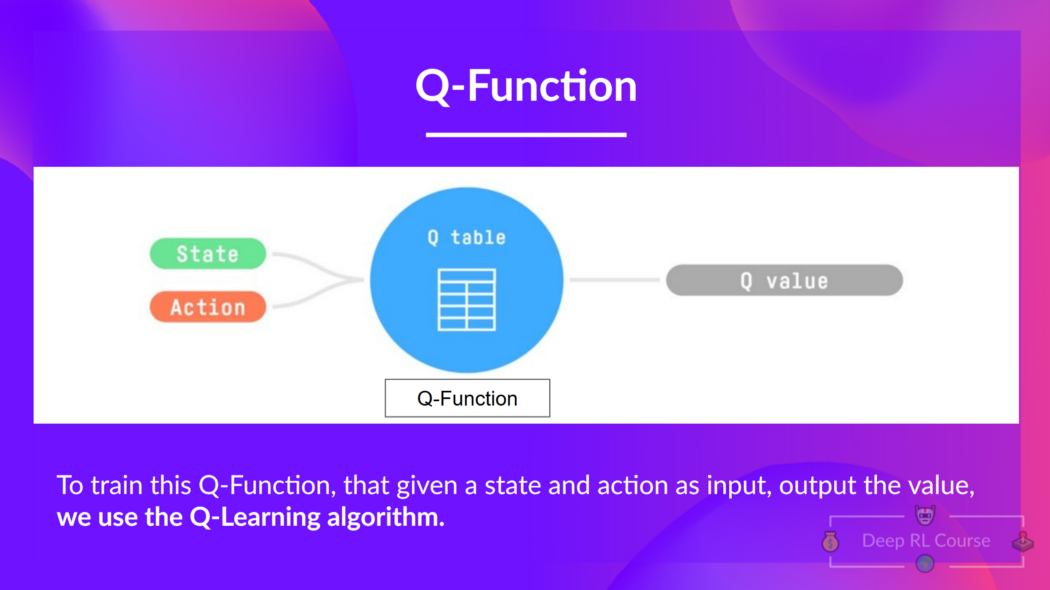
  state, action이 주어졌을 떄, Q function은 state-action value (Q-Value 라고도 불림)을 output으로 갖는다.

• Q 는 Quality에서 온 것.

• 내부적으로 Q-function은 Q-table 이라는 것으로 encode 된다. Q-table 에는 각 cell 마다 state-action pair value가 대응된다. Q-table 을 Q-function을 memory, cheat-sheet 으로 봐도 좋다.

• Example

  

1. Q-table은 initialize된 상태이다. 모든 values 가 0인 이유고, 이 table 은 각 state, action에 대응되는 state-action values 를 포함한다.

   

2. 초기 상태에서 위로 이동하는 것에 대한 state-action value 값이 0인 것을 확인 할 수 있다.

   

3. 따라서 Q-function은 각 state-action pair의 value를 갖고 있는 Q-table을 사용한다. state-action 이 주어졌을 때 Q-function은 최종 value를 구하기 위해 Q-table 의 내부를 탐색한다.

   

• Q-Learning 의 알고리즘을 나타내면 아래와 같다.
  1. Q-Function을 학습한다. 이는 내부적으로 Q-table과 동일하며 state-action pair values를 포함한다.
  2. state, action이 주어지면 Q-function은 대응되는 value를 찾기위해 Q-table을 탐색한다.
  3. 학습이 종료되면, 우리는 optimal한 Q-function, 즉 optimal한 Q-table을 갖고 있다.
  4. 만약 이 Q-function이 정말 optimal하다면, 각 state마다 어떤 action을 취하는 것이 best인지 알기 때문에 optimal 한 policy를 찾았다고 할 수있다

     

• Q-function은 학습 초기에는 주어진 state, action에 대하여 임의의 values 값을 return할테지만 학습을 거듭하며 optimal policy에 점점 근사해질 것이다.

Q-Learning Algorithm

• 아래 이미지는 Q-Learning 의 pseudocode 이다.

  

1. Step 1: Q-table을 initialize 한다.

   

   각 state-action pair에 대하여 values를 초기화한다. 대부분의 경우 0들로 초기화한다.

2. Step 2: Choose an action using the epsilon-greedy strategy

   

   • The epsilon-greedy strategy는 exploration/exploitation의 trade-off를 핸들링하는 policy이다.
   • Epsilon-Greedy Strategy
     • $\epsilon=1.0$ 으로 초기화 한다.
     • $1-\epsilon$ 의 확률로, exploitation 한다. (agent가 가장 높은 state-action value를 갖는 action을 취한다.)
     • $\epsilon$ 의 확률로, exploration 한다. (agent가 random action을 취한다.)
     • 학습 단계 초기에는 $\epsilon$이 매우 높기 때문에 대부분의 경우 exploration을 한다. 하지만 학습이 진행되고 우리의 Q-table이 더욱 더 좋은 estimation을 냄에 따라 점점 $\epsilon$ 값을 줄여나간다. 왜냐하면 exploration 보다는 exploitation을 하기를 원하기 때문이다.

     

3. Step 3: action $A_t$를 수행하고, reward $R_{t+1}$와 next state $S_{t+1}$를 얻는다.

   

4. Step 4: $Q(S_t, A_t)$를 update 한다.
   • TD learning에서는 value function 혹은 policy를 update 하기 위해 one step of interaction 뒤에 바로 한다는 것을 기억하기 바란다.
   • TD Target 을 구하기 위해 immediate reward $R_{t+1}$ 와 discounted value of next state $\gamma * V(S_{t+1})$ 를 더한 값을 사용한다.

     

   따라서 $Q(S_t, A_t)$ update formula는 아래와 같이 정리될 수 있다.

   

   • 그렇다면 TD Target 을 어떻게 구할 수 있을까?
     1. action을 취하고 reward $R_{t+1}$을 얻는다.
     2. next state에 대하여 best state-action pair value를 얻기 위해 우리는 이때만큼은 Greedy Policy를 사용한다. 이는 Epsilon-Greedy Policy가 아니며 가장 높은 state-action value를 갖는 action을 취한다.

• 위와 같은 방식으로 Q-Value를 update하고 새로운 state 에서는 Epsilon-Greedy Policy를 사용하여 다음 action을 결정한다.

• Q-Learning이 Off-Policy Algorithm이라고 불리우는 이유이다.

Off-Policy vs On-Policy

• 차이는 미묘함
  • Off-Policy: acting(inference), updating(training) 에 서로 다른 policy를 적용하는 것.
    • 예를 들어 Q-Learning 에서는 acting policy로는 Epsilon-Greedy Policy를, training policy로는 Greedy-Policy를 쓴다.

      

  • On-Policy: acting, updating에 서로 같은 policy를 적용하는 것
    • SARSA 같은 또 다른 value-based algorithm은 acting, updating 에 모두 Epsilon-Greedy Policy를 사용한다.

Q-Learning Example

간단한 예제를 살펴보자

1. 당신은 생쥐고 미로에 갖혀있다. 또 매번 같은 starting point 에서 시작한다.

2. 목표는 우하단에 있는 치즈 더미를 먹는 것이다.

3. episode의 end 조건은 5step 보다 더 이동하던가, poison을 먹던가 치즈 덩어리를 먹는 경우이다.

4. $lr = 0.1, \gamma = 0.99$

• reward는 아래와 같다.

  

• 위 RL problem을 해결하기 위해 Q-Learning Algorithm을 사용

Step 1: Q-table 초기화

• 현재의 Q-table 은 쓸모가 없다. 이를 학습시켜보자

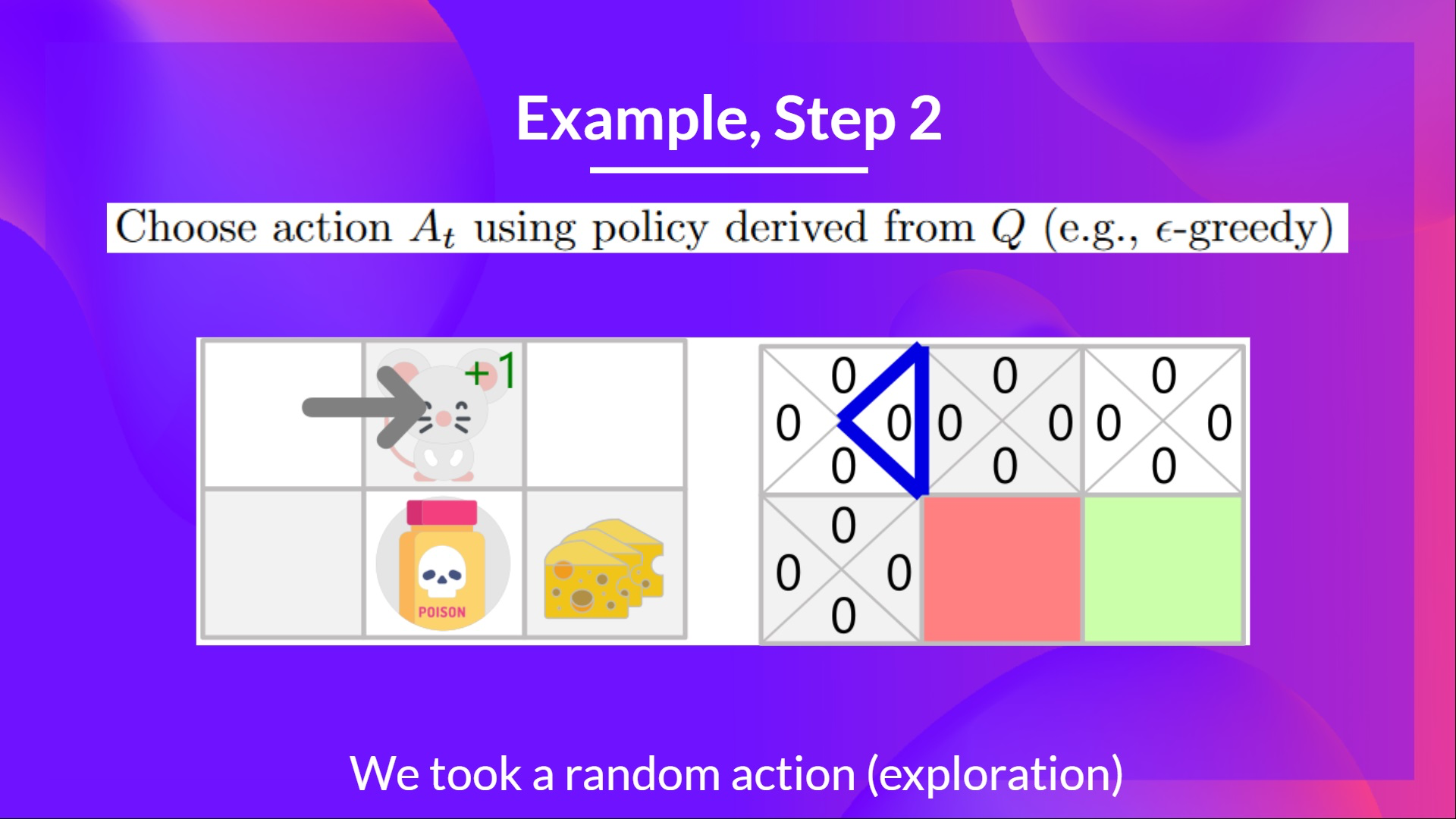
Step 2: Epsilon-Greedy Strategy를 사용하여 action을 선택

• $\epsilon = 1.0$ 이기 때문에 여기서는 random action을 취한다. (본 예제에서는 오른쪽 선택)

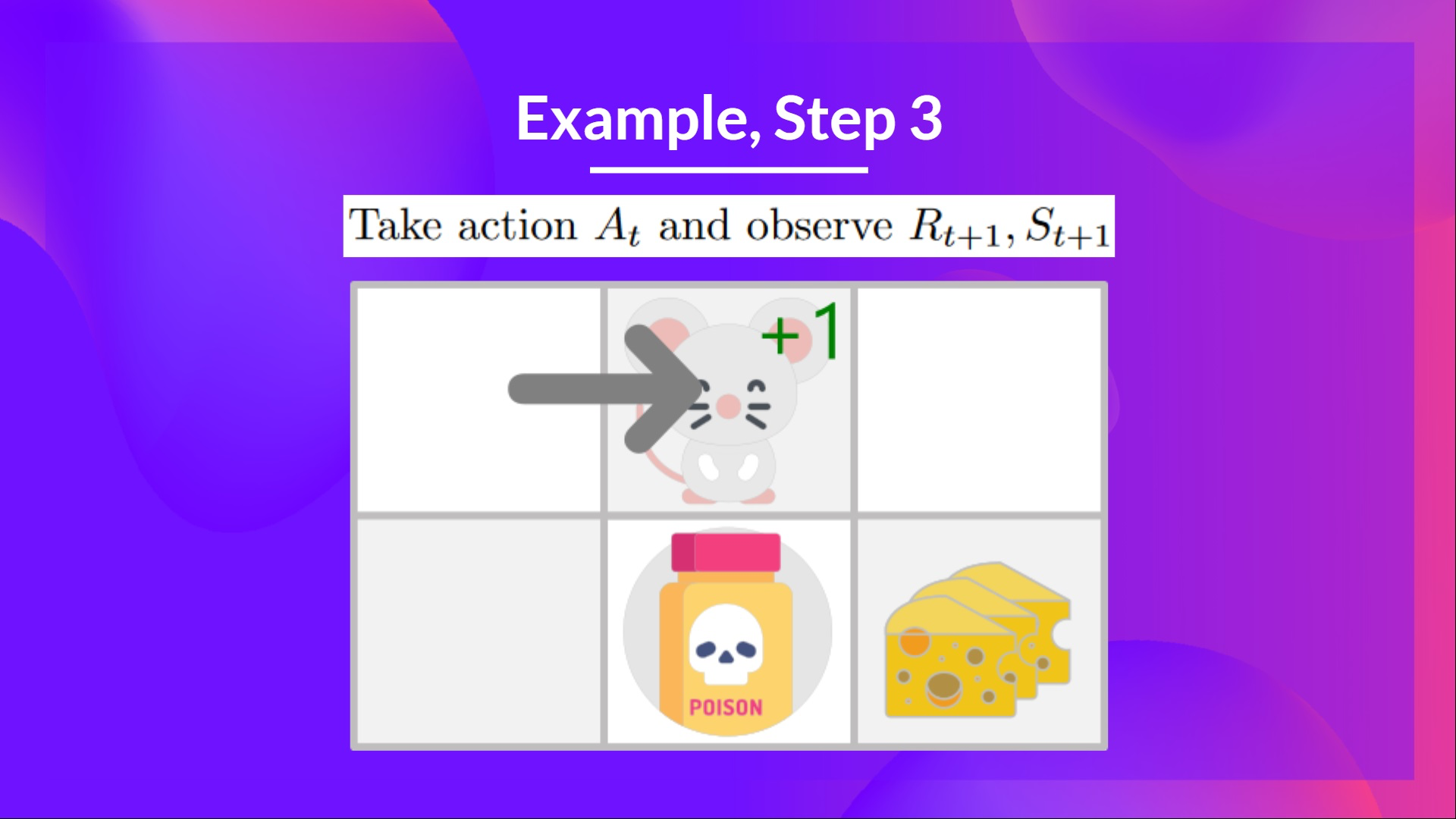
Step 3: action $A_t$를 수행하고, reward $R_{t+1}$, Next State $S_{t+1}$를 얻음

• 오른쪽으로 이동했기 때문에 치즈 한덩이를 먹을 수 있었다. 따라서 $R_{t+1} = 1$ 과 next state를 얻는다.

Step 4: $Q(S_t, A_t)$를 update 한다.

두번째 Training Timestep 진행.

Step 2: Epsilon-Greedy Strategy를 사용하여 action을 선택

• $\epsilon = 0.99$ 쯤으로 아직도 아주 높기 때문에 다시 한 번 random action을 취한다. 여기서는 아래로 이동했다고 생각하자.

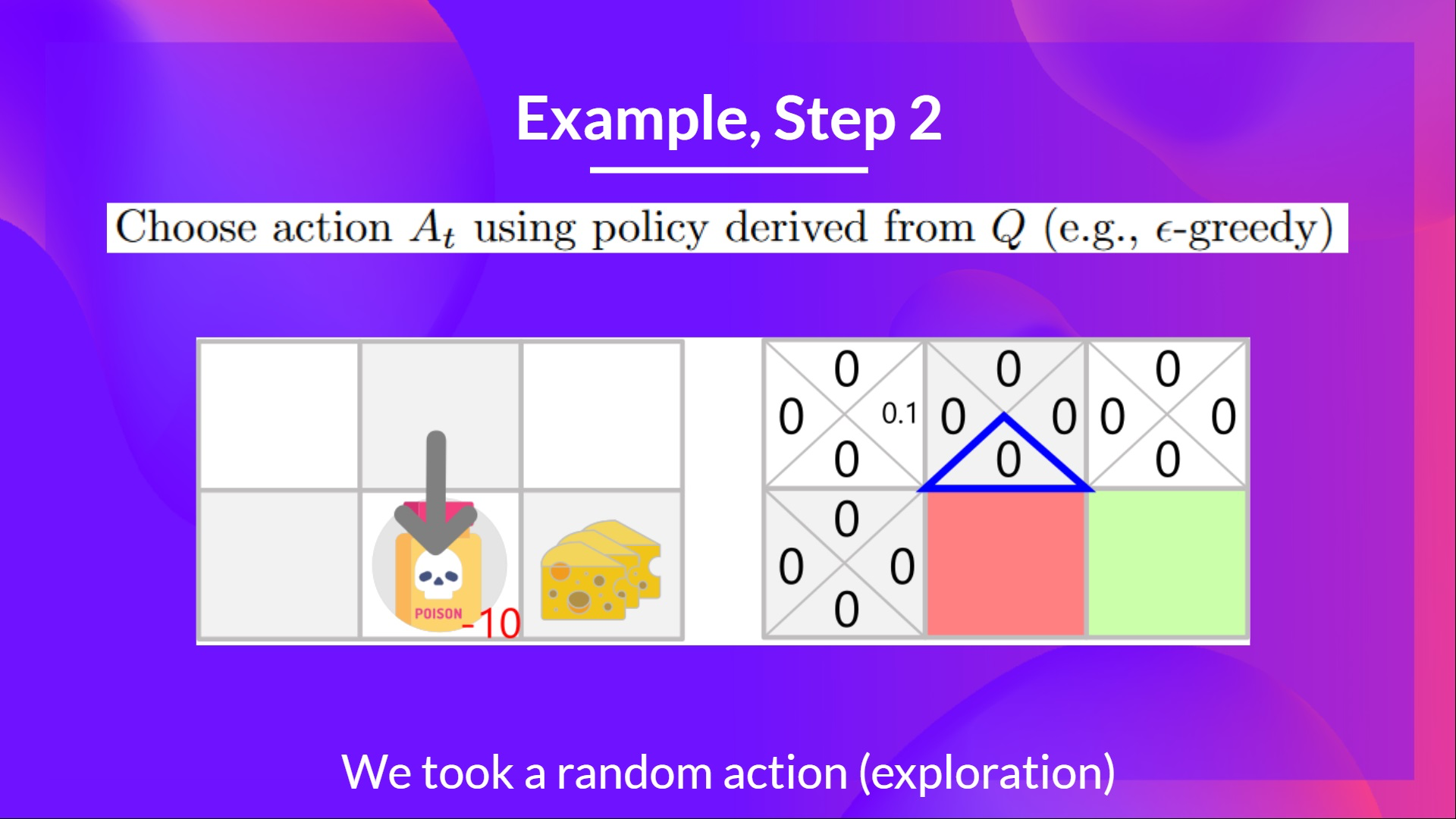
Step 3: action $A_t$를 수행하고, reward $R_{t+1}$, Next State $S_{t+1}$를 얻음

• poison을 먹었기 때문에 $R_{t+1} = -10$ 을 얻는다.

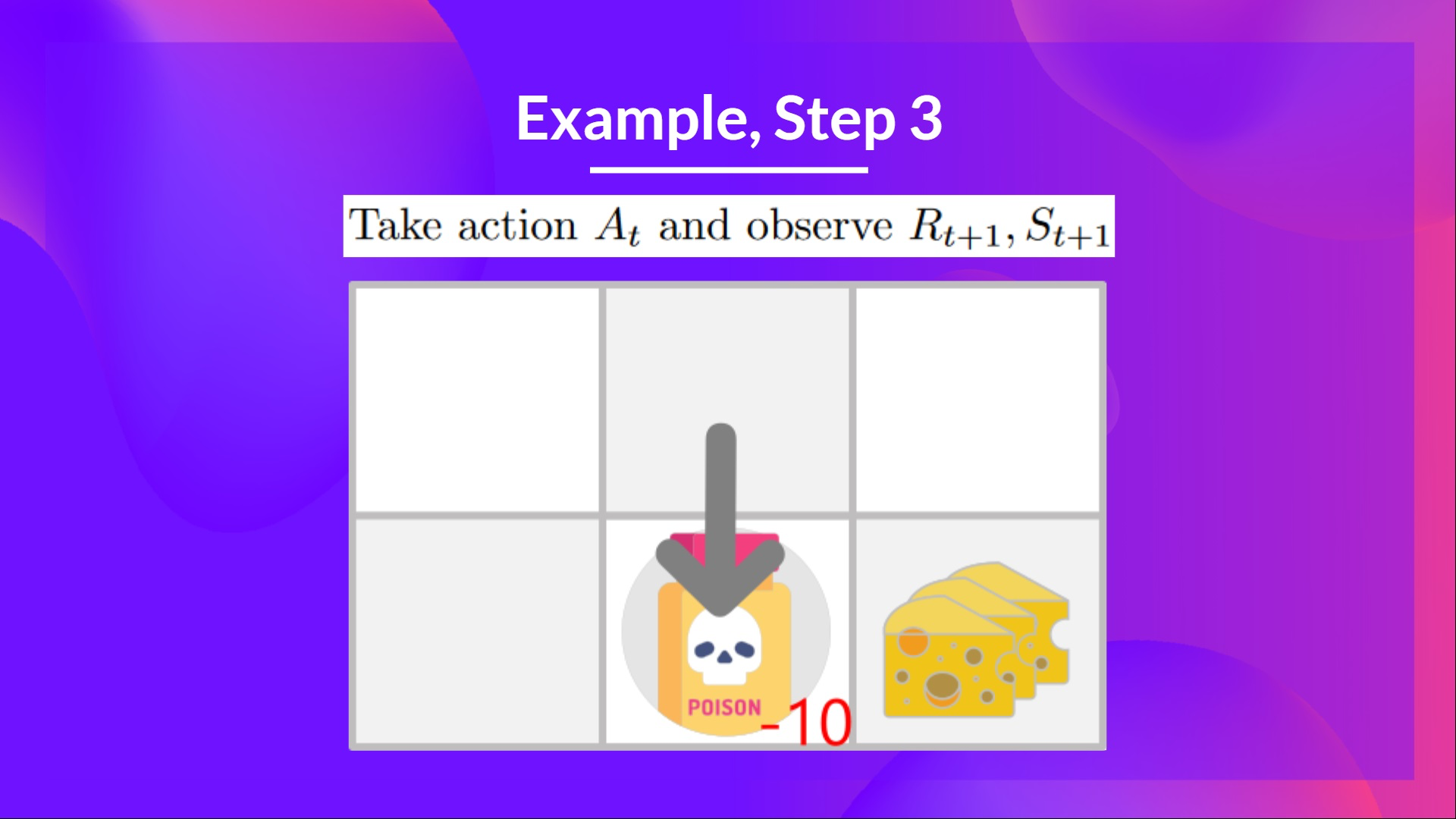
Step 4: $Q(S_t, A_t)$를 update 한다.

• 이렇게 episode가 종료된다. 이제 새로운 episode를 시작해야한다. 오직 2steps의 exploration이 있었지만 Q-table을 보면 우리의 agent 가 아주 조금은 똑똑해질 것이라는 것을 알 수 있다.

Uploaded by N2T