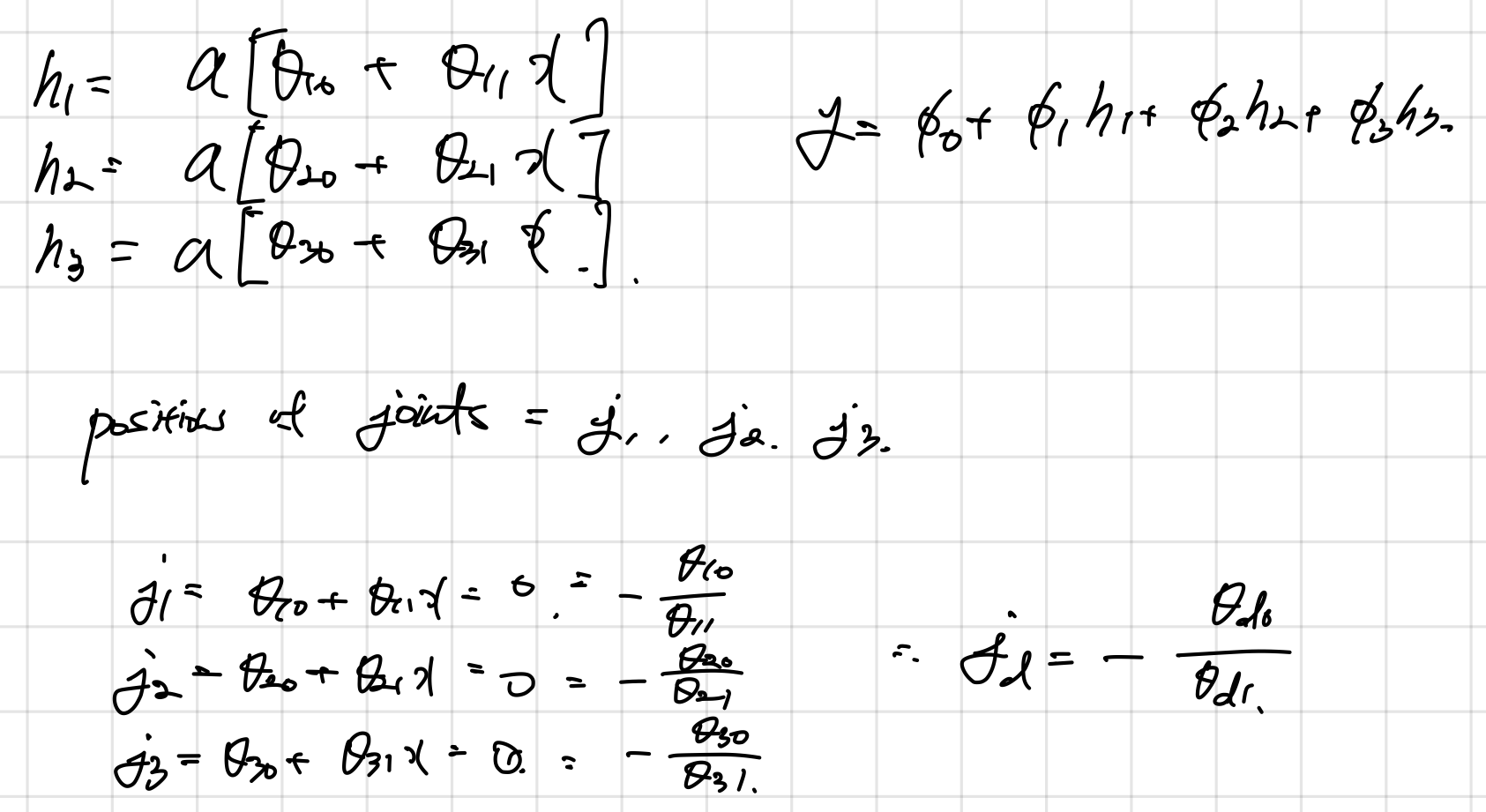Shallow Neural Networks

본 포스팅은 Simon J.D. Prince 의 Deep Learning 교재를 스터디하며 정리한 글임을 밝힙니다.

https://udlbook.github.io/udlbook/

Chapter 2에서는 1D linear regression 활용한 supervised learning 을 소개한다. 하지만 이러한 모델은 입력/출력의 관계를 하나의 “line” 으로만 표현한다. 본 챕터에서는 이러한 “lines” 는 “piecewise linear funcsion(조각 선형함수?)” 로 표현될 수 있고, 이들은 임의의 복잡한 고차원의 입력/출력의 관계를 표현하기에 충분하다는 것을 보인다.

3.1. Neural network Example

Shallow neural networs 는 multivariate inputs $\bold{x}$를 output, $\bold{y}$ 에 맵핑하는 파라미터 $\phi$ 로 구성된 함수, $\bold{y=f[x, \phi]}$ 이다. 이들의 풀 정의는 3.4.에서 할거고 그 전에 먼저 scalar input, output, $x, y$, 를 맵핑하는 10개의 파라미터, $\{\phi_0, \phi_1, \phi_2, \phi_3, \theta_{10}, \theta_{11}, \theta_{20}, \theta_{21}, \theta_{30}, \theta_{31}\}$ 로 구성된 네트워크 $f[x, \phi]$ 를 통해 메인 아이디어를 소개한다. 먼저 아래와 같이 정의된다.

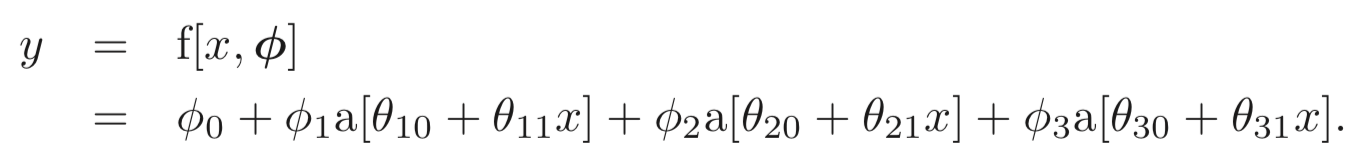
위 식의 계산을 3단계로 나누어 볼 수있다.

1. 입력 데이터의 3개의 linear functions, $(\theta_{10}+\theta_{11}x), (\theta_{20}+\theta_{21}x), (\theta_{30}+\theta_{31}x)$.

2. 위에서 계산한 3개의 linear function을 activation function, $a[\bullet]$에 먹인다.

   

   다양한 activation funcionts 중 일부

3. activation function을 통과한 3개의 중간 결과들을 $\phi_0, \phi_1, \phi_2, \phi_3$ 로 weighted sum 한다.

activation function으로는 다양한 선택지가 있는데, 우리는 그 중에서 rectified linear unit, ReLU를 사용한다. ReLU는 아래와 같이 정의된다.

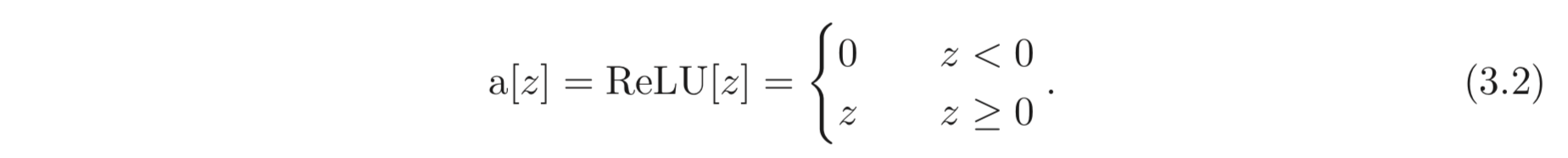
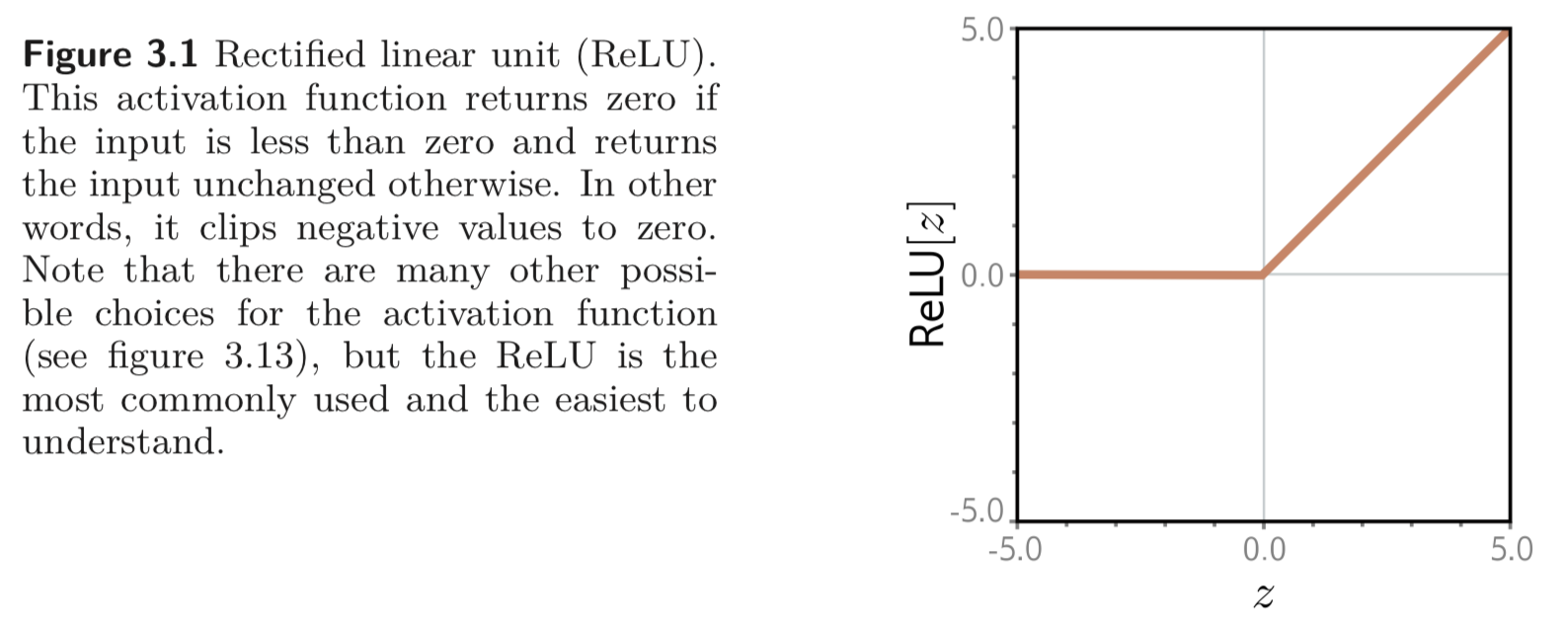
ReLU는 input이 0보다 작으면 0을, 그렇지 않으면 input 그대로를 return 한다. 첫 번째 식을 보면 어떤 식이 (family of equations) 입력/출력의 관계를 나타내는지 구분하기 어려운데, 그냥 모든 10개의 파라미터들에 대한 식, $\bold{\phi}$, 로 구성되어 입력/출력의 관계를 정의한다고 이해하도 좋다.

만약 우리가 모든 파라미터를 알고 있다면 $y$를 예측 (inference)할 수 있다. 그렇다면 주어진 dataset, $\{x_i, y_i\})_{i=1...I}$ 에 대해서 파라미터 $\phi$가 이들을 얼마나 잘 정의하는지에 대한 L2 Loss, $L[\phi]$도 구할 수 있다. 그리고 이러한 평가 지표에 따라 이러한 loss를 최소화 하는 최적의 파라미터, $\hat{\phi}$ 도 찾을 수 있다.

3.1.1. Neural Network Intuition

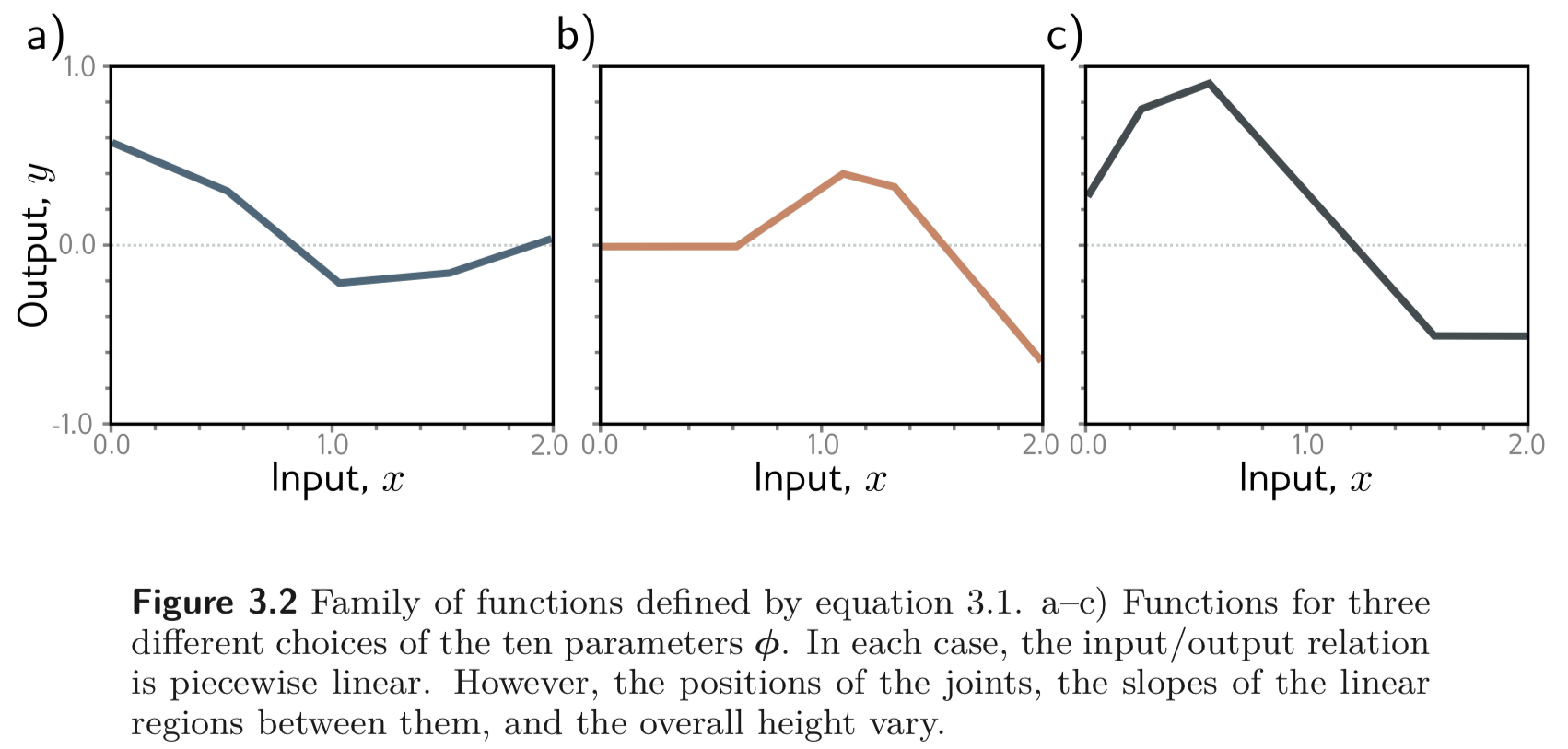
사실 첫번째 식은 최대 4개의 linear regions 을 가질 수 있는 continuous piecewise linear functions 을 나타낸다. 아래 Figure를 보라. (각각의 region을 하나의 member of family of equations으로 봐도 좋다.)

왜 저렇게 되는지 설명하기 위해 첫번째 식을 2단계로 다시 나눈다. 먼저, 아래와 같은 중간 값들을 먼저 소개한다.

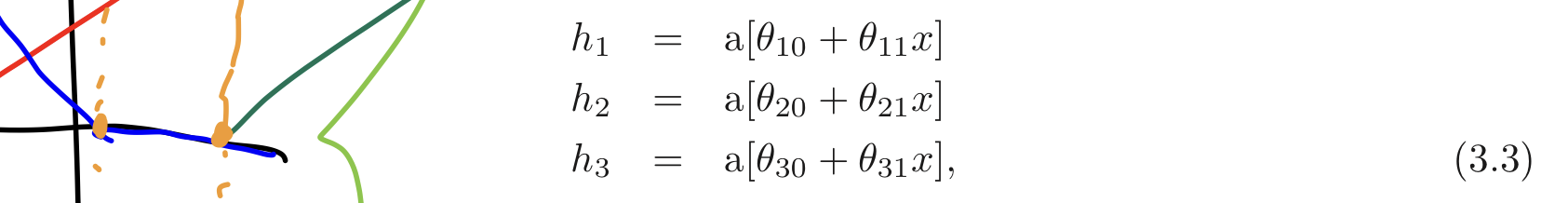
우리는 $h_1, h_2, h_3$를 hidden units 라고 부른다. 둘째로 앞서 계산한 hidden units들을 line functions로 계산하여 최종 출력을 계산한다.

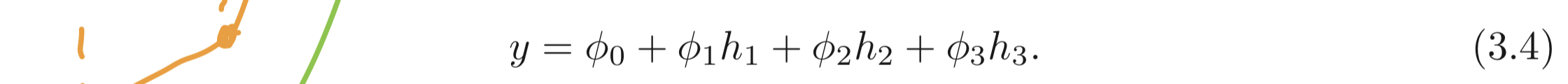
Equation 3.3 에서 계산된 hidden units들은 먼저 입력, $x$를 linear function, $\theta_{\bullet0} + \theta_{\bullet1}x$ 으로 계산하고, 이 결과가 0보다 작은 부분을 clip하는 activation function, ReLU function, $a[\bullet]$ 에 통과시킨 값이다.

이때, 이 3개의 linear function으로 그려진 lines (Figure 3.3의 [a-c])가 0을 지나는 점들은 “joints” 가 된다. 그리고 clip된 3개의 lines (Figure 3.3.의 [d-f]) 는 $\phi_0, \phi_1, \phi_2, \phi_3,$ 들로 weighted sum (Figure 3.3 [g-i]) 되어 최종 결과 (Figure 3.3 [j]) 를 계산한다.

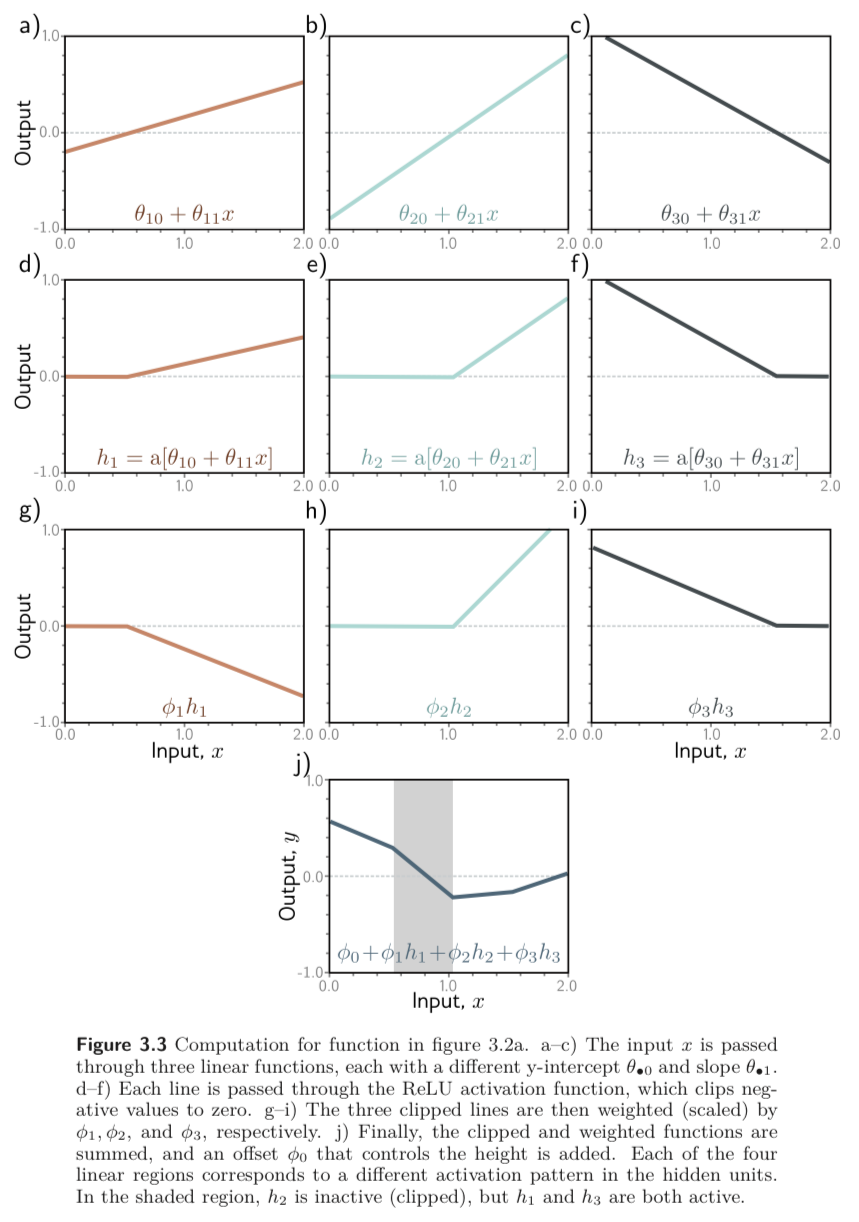
각 linear regions (3.3 j에서 평평한 부분들) 들은 각기 다른 activation pattern 에 대응된다. 중간 값은 hidden unit, $h_i$ 값이 clip 된 부분을 inactive 되었다 라고 하고 나머지 살아난 부분을 active 되었다 라고 한다. 예를 들어 3.3의 회색으로 칠해진 부분은 $h_1, h_3$ 의 contributions을 받는다 (active). $h_2$는 inactivate.

정리하자면, 3개의 hidden units, $h_1, h_2, h_3$는 3개의 “joints” 에 contribute 하기 때문에 4개의 linear regions 이 생길 수 있다. 하지만 3개의 linear regions만 independent하고, 남은 하나는 아니다. 모든 hidden units이 inactive 되어 0이거나 다른 영역들의 합이기 때문이다.

3.1.2. Depicting Neural Networks

3.1.1. 에서는 scalar input, $x$, scalar output, $y$ 를 맵핑하는 3개의 hidden units을 갖는 모델을 디자인하였다. 이들은 아래와 같이 표현된다.

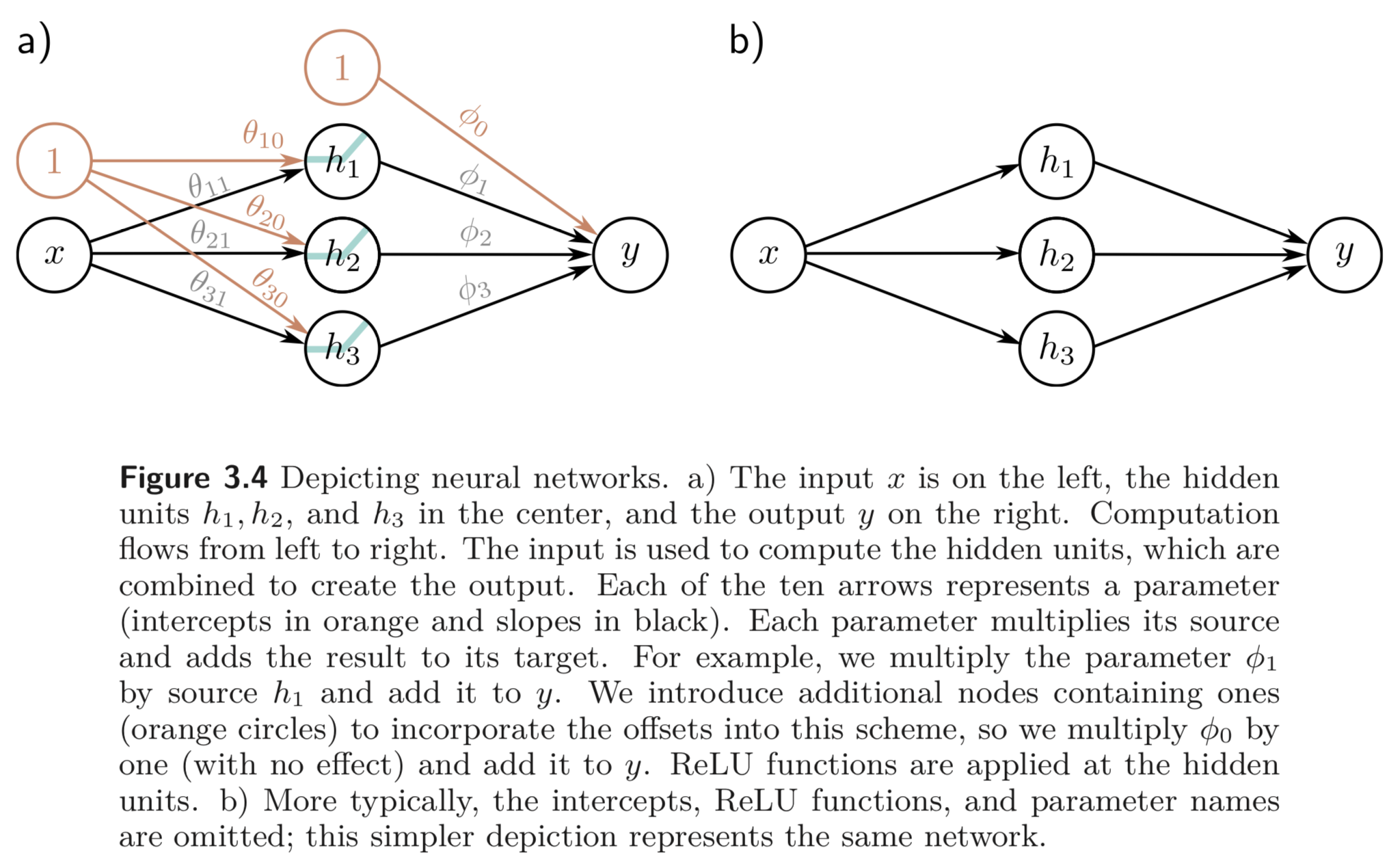
3.1.1. 에서는 offset(=bias) term 이 있어 3.4 a) 에서는 이를 표현해줬지만 보통은 bias term은 빼고 모델을 표현한다.

3.2. Universal Approximation Theorem

3.1. 에서 예제로 살펴보았던 모델을 hidden units의 갯수를 $D$ 개로 확장하여 이를 일반화한다. d번째 hidden unit과 최종 출력은 아래와 같이 계산된다.

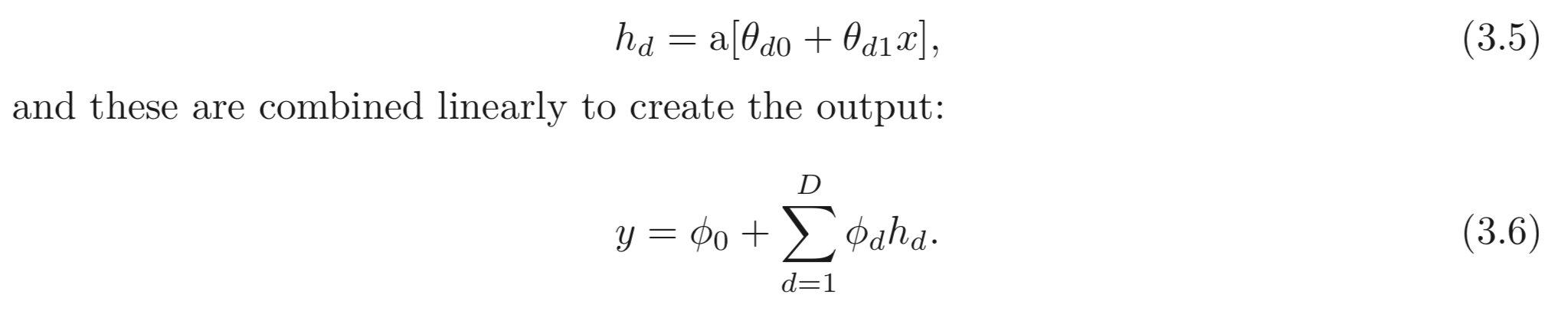
shallow network에서 hidden units의 갯수는 network capacity의 평가 지표가 된다. ReLU activation 을 쓴다면, $D$개의 hidden units 는 $D$개의 joints를 갖고 $D+1$개의 piecewise linear regions를 갖는다. $D$가 커지면 커질 수록 더욱 복잡한 함수를 approximation 할 수 있다.

충분히 큰 capacity, ($\propto$ # of hidden units), 를 갖는 shallow network는 어떠한 복잡한 1D continuous function 이라도 이 함수의 compact subset을 나타낼 수 있다. (완전히 같지는 않지만 대부분의 점에서 real line 을 따르는, 그래서 subset 이라는 표현을 쓰고 거의 비슷하니까 compact라고 한듯)

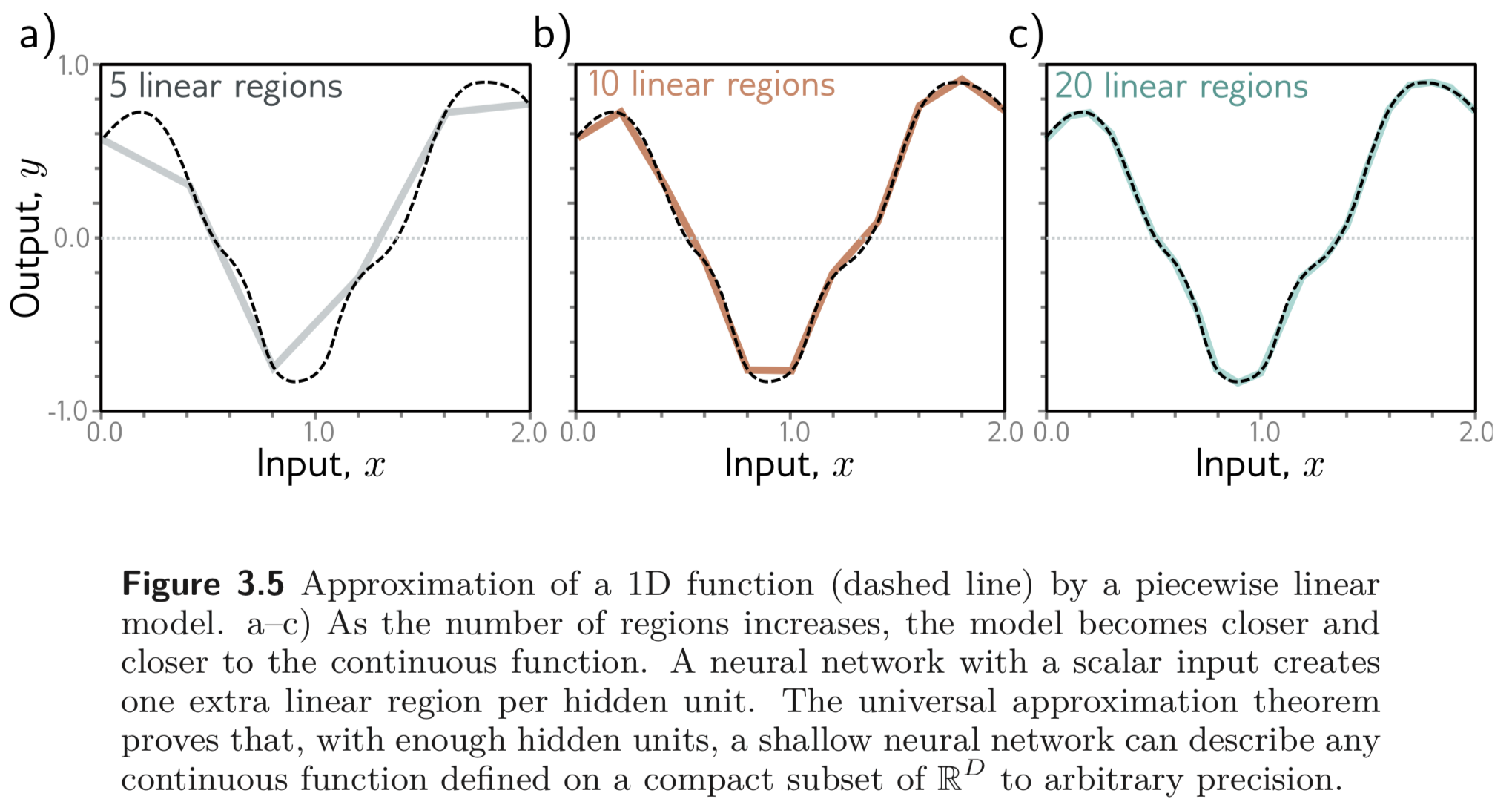
위와 같은 직관으로부터 시작하여, 어떠한 continuous functions 이라도 neural network가 이를 approximate 할 수 있다는 것은 수식으로 증명이 가능한데, 이를 Universal Approximation Theorem이라고 한다.

3.3. Multivariate Inputs and Outputs

3.1-2. 의 예제에서는 스칼라 입력/출력 에 대한 network를 다루었다. Universal approximation theorem은 multivariate 입력, $\bold{x}=[x_1, x_2, ..., x_{D_i}]^T$ /출력, $\bold{y}=[y_1, y_2, ..., y_{D_o}]^T$ 에 대해서도 여전히 성립한다 (hold). 본 섹션에서는 어떻게 모델을 multivariate output을 출력하는지에 대해서 살펴보고, 다음으로 multivariate 입력에 대해서 살펴본다. 3.4. 에서는 이러한 shallow neural network 에 대한 general definition을 정의한다.

3.3.1. Visualizing Multivariate Outputs

기존의 방법을 multivariate output, $\bold{y}$ 에 대한 모델로 확장시키기 위해서, 간단히 각 output을 계산하기 위해 서로 다른 linear function을 hidden units에 대하여 사용한다. 스칼라 입력, $x$ 가 있고, 4개의 hidden units 이 있다. 그리고 출력은 2D multivariate output, $\bold{y}=[y_1, y_2]^T$ 인 모델을 아래와 같이 정의할 수 있다.

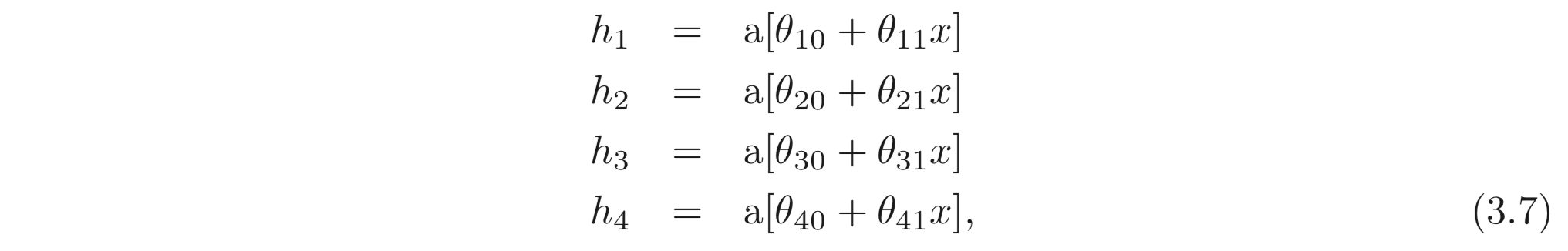
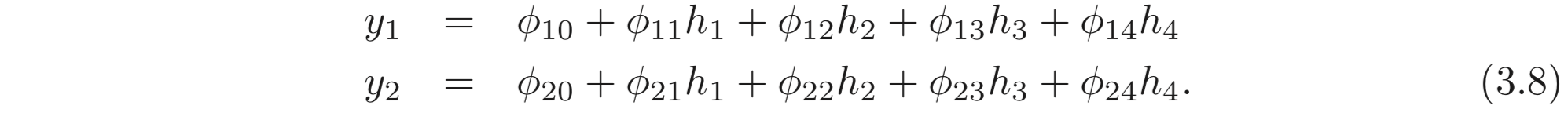
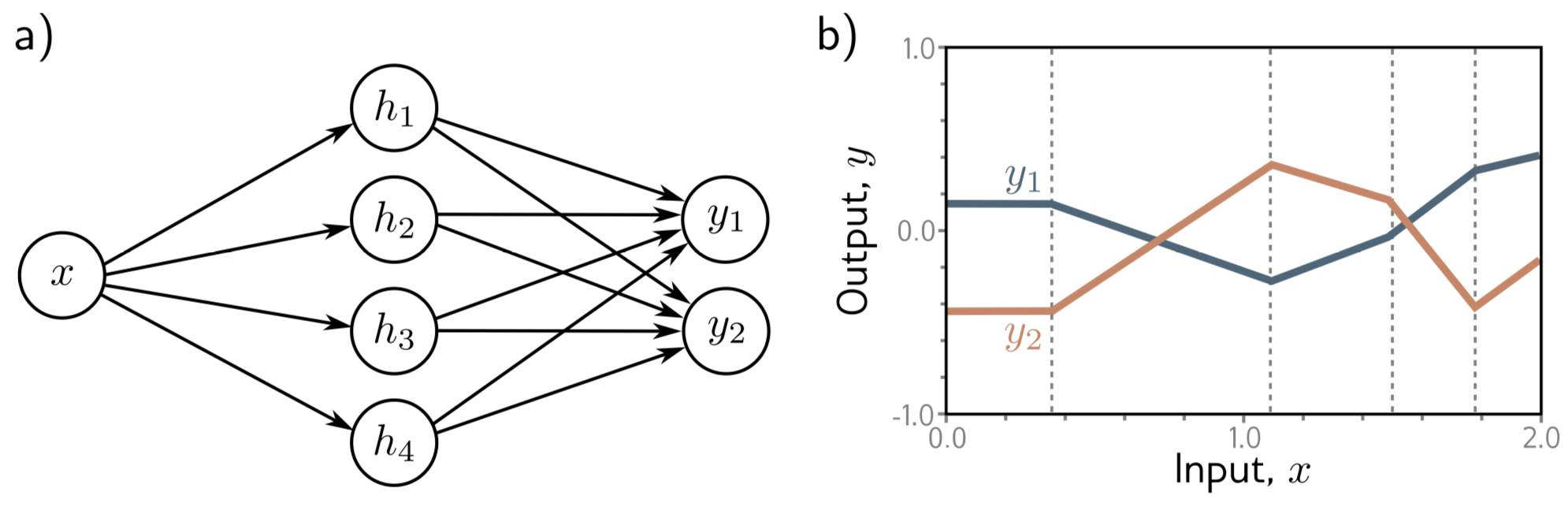
2개의 출력, $y_1, y_2$는 hidden units의 서로 다른 두 linear functions의 결과이다.

앞서 살펴 보았듯이, “joints”는 hidden units의 갯수로 결정된다. 각각의 결과 $y_1, y_2$는 서로 같은 hidden units를 사용하여 계산되기 때문에 이 joints의 포인트는 둘 다 같다. 하지만 서로 다른 linear functions을 사용하기 때문에 각 linear regions의 slopes이 다르다. 아래 figure를 보자.

3.3.2. Visualizing Multivariate Inputs

multivariate 입력, $\bold{x}$을 나타내기 위해, 입력과 hidden units의 선형 관계를 확장해야한다. 아래와 같이 2D multivatiate input, $\bold{x}=[x_1, x_2]^T$, 와 3개의 hidden units, 스칼라 출력, $y$로 정의된 모델은 아래와 같이 정의할 수 있다.

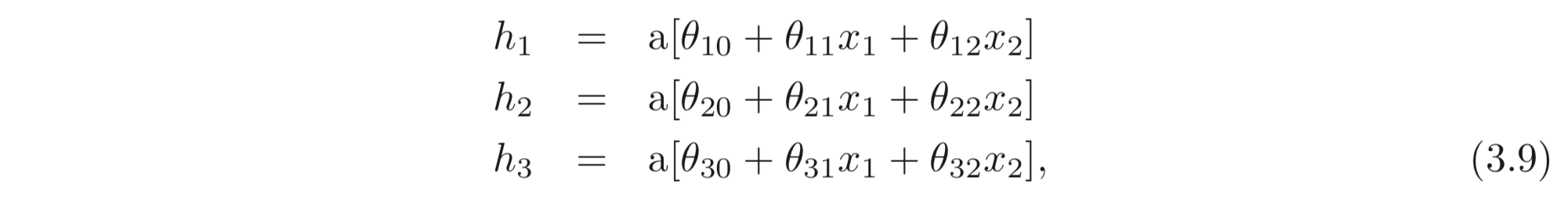
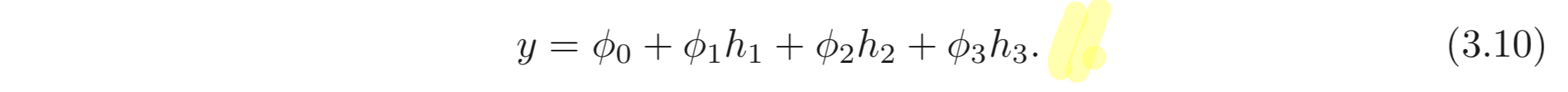
아래 Figure는 이와 같은 network의 processing 과정을 보인다.

먼저 [a-c]를 보면 각 3개의 hidden units는 2개의 input, $x_1, x_2$의 linear combination을 받고, 이는 3차원 상에서 input/output pair를 만들어낸다.

[d-f] 는 [a-c]에서 계산된 hyperplane 을 음수는 0으로 return하여 clip 한 결과를 보인다. 이렇게 clip된 평면들은 Equaion 3.10의 linear function의 파라미터들에 의해 weighted 되고 [g-i], 더해져서 최종 결과인 [j] 와 같은 convex polygonal regions (linear regions의 3D 버전) 를 만들어 낸다.

여기서 주목할 점은, input의 dimension이 늘어나면 linear regions의 갯수도 급격하게 증가한다는 점이다. 얼마나 빨리 증가하는지 느껴보기 위해 각 hidden unit이 active되는 공간을 나타내는 hyperplane을 나타낸다고 생각해보자. 만약 hidden units의 갯수가 input dimension이 $D_i$와 같다면, 우리는 이러한 hyperplane을 각 축에 대응할 수 있다. (See Figure 3.10)

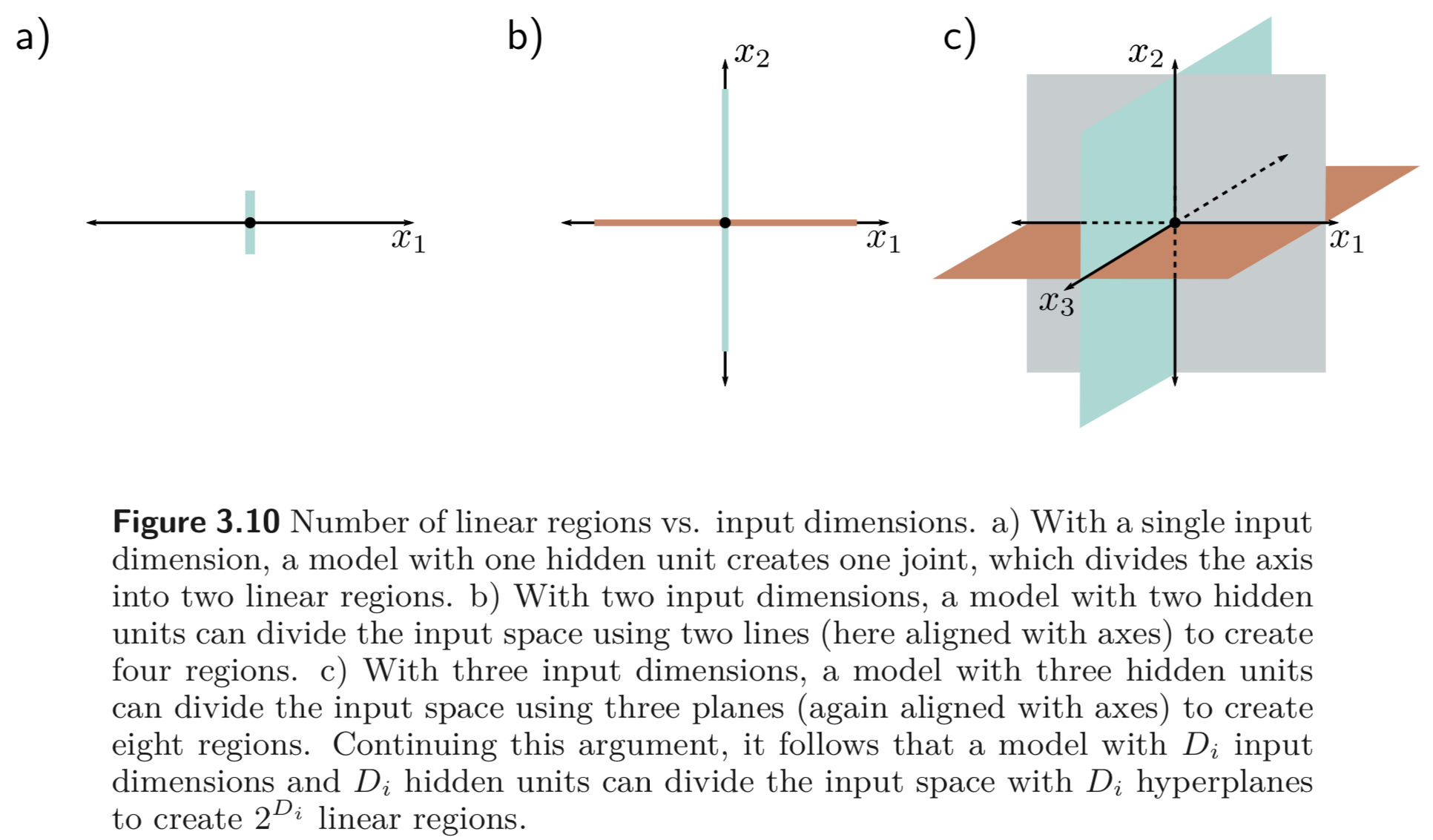
input dimension, # of hidden units이 $2$ 인 경우에는 3.10 b)에 대응할 수 있는데, 이때는 1, 2, 3, 4사분과 같이 4개의 linear regions이 생긴다. 또 input dimension, # of hidden units가 $3$인 경우에는 3.10 c)를 보면, 총 8개의 공간으로 나뉘는 것을 볼 수 있다.

shallow neural network 에서는 hidden units의 갯수가 input dimension, $D_i$ 보다 크므로, shallow neural network 는 보통 못해도 $2^{D_i}$ 이상의 linear regions 를 만들어낸다.

3.4. Shallow Neural Networks: General Case

앞서 shallow neural network이 어떻게 동작하는지에 대한 intuition을 위해 위의 여러 예제들을 살펴보았다. 이제는 multidimension input, output, $\bold{x} \in \R^{D_i}, \bold{y} \in \R^{D_o}$ 를 맵핑하고, hidden units, $\bold{h} \in \R^{D}$ 를 갖는, 일반적인 shallow neural network, $\bold{y=f[x, \phi]}$ 를 정의한다. 각 hidden units는 아래와 같이 계산된다.

$$h_d = a\bigg[ \theta_{d0}+\displaystyle\sum_{i=1}^{D_i}\theta_{di}x_i \bigg]$$

최종 output, $\bold{y}$의 각 elements는 아래와 같이 계산된다.

$$y_j=\phi_{j0} + \displaystyle\sum_{d=1}^{D}\phi_{jd}h_d$$

activation function은 입력/출력의 관계의 nonlinear relation 을 나타내기 때문에, 반드시 nonlinear 한 함수여야한다. 만약 nonlinear relation이 없다면 linear_function(linear_funtion) = linear_function 이므로 모든 관계가 그냥 linear 관계만을 나타낸다.

많은 activation functions이 있지만 ReLU를 선택한 이유는 “쉬워서”이다. 또한 이러한 ReLU function을 통해 모델은 input space를 clip된 hyperplance로 정의된 convex polytopes(복수) 로 나눌 수 있다.

각 convex polytope는 각기 다른 linear function을 포함한다. polytopes는 각 출력에 대해 동일 (”joints”) 하지만, 이들이 포함하는 linear functions는 각기 다를 수 있다.

3.5. Terminology

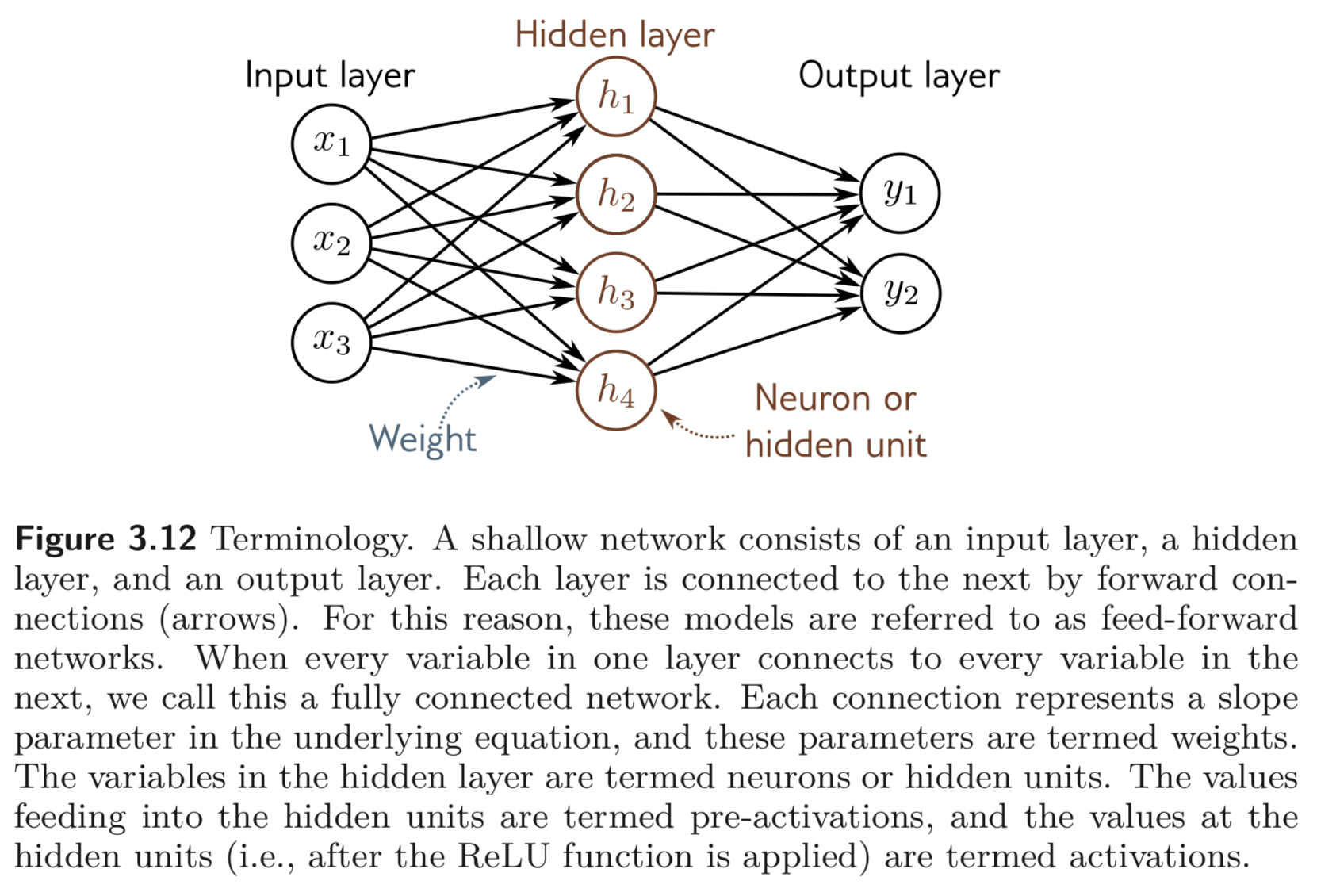
위와 같은 shallow neural network 를 multi-layered perceptron, MLP for brevity. fully-connected layer, FC layer. 라고도 한다.

Hidden layer가 많아진걸 우리는 Deep neural network 라고 하고, acyclic 한 graph로 볼 수 있기 때문에, feed-forward networks라는 표현을 사용한다.

각 파라미터는 weights 라는 표현을 사용하고, offset으로 표현한 것은 bias 라는 term 을 사용한다.

3.6. Summary - Take home

1. Shallow neural network는 하나의 hidden layer를 갖는다. 이는 1) input에 대하여 여러 linear function을 계산하고, 2) activation function에 이를 feed 한다. 3) 이러한 activations를 가지고 linear combination 하여 최종 output을 계산한다.

2. Shallow neural network는 input, $\bold{x}$에 기반하여 input space를 piecewise linear regions의 continuous space로 나누어 output, $\bold{y}$를 계산한다.

3. shallw neural network는 충분한 갯수의 hidden units가 있다면 임의의 정확도를 갖는 어떠한 continuous function이라도 이를 approximation 할 수있다. [Universal Approximation Theorem]

Problems

• 3.1. Equation 3.1. (첫번째 식)에서 만약 activation function이 $a[z] = \psi_0 + \psi_1z$ 거나, $a[z]=z$ 라면 어떤 input, output 간의 mapping이 생성될까?
  • hyperplane, 정리하면, 그냥 linear function이 나옴.

• 3.2. 오른쪽 figure 에서 어떤 hidden units이 active 되고 inactive 되었는가?
  • $h_1, h_3$: active, $h_2$: inactive

• 3.3. Figure. 3.3. j. 에 나타난 식을 10개의 파라미터와 input $x$ 에 대해서 “joints”의 위치를 나타내는 식으로 유도하라. 4개의 linear regions의 기울기를 구하는 식을 유도하라.
  • joints

    

  • slopes

    

Uploaded by N2T