Deep Neural Network

본 포스팅은 Simon J.D. Prince 의 Deep Learning 교재를 스터디하며 정리한 글임을 밝힙니다.

https://udlbook.github.io/udlbook/

Take Home

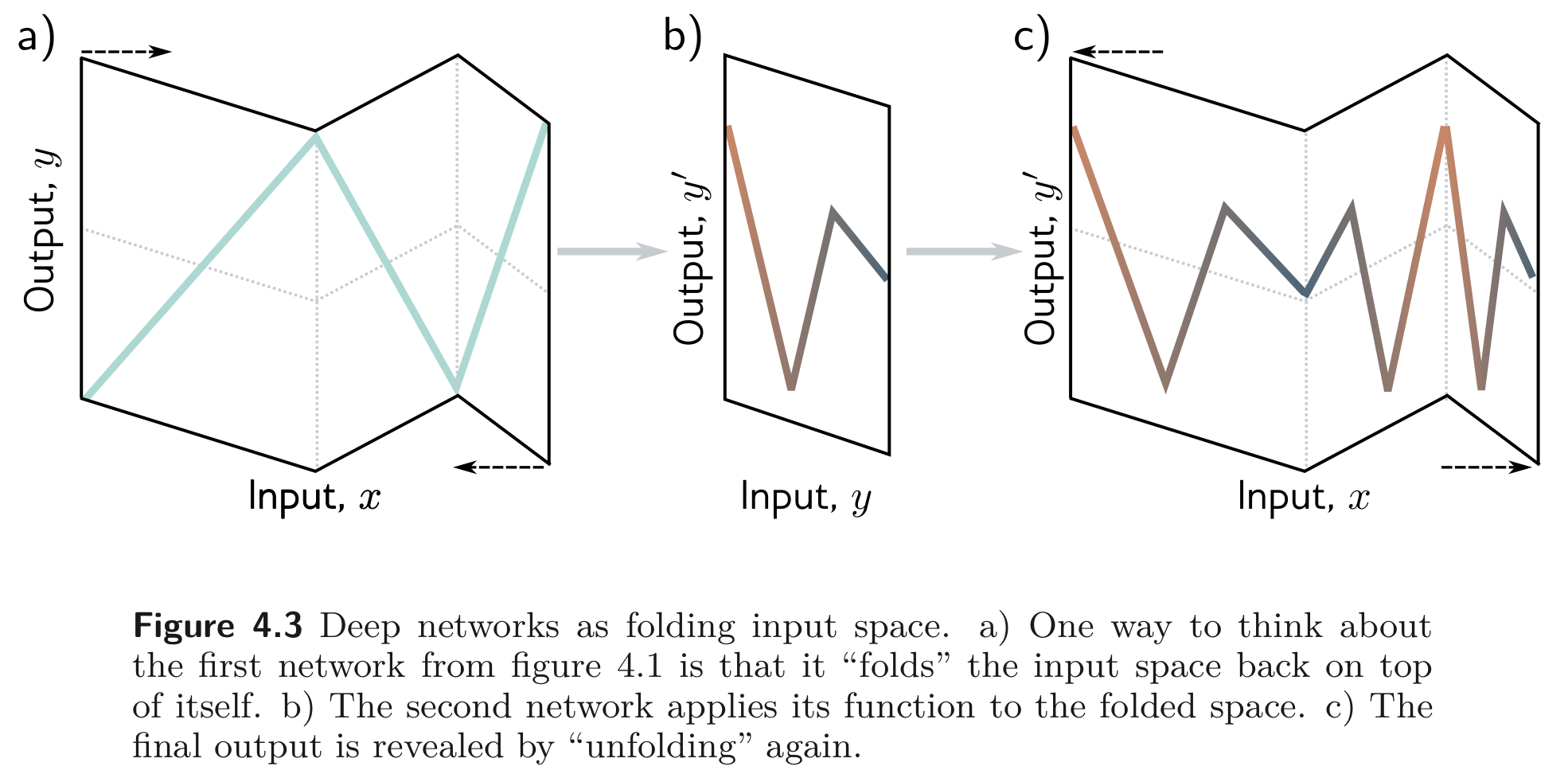
1. 2개의 SNN을 합쳐놓았을 때, 첫 번째 SNN은 input space를 joints 에 따라 folds 함. 두 번째 SNN은 piece wise linear function (linear transformation) 을 적용하는데 두 번째 SNN을 통과한 함수는 앞서 첫 번째 SNN이 접어놓은 space에 복붙됨.

2. 두 개의 SNN을 붙여놓은 DNN은 사실 2개의 hidden layers를 갖는 DNN으로 표현될 수 있음. ReLU activation은 입력을 clipping 하여 새로운 “joints” 를 추가한다.

3. SNN과 DNN을 비교하였다. 1) SNN, DNN 모두 충분한 capacity가 주어진다면 임의의 함수를 근사할 수 있고, 2) DNN은 같은 파라미터의 수로 훨씬 많은 linear regions를 만들어내며, 3) 어떤 함수들은 DNN으로 훨씬 효율적으로 나타낼 수 있다. 4) large, structured input에 대해서는 multi-layer를 갖는 network로 처리해야하며, 5) 실제로는 SNN보다 DNN이 대부분의 tasks 에서 SOTA를 달성하였다. 이유는 모르겠지만.

---

지난 챕터에서는 하나의 hidden layer만을 갖는 shallow neural networks (이하 SNN)를 다룸. 이번 챕터는 2개 이상의 hidden layer를 갖는 deep neural network (이하 DNN) 를 다룸. ReLU activation function 을 통해 shallow, neep neural networks는 input과 output 사이의 관계를 piecewise linear mapping으로 나타낸다.

hidden units의 수가 늘어날 수록, SNN은 표현력 (descriptive power)가 증가했다. 그리고 hidden units이 충분하면 이는 임의의 복잡한 고차원 함수를 나타낼 수 있다. 하지만 어떤 함수에 대해서는 필요한 hidden units의 수가 말도 안되게 증가한다. DNN은 같은 수의 파라미터를 가지고도 SNN 보다 더 많은 linear regions를 표현할 수 있다. 실용적인 측면에서, DNN은 더 다양한 family of functions을 표현할 수 있다.

4.1. Composing Neural Networks

DNN의 동작 원리를 이해하기 위해 두 개의 SNN을 첫 번째 SNN의 출력이 두 번째 SNN의 입력이 되도록 하는 2개의 SNN들로 합친다.

Figure 4.1.

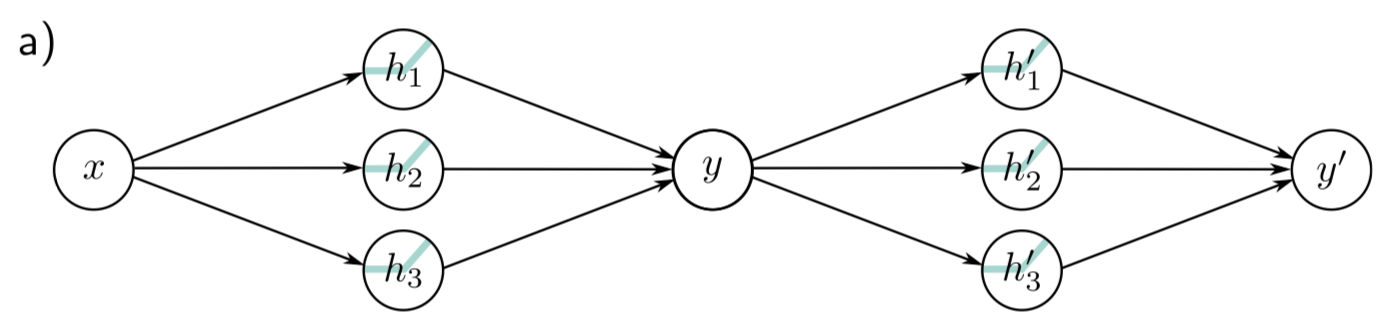
각 SNN은 3개의 hidden units를 갖는다고 하자. 첫번째 SNN은 아래와 같이 정의된다.:

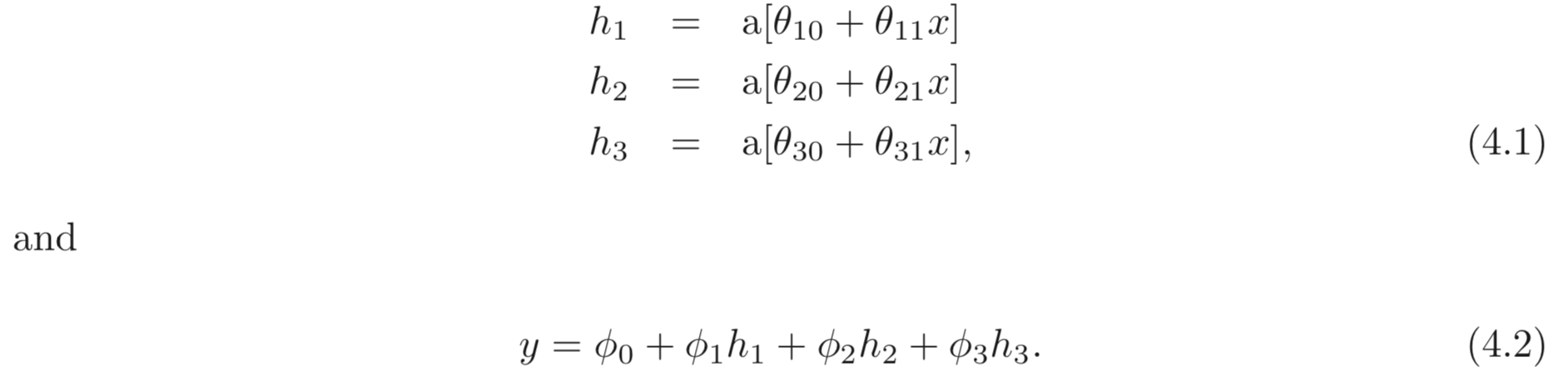
두 번째 SNN은 아래와 같이 정의된다.

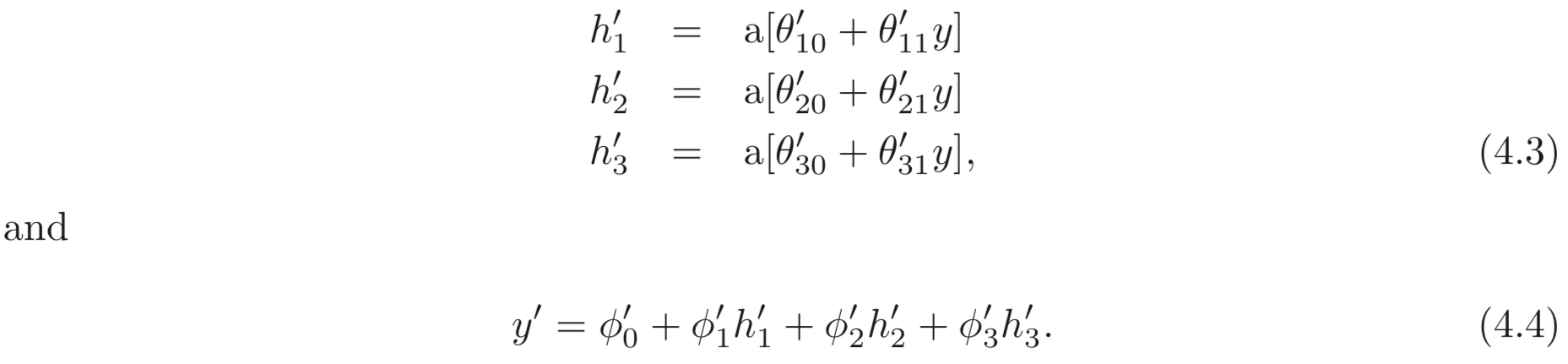
ReLU activation을 사용하기 때문에 두 SNN으로 정의한 DNN 모델은 family of piecewise linear functions을 나타낸다. 하지만 이렇게 표현된 모델의 linear regions의 수는 6개의 hidden units을 갖는 하나의 SNN보다 훨씬 많을 수 있다. 이를 보이기 위해 첫 번째 SNN 을 교대로 양수, 음수, 양수의 기울기를 갖는 regions로 생각해보자.

Figure 4.1.

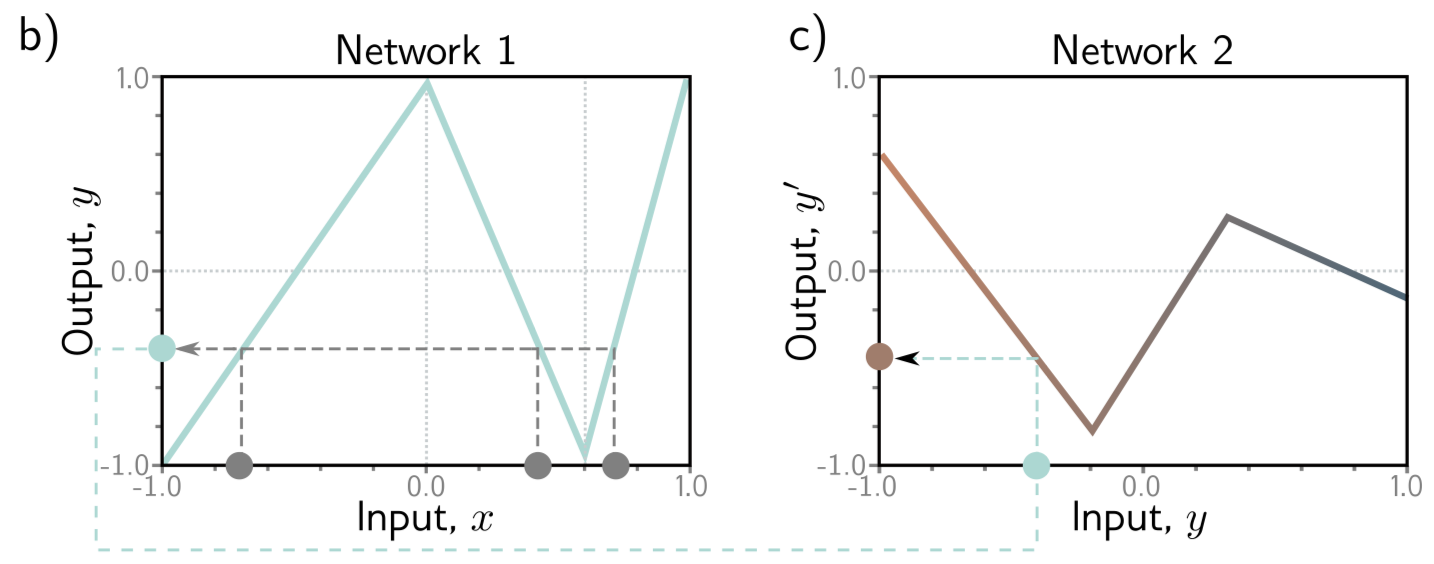
(간단하게 예를 들기 위해 모든 공간을 $[-1,1]$ 에서만 고려한다.) Figure 4.1. b)를 보면 3개의 linear regions으로 나타나있고, 각 linear regions가 갖는 range에 속한 $x$는 각각 $y \in [-1,1]$ 로 맵핑된다. 그리고 $y$는 두 번째 SNN에서 정의된 함수처럼 $y \rightarrow y'$ 으로 맵핑된다.

정리하자면, 첫 번째 SNN은 아래와 같이 나타낼 수 있다. 3개의 맵핑으로 표현될 수 있다.

$$\begin{align} x_1 \in [-1, 0] &\rightarrow y \in [-1, 1]\\ x_2 \in [0, 0.6] &\rightarrow y \in [-1, 1]\\ x_3 \in [0.6, 1] &\rightarrow y \in [-1, 1] \end{align}$$

두 번째 SNN은 $y \in [-1, 1] \rightarrow y'$(Figure 4.1. c) 을 맵핑하므로 두 SNN을 합친 DNN은 $[-1, 1]$ 범위에서 총 3개의 (적절한 값의 weight로 곱해진) Figure 4.1. c)와 같은 함수 모양을 볼 수 있다.

Figure 4.1.

즉, 첫 번째 SNN은 “input space $x$를 그 위에 다시 접는다.” (fold input space $x$ back onto itself) 라고 생각할 수 있다.

4.2. From Composing Networks to Deep Networks

이전 섹션에서 첫 번째 SNN의 출력을 두 번째 SNN에 넘기는 벙법으로 복잡한 함수를 합성할 수 있다는 것을 봤다. 본 섹션에서는 앞 선 예제가 2개의 hidden layers를 갖는 특별한 케이스임을 보인다. (3개 아님? 아님. 뒤에서 설명)

첫 번째 SNN의 출력 ($y = \phi_0 + \phi_1h_1 + \phi_2h_2 + \phi_3h_3$) 과 두 번째 SNN의 첫번째 연산들 ($h'_i = a[\theta'_{i0} + \theta'_{i1}y]$)은 둘 다 linear 하다. linear function을 다른 linear function에 넘기면 linear function을 갖는다 (yields). 즉, 두 나누어진 식을 하나의 linear 식으로 나타내는 것이 가능하다.

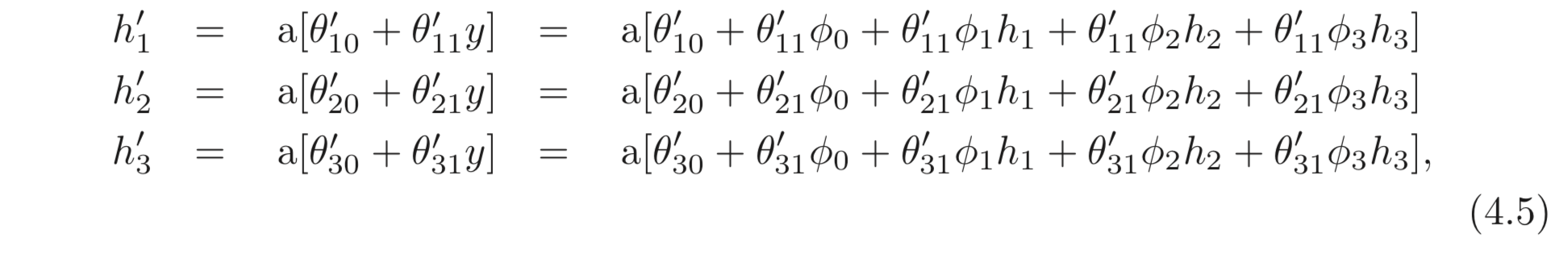
따라서, $y$에 대한 식을 빼고 이를 합치면 두 번째 SNN의 hidden units를 아래와 같이 나타낼 수 있다.

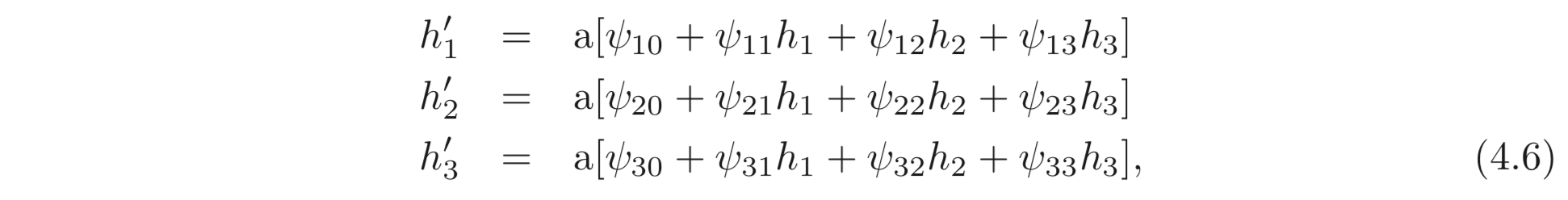
$\text{where, } \psi_{10} = \theta'_{10} + \theta'_{11}\phi_0 \text{ and so on.}$ 앞 선 두 개의 SNN을 붙인 DNN은 아래와 같이 표현된다.

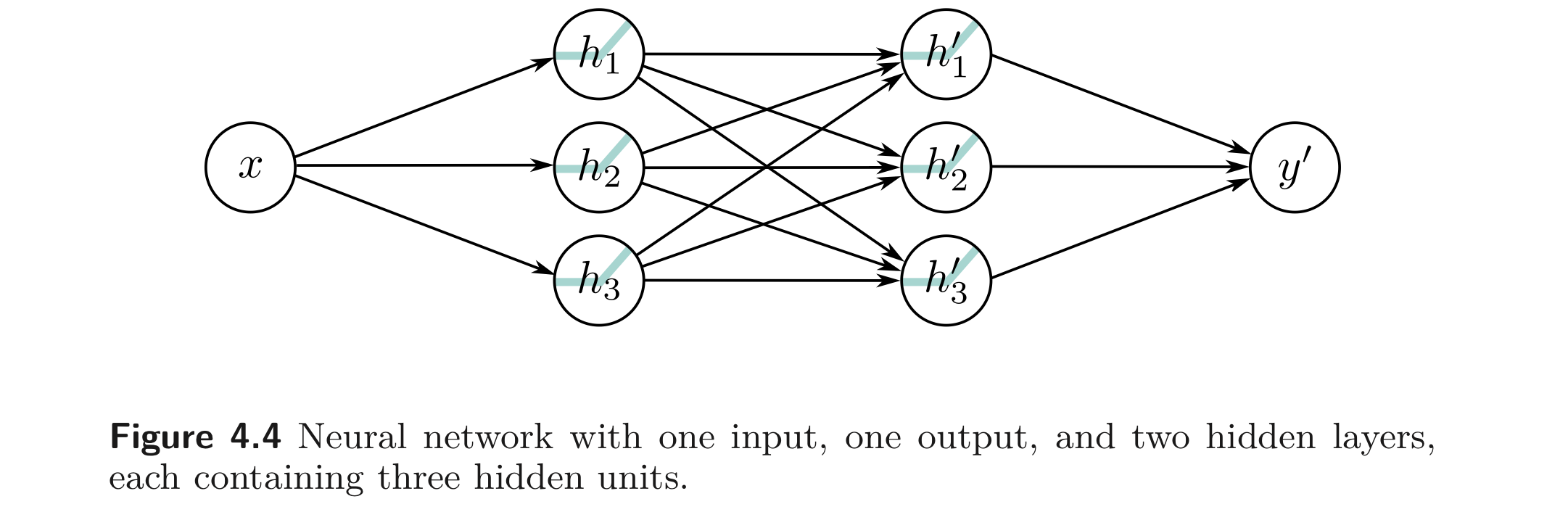
또 다른 사실은, Equation 4.6의 식 (Figure 4.4 와 같은 구조) 은 총 9개의 기울기 값이 임의의 값을 가질 수 있으므로 더 다양한 함수를 나타낼 수 있다. 반면, Equation 4.5는 $[\theta'_{11}, \theta'_{21}, \theta'_{31}]^T[\phi_1, \phi_2, \phi_3]$ 의 외적 값으로 계산되므로 더 제한적이다.

4.3. Deep Neural Networks

앞서 두 개의 SNN을 붙여 만든 모델은 특별한 case의 DNN이라는 것을 보았다. 본 섹션에서는 3개의 hidden units을 갖고 2개의 hidden layers를 갖는 일반적인 case의 DNN을 살펴 본다. 아래와 같이 정의됨.:

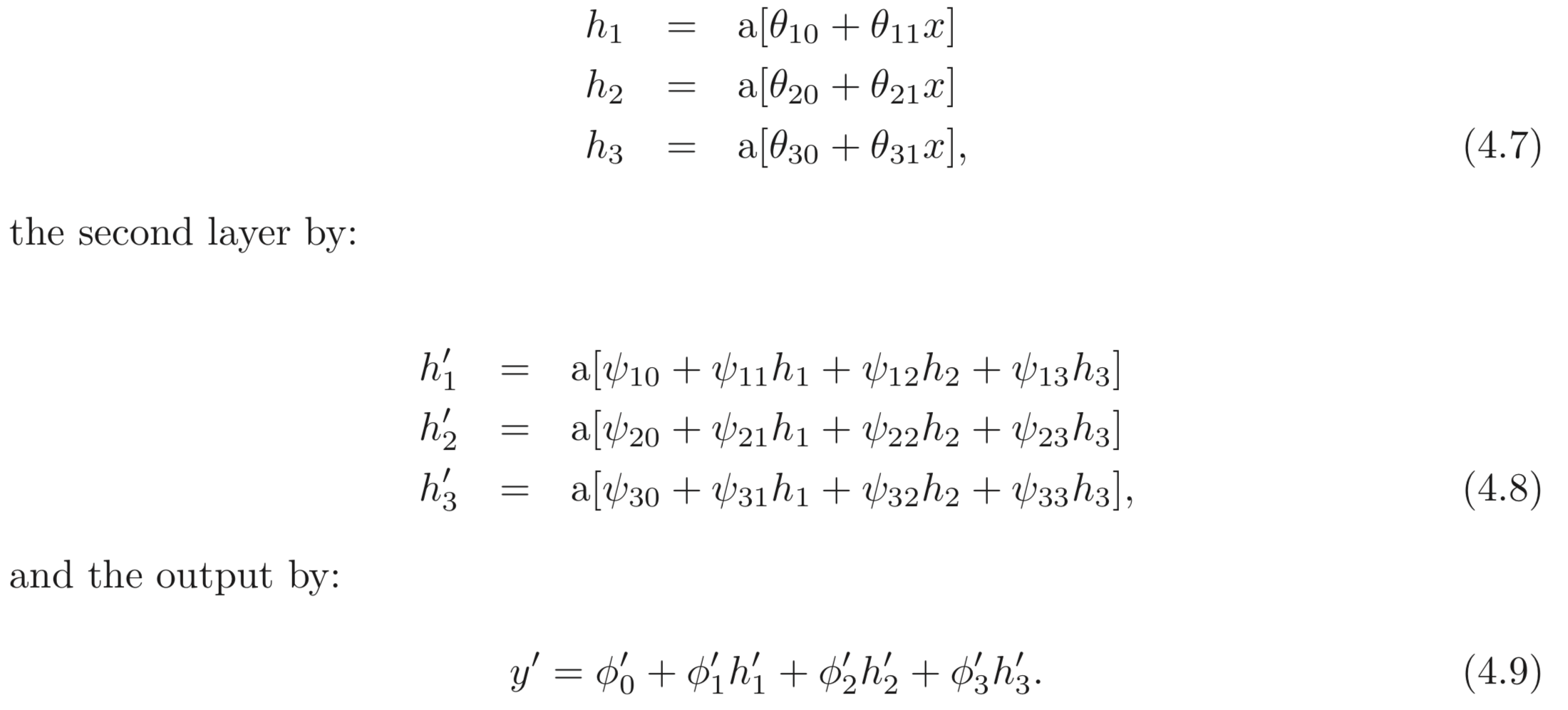
위 식을 잘 살펴보면 모델이 어떻게 복잡한 함수를 나타내는지 알 수 있다. 이들의 중간값들이 그리는 그래프는 아래와 같이 나타낼 수 있다.

Figure 4.5. a-c)는 h1, h2, h3에 의해 만들어지기 때문에 모두 같은 “joint” points를 갖는다.

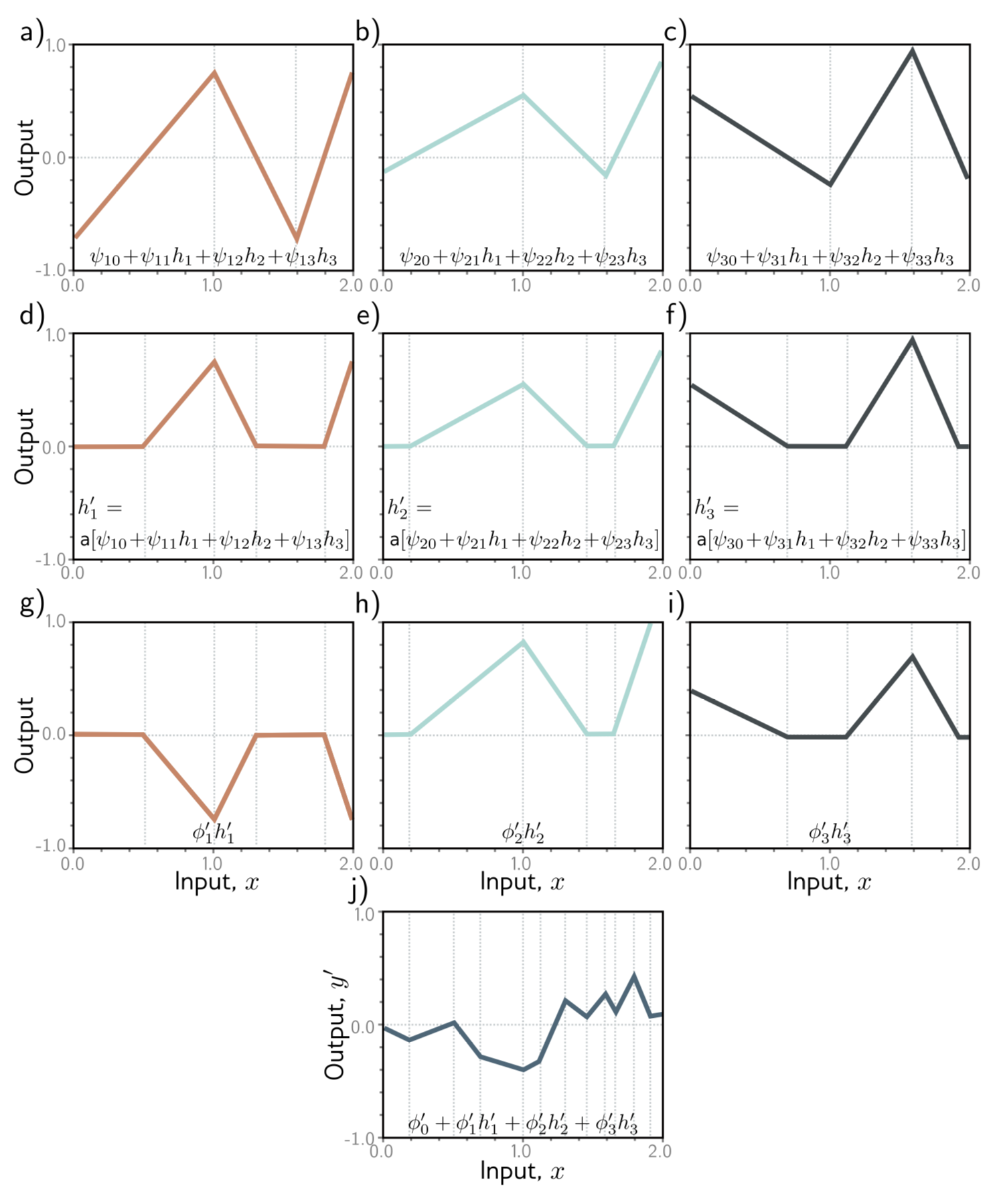
1. 3개의 hidden units, $h_1, h_2, h_3$ 가 linear function을 지나 ReLU를 거쳐 만들어진다. (Eq. 4.8)

2. pre-activations는 $h_1, h_2, h_3$ 를 linear function에 넣음으로 구할 수 있다 (Eq. 4.8). 그리고 이들은 기울기는 다르지만 모두 같은 “joint” points를 갖는다. (Figure 4.5 a-c))

3. 두 번째 hidden layer 에서는 다른 ReLU가 앞선 계산 결과들을 clip 하여 새로운 joints를 추가한다. (Fig. 4.5 d-f))

4. 최종 결과는 이들의 결과를 linear combination 한 결과이다. (Fig. 4.5 j))

정리하자면, 우리는 각 layers를 input space를 접거나 (folding) clip되고 결합되는 새로운 함수를 합성하는 것 (createing new functinos)으로 생각할 수 있다.

전자는 출력 함수에 대한 의존성을 강조하지만, clipping이 (ReLU) 어떻게 joints를 만드는지는 알 수 없고 후자는 반대이다. 두 표현 모두 부분적으로만 나타내므로 둘 다 이해하고 있는 것이 중요.

4.3.1 Hyperparameters

보통 DNN은 엄청나게 많은 hidden layers, hidden units를 가짐. hidden units의 수를 width 라고 하고 hidden layers의 수를 depth 라고 하며 hidden units의 총 갯수를 network의 capacity 라고 한다.

$K$ 개의 hidden layers에 각 layer의 hidden units의 수를 $D_1, D_2, ..., D_K$ 라고 하자. 이때 이러한 값들을 Hyperparameter의 일부 라고 볼 수 있다.

Hyperparameters에 따른 DNN 예시는 아래와 같다.

Figure 4.6

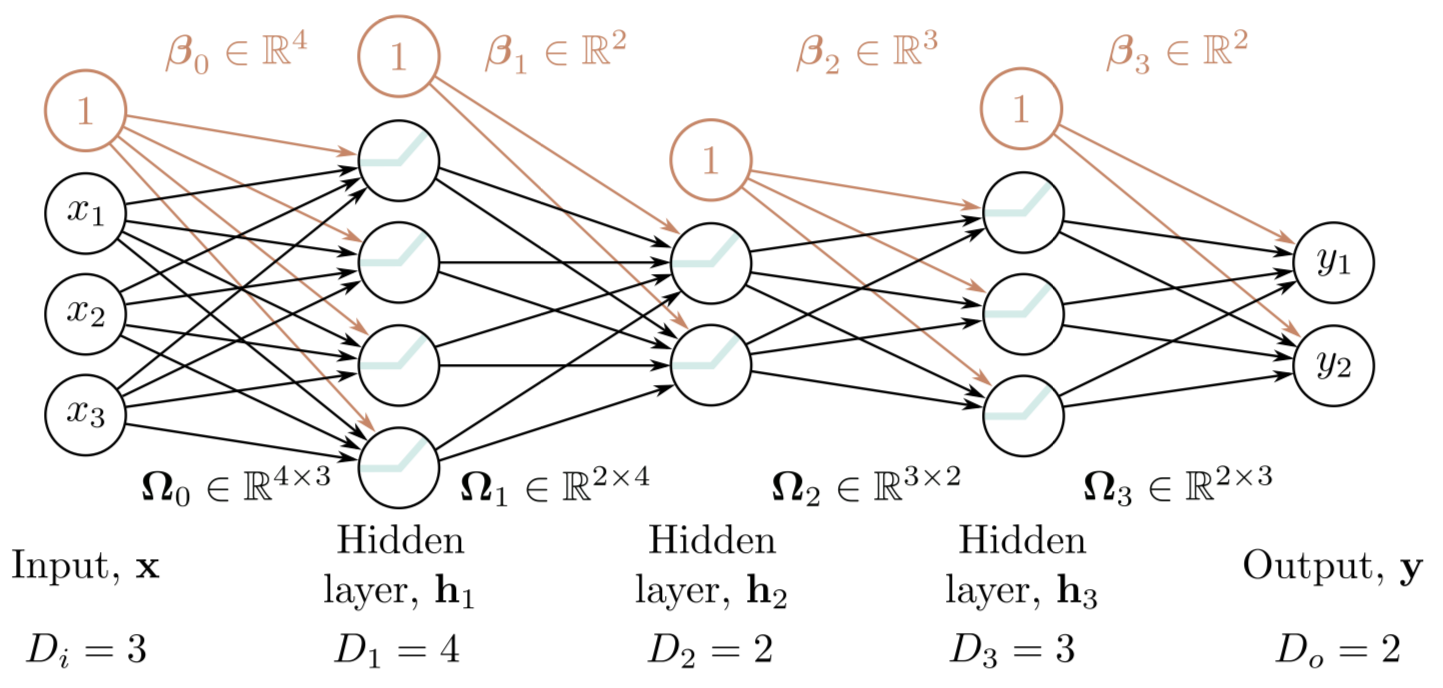
4.4 Matrix Notation

앞서 DNN이 linear transformation과 activation function이 교대로 포함돼있다는 것을 보았다. 앞선 식, Eq. 4.7-4.9는 아래와 같이 matrix notation으로 나타낼 수 있다.

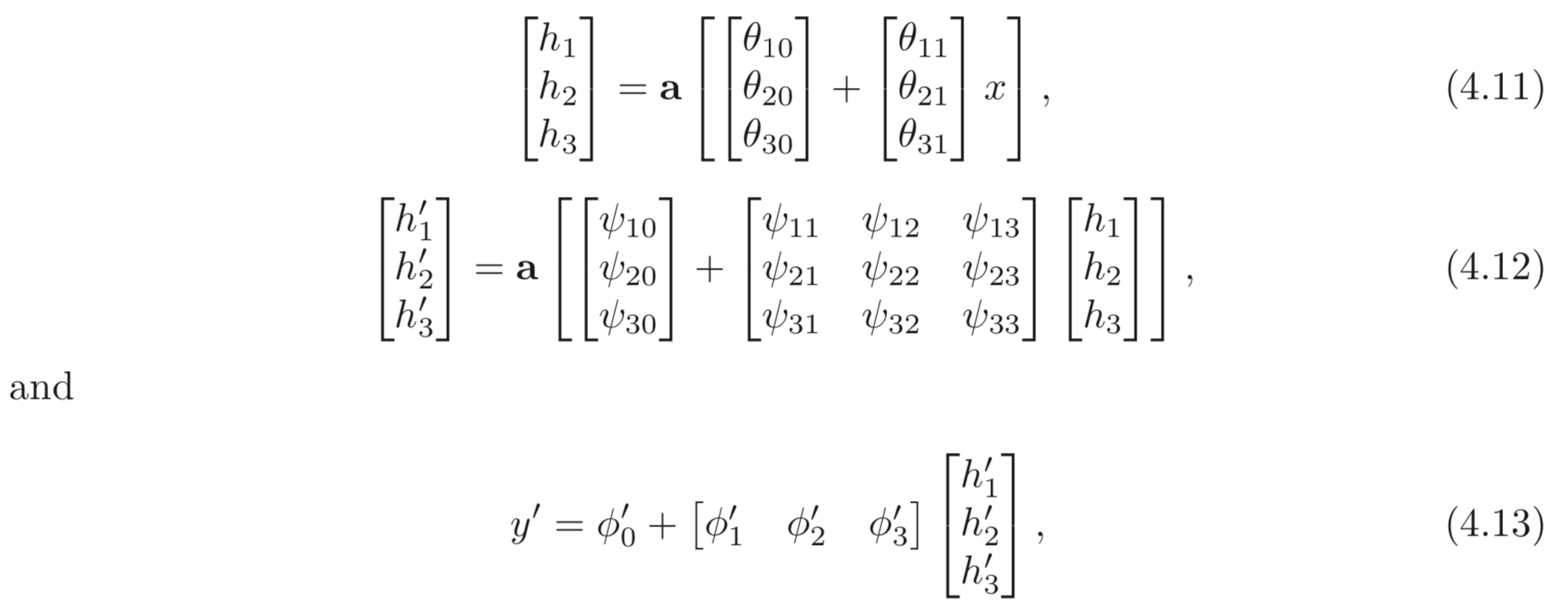
혹은 더 컴팩트하게는 아래와 같이 나타낼 수 있다.

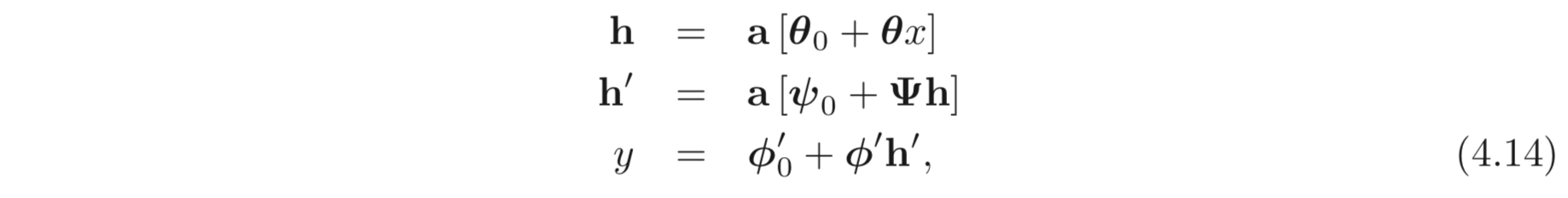
bold체 소문자는 vector, bold체 대문자는 matrix다. activation funciont은 element-wisely 연산된다.

4.4.1 General Formulation

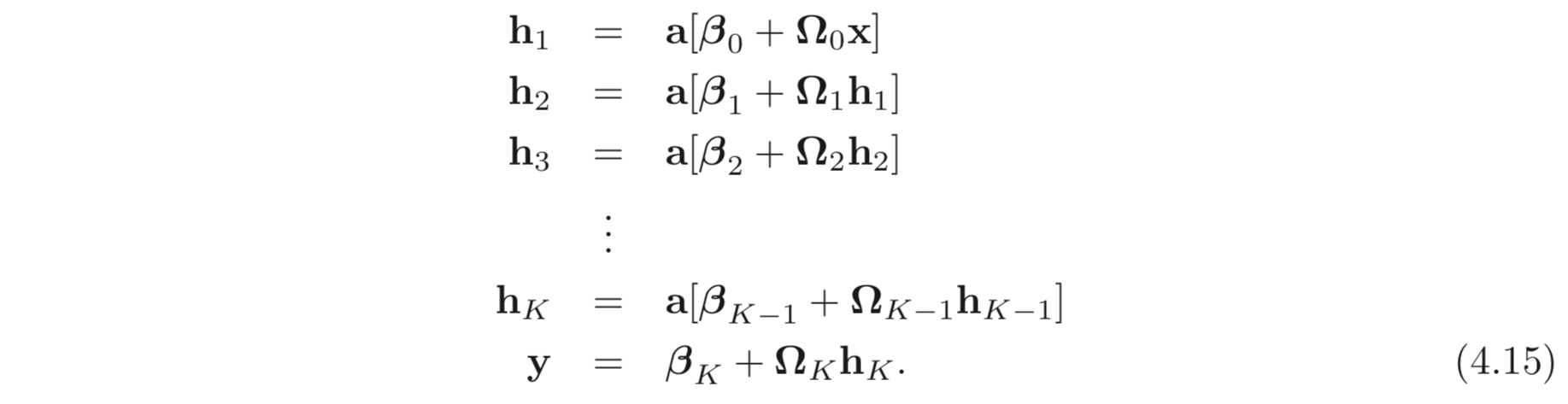
4.5 Shallow vs. Deep Neural Networks

본 섹션에서는 shallow networks 와 deep networks의 차이점을 살펴본다.

4.5.1 Ability to Approximate Different Functions

Chapter 3에서 소개한 Universal Approximation Theorem을 shallow neural network가 임의의 모든 continuous function을 근사할 수 있는 사실에 대해 공부했다. 또한 두 개의 SNN을 합친 것이 사실은 두 개의 hidden layers를 갖는 DNN으로 표현할 수 있는 것에 대해 공부했다. 만약 두 번째 layer가 identity function 이라면, single layer SNN 과 같으므로 모든 함수를 근사할 수 있을 것이다. 흠?

DNN도 모든 함수를 근사할 수 있다.

4.5.2 Number of Linear Regions per Parameter

$D$개의 hidden units을 갖는 SNN은 $D+1$의 linear regions를 만들고, $3D+1$ 개의 parameters를 갖는다. $K$개의 hidden layers, $D$개의 hidden units를 갖는 DNN은 $(D+1)^K$ 개의 linear regions를 가지며, $3D+1+(K-1)D(D+1)$ 개의 parameters를 갖는다.

DNN은 depth, $K$ 에 대하여 linear regions의 수가 exponentially 증가한다.

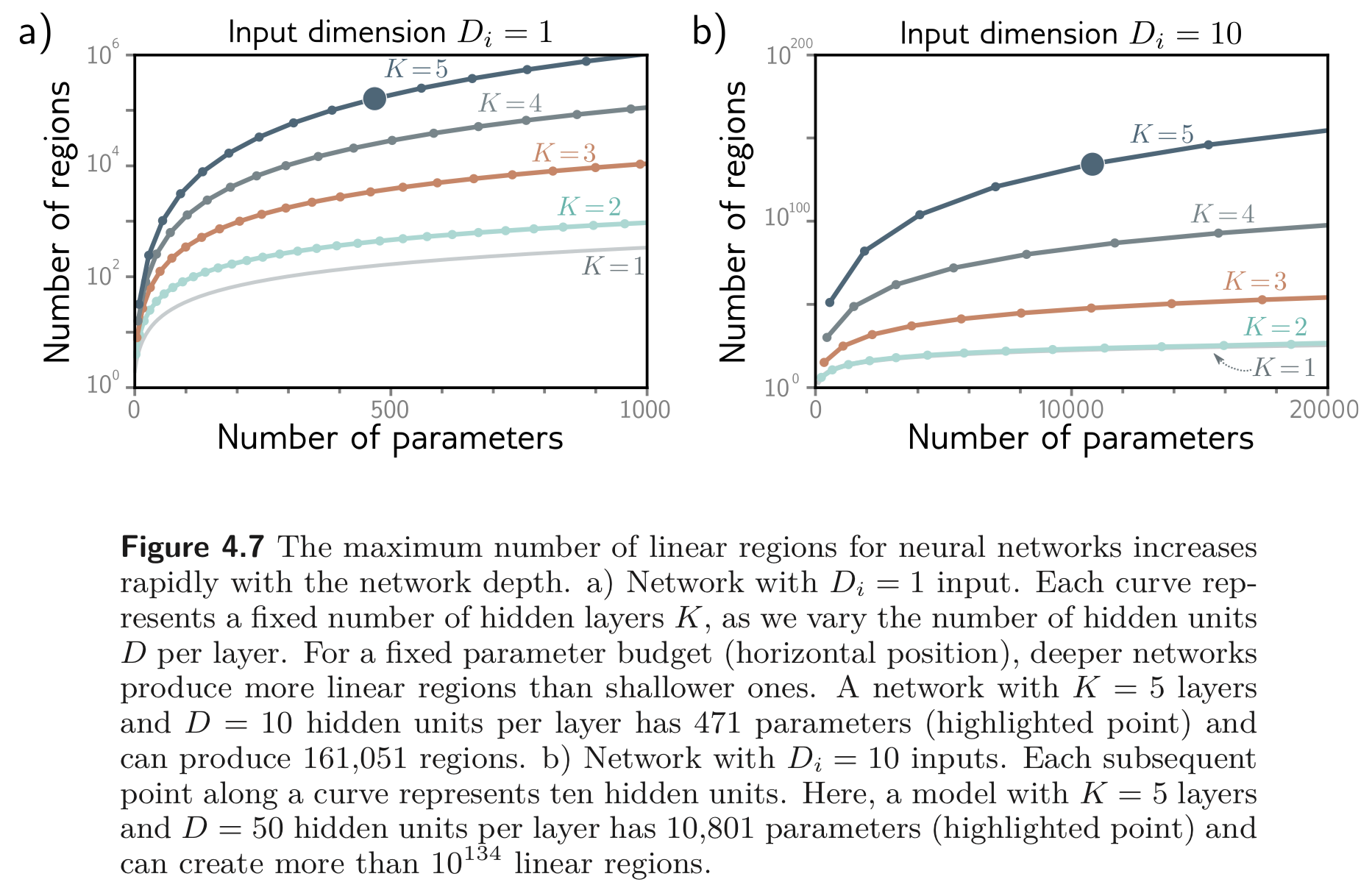
linear regions가 많아질수록 임의의 함수에 근사할 수 있으므로 이는 굉장히 매력적으로 느껴질 수 있겠지만, 함수의 유연성은 여전히 파라미터의 수에 의존한다. DNN은 엄청나게 많은 수의 linear regions를 만들 수 있지만, 여기에는 복잡한 의존성과 대칭들이 있다 (최종적으로 만들어진 함수는 하나의 linear combination 함수를 적절한 weight를 곱하여 더한 것이기 때문임 “folding”).

따라서 DNN으로 만들어진 엄청나게 많은 linear regions가 advantage를 가지려면 다음과 같은 사실이 있어여한다.

1. 우리가 근사하고자 하는 현실 세계의 함수에 비슷한 대칭성이 있어야한다.

2. 입력과 출력 사이의 맵핑이 실제로 더 간단한 함수들로만 이루어져 있어야한다.

따라서 depth를 늘려서 얻은 linear regions이 더 완벽한 임의의 함수를 근사할거라고 기대해서는 안됨.

4.5.3 Depth Efficiency

앞서 같은 linear regions를 얻기 위해 SNN은 DNN에 비해 파라미터의 수를 exponentially 증가시켜야했다. 따라서 DNN이 더 적은 수의 파라미터로도 임의의 함수를 근사할 수 있다고 여길 수 있는데 이를 depth efficiency 라고 한다.

이는 역시 매력적이지만 real-world 예제에서도 이가 맞아 떨어질거라고는 기대하지 마라.

4.5.4 Large and Structured Inputs

앞선 예제에서는 모두 FC network에 대해서만 살펴보았는데, 하지만 이미지 같은 large, structured 입력에 대해서는 FC network는 적합하지 않다. 이미지는 약 $10^6$ 정도의 픽셀을 갖는데 이러한 크기의 입력을 FC layer로 처리하는 것은 해서는 안된다.. (prohibitive) 그리고 이미지 같은 경우에는 한 장의 이미지에서 여러 object를 찾는 등 다른 해상도를 갖는 이미지에 대해서도 같은 연산을 수행했으면 하는 바램이 있다.

이는 이미지의 local regions을 병렬적으로 처리하고, 점점 global regions에 integration 하는 방법이 있다. 이러한 종류의 local-to-global processing (CNN) 은 multiple layers가 없으면 나타내기 어렵다.

4.5.5 Training and Generalization

DNN이 SNN보다 이점을 갖는 다른 부분은 학습이 더 쉽다는 점에 있다. 적당히 깊은 DNN이 보통 SNN보다 학습이 쉽다.

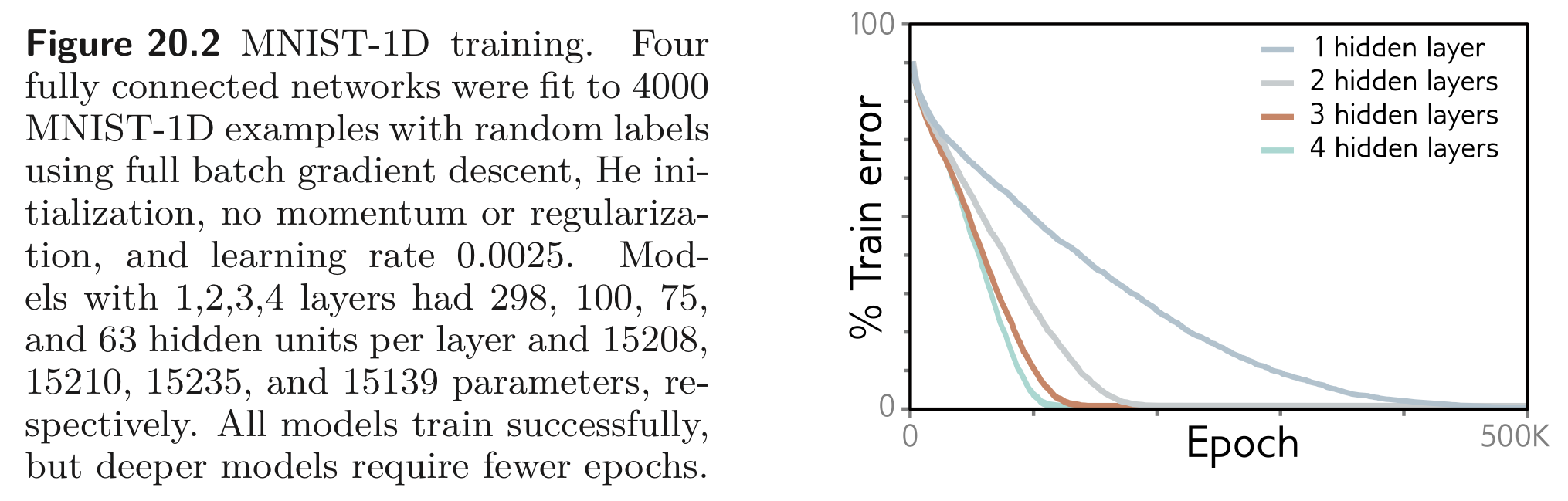
하지만, 뒤에서 공부하겠지만 (Chapter11 Residual networks) depth가 깊어질 수록 학습하기 어려워진다. 그럼에도 불구하고 DNN은 SNN보다 새로운 데이터를 잘 generalize 하는 것으로 보인다. 실질적으로 대부분의 task들의 가장 좋은 결과는 수십에서 수백개의 layers를 갖는 DNN으로 얻어진다.

상충되어 보이는 두 현상들 (1. layers가 깊어진다고 좋은 결과를 얻는 것은 아님. 2. 근데 깊으면 잘함 ㅋ) 은 아직 잘 이해되지 않은 부분들이다.

4.6 Summary

1. 앞서 2개의 SNN을 합쳐놓았을 때 어떻게 동작하는지 공부했다. 첫 번째 SNN은 input space를 joints 에 따라 접었고, 두 번째 SNN은 piece wise linear function을 적용하는데 두 번째 SNN을 통과한 함수는 앞서 첫 번째 SNN이 접어놓은 space에 복붙된다.

2. 그리고 두 개의 SNN을 붙여놓은 DNN은 사실 2개의 hidden layers를 갖는 DNN으로 표현될 수 있음을 공부했고, ReLU activation은 입력을 clipping 하여 새로운 “joints” 를 추가한다는 점을 보았다.

3. 마지막으로 SNN과 DNN을 비교하였다. 1) SNN, DNN 모두 충분한 capacity가 주어진다면 임의의 함수를 근사할 수 있고, 2) DNN은 같은 파라미터의 수로 훨씬 많은 linear regions를 만들어내며, 3) 어떤 함수들은 DNN으로 훨씬 효율적으로 나타낼 수 있다. 4) large, structured input에 대해서는 multi-layer를 갖는 network로 처리해야하며, 5) 실제로는 SNN보다 DNN이 대부분의 tasks 에서 SOTA를 달성하였다. 이유는 모르겠지만.

Uploaded by N2T